Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция - семинар Сетевое планирование и управление
Содержание
- 1. Лекция - семинар Сетевое планирование и управление
- 2. Теоретические сведения о сетевом планировании и управлении
- 3. Теоретические сведения о сетевом планировании и управлении
- 4. Этапы построения сетевого графика Сетевое Планирование и Управление
- 5. Понятия, используемые в сетевых моделях Основными понятиями сетевых
- 6. Понятие: работа По своей физической природе работы можно
- 7. Сетевой график Взаимосвязь работ и событий, необходимых для
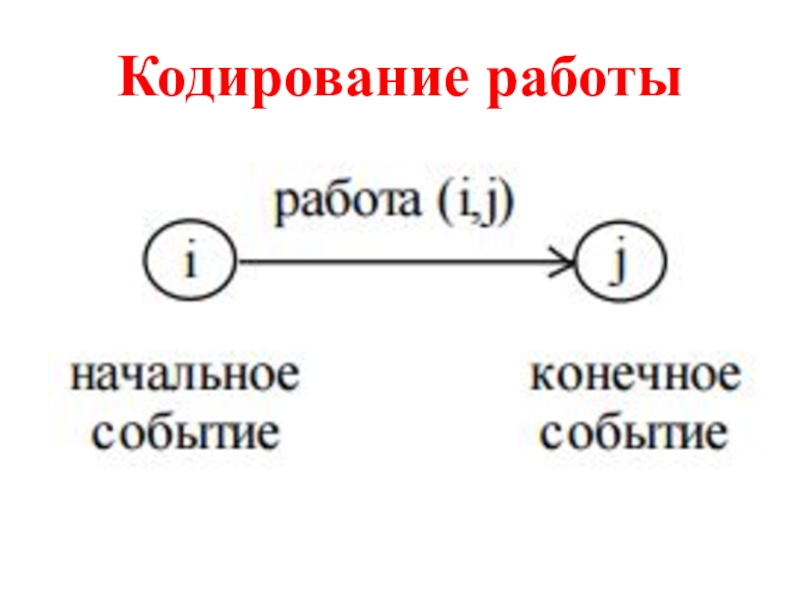
- 8. Кодирование работы
- 9. «Событие» в сетевом графике Любое событие может считаться
- 10. Правила построения сетевого графика (1) 1. Длина стрелки
- 11. Правила построения сетевого графика (2) 7. Не
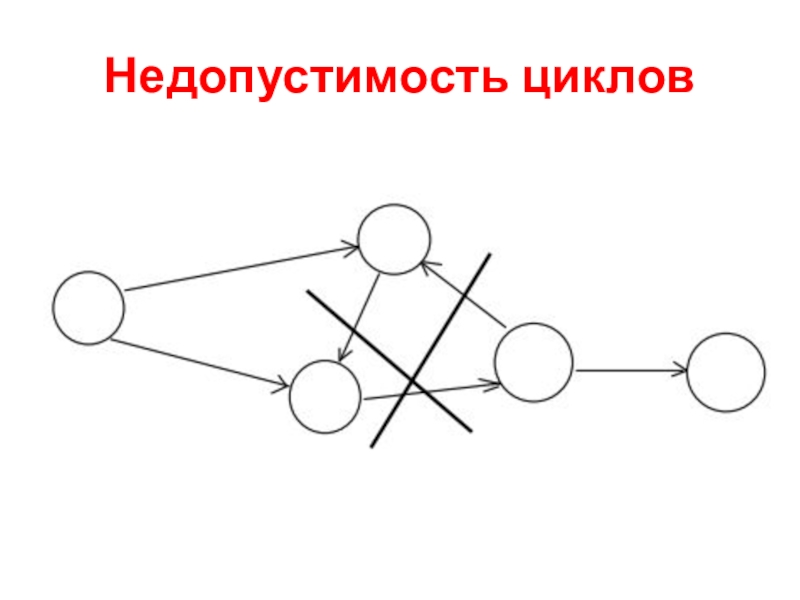
- 12. Недопустимость циклов
- 13. Параметры сетевого графика (понятие пути) Важное значение для
- 14. Параметры сетевого графика (временные характеристики) На основании
- 15. Определение ранних сроков совершения событий - -
- 16. Определение поздних сроков совершения событий- срок совершения
- 17. Определение резерва времени совершения события - резерв
- 18. Представление показателей события на графике Рассчитанные численные значения временных параметров записываются прямо в вершины сетевого графика:
- 19. Определение полного резерва времени работы (1) -
- 20. Определение полного резерва времени работы (2) Важнейшее
- 21. Определение свободного резерва времени работы (1) -
- 22. Определение свободного резерва времени работы (2) Использование
- 23. Анализ сетевого графика с целью последующей его
- 24. КОЭФФИЦИЕНТ НАПРЯЖЁННОСТИ РАБОТ - Кн (i,j) Кн (i,j)
- 25. Числовое значение Кн (i,j) определяется по формуле:
- 26. ОЦЕНКА КОЭФФИЦИЕНТА НАПРЯЖЁННОСТИ РАБОТ - Кн (i,j) Чем
- 27. СОКРАЩЕНИЕ ПРОДОЛЖИТЕЛЬНОСТИ КРИТИЧЕСКОГО ПУТИ Продолжительность критического пути может
- 28. КЛАССИФИКАЦИЯ КОЭФФИЦИЕНТОВ НАПРЯЖЁННОСТИ РАБОТ - Кн (i,j) Вычисленные
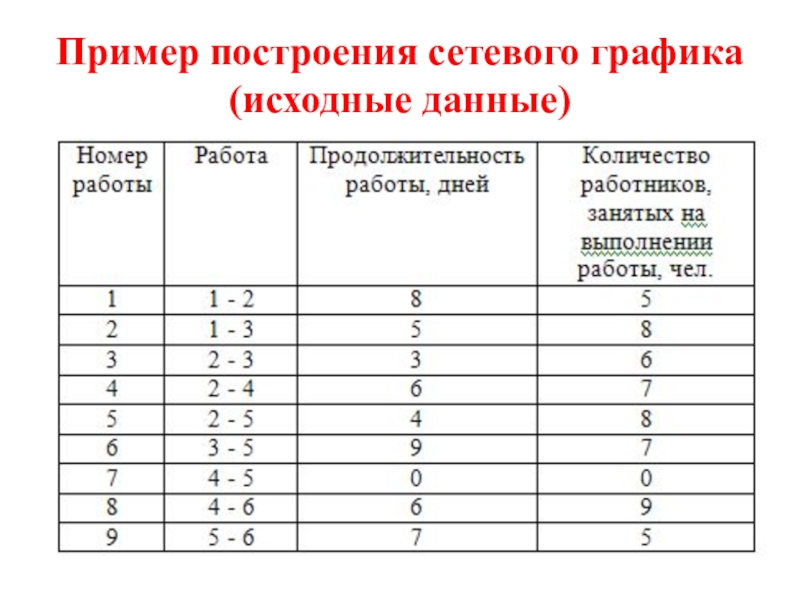
- 29. Пример построения сетевого графика (исходные данные)
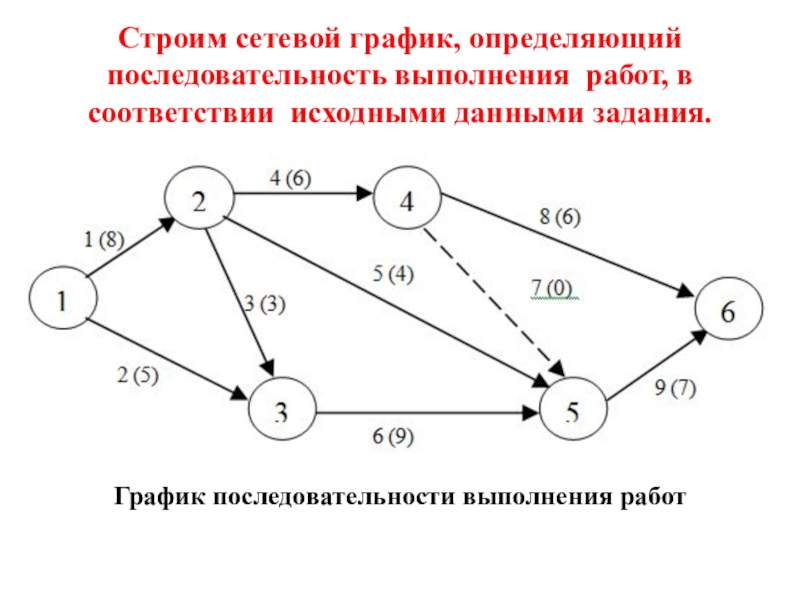
- 30. Строим сетевой график, определяющий последовательность выполнения
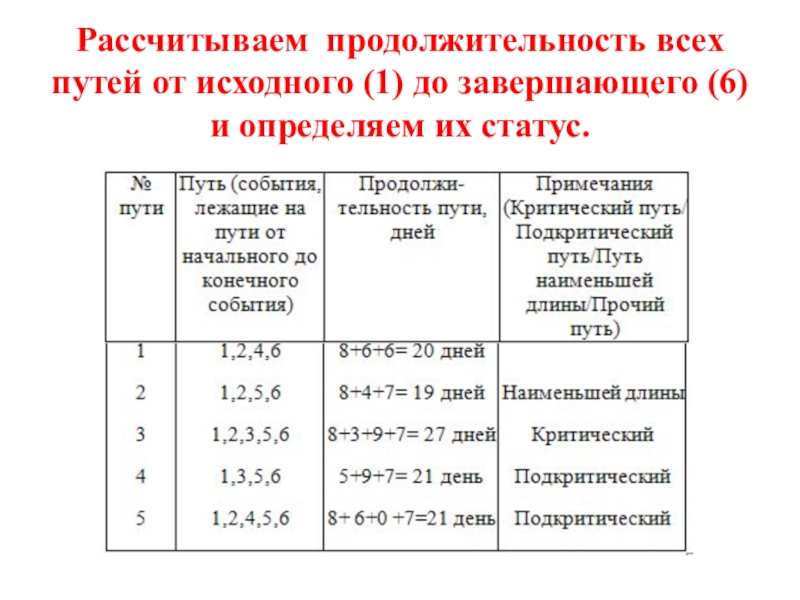
- 31. Рассчитываем продолжительность всех путей от исходного (1) до завершающего (6) и определяем их статус.
- 32. Рассчитываем параметры сетевого графика и строим
- 33. Поздние сроки совершения событий (1)
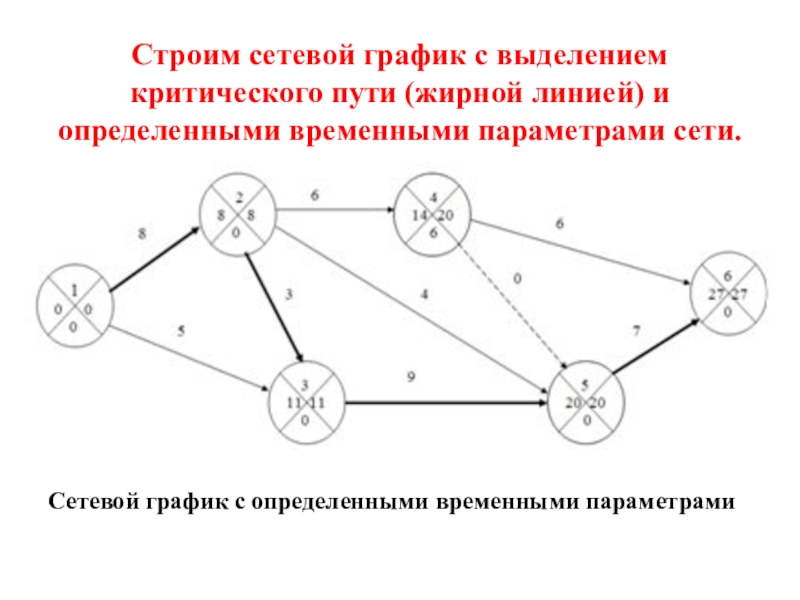
- 34. Строим сетевой график с выделением
- 35. Рассчитываем остальные параметры сетевого графика: резерв времени событий, Полный и свободный резервы времени работ
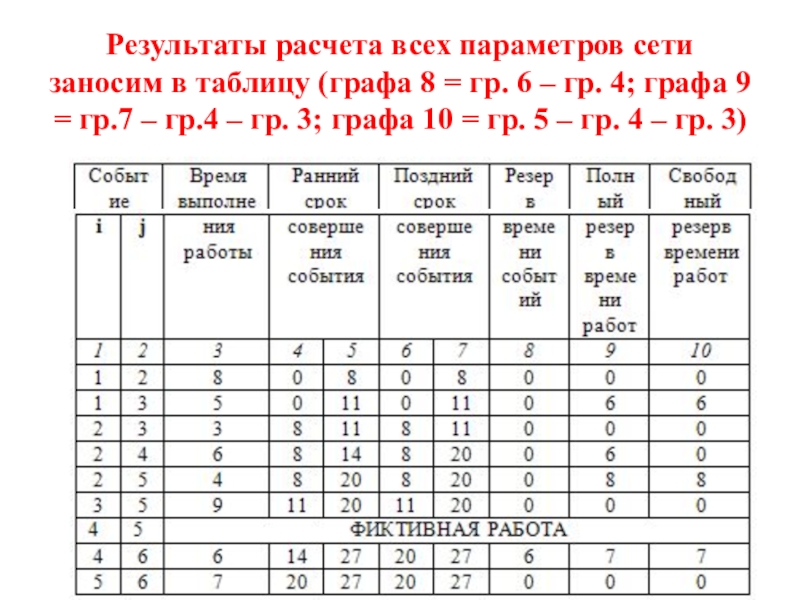
- 36. Результаты расчета всех параметров сети заносим в
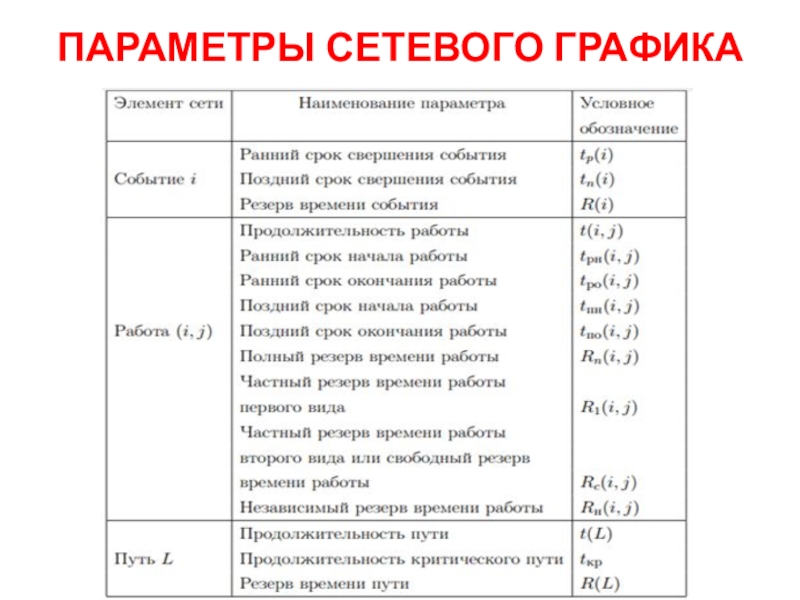
- 37. ПАРАМЕТРЫ СЕТЕВОГО ГРАФИКА
- 38. Скачать презентанцию
Теоретические сведения о сетевом планировании и управлении (1) Методы сетевого планирования и управления (СПУ), разработанные в начале 50-х годов, широко и успешно применяются для оптимизации планирования и управления сложными разветвленными комплексами работ,
Слайды и текст этой презентации
Слайд 1Лекция - семинар
Сетевое планирование и управление
Сетевое планирование и управление
Понятия сетевых
моделей. Сетевой график
построения сетевого графика и определение его параметровСлайд 2Теоретические сведения о сетевом планировании и управлении (1)
Методы сетевого планирования
и управления (СПУ), разработанные в начале 50-х годов, широко и
успешно применяются для оптимизации планирования и управления сложными разветвленными комплексами работ, требующими участия большого числа исполнителей и затрат ограниченных ресурсов. Для оптимизации сложных сетей, состоящих из нескольких сотен работ, вместо ручного счета следует применять типовые макеты прикладных программ по СПУ, имеющиеся в составе математического обеспечения ЭВМ.Слайд 3Теоретические сведения о сетевом планировании и управлении (2)
Система сетевого планирования
и управления (СПУ) - это системный подход к планированию сложных
динамических разработок с использованием графических, аналитических, организационных и контрольных мероприятий. СПУ позволяет моделировать и комплексно перестраивать план выполнения работ в условиях изменения внешних и внутренних факторов. Он позволяет определять оптимальные затраты времени и других ресурсов. СПУ реализуется в основном плановом документе — сетевой модели, которая представляет взаимосвязанные работы и события, развертывающиеся от начала до конца разработки.Слайд 4Этапы построения сетевого графика
Сетевое Планирование и Управление включает следующие этапы:
- определяется перечень событие и работ;
- строится сетевой график;
- рассчитываются параметры сетевого графика и определяется длительность критического пути;
- производится анализ сетевого графика и его оптимизация.
Слайд 5Понятия, используемые в сетевых моделях
Основными понятиями сетевых моделей являются понятия
события и работы.
Работа - это некоторый процесс, приводящий к
достижению определенного результата, требующий затрат каких-либо ресурсов и имеющий протяженность во времени. Событие - это момент времени, когда завершаются одни работы и начинаются другие.
Событие представляет собой результат проведенных работ и, в отличие от работ, не имеет протяженности во времени.
Слайд 6Понятие: работа
По своей физической природе работы можно рассматривать как:
1)
действие, 2) процесс, 3) ожидание
По количеству затрачиваемого времени работа
может быть: 1) действительной, 2) фиктивной
Слайд 7Сетевой график
Взаимосвязь работ и событий, необходимых для достижения конечной цели
проекта, изображается с помощью сетевого графика (сетевой модели). На сетевом
графике работы изображаются стрелками, которые соединяют вершины, изображающие события. Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями.Для идентификации конкретной работы используют код работы, состоящий из номеров начального и конечного событий
Слайд 9«Событие» в сетевом графике
Любое событие может считаться наступившим только тогда,
когда закончатся все входящие в него работы.
Поэтому, работы, выходящие
из некоторого события не могут начаться, пока не будут завершены все работы, входящие в это событие. Событие, не имеющее предшествующих ему событий, т.е. с которого начинается проект, называют исходным. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающим.Слайд 10Правила построения сетевого графика (1)
1. Длина стрелки не зависит от
времени выполнения работы.
2. Стрелка может не быть прямолинейным отрезком.
3. Для
действительных работ используются сплошные, а для фиктивных - пунктирные стрелки.4. Каждая операция должна быть представлена только одной стрелкой.
5. Между одними и теми же событиями не должно быть параллельных работ, т.е. работ с одинаковыми кодами.
6. Следует избегать пересечения стрелок;
Слайд 11Правила построения сетевого графика (2)
7. Не должно быть стрелок,
направленных справа налево.
8. Номер начального события должен быть меньше номера
конечного события.9. Не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме исходного.
10. Не должно быть тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего.
11. Не должно быть циклов.
Слайд 13Параметры сетевого графика (понятие пути)
Важное значение для анализа сетевых моделей
имеет понятие пути. Путь - это любая последовательность работ в
сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Различают следующие виды путей.Полный путь - это путь от исходного до завершающего события.
Критический путь - максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называют критическими. Подкритический путь - полный путь, ближайший по длительности к критическому пути
Слайд 14Параметры сетевого графика (временные характеристики)
На основании временных оценок рассчитываются
основные временные параметры сети: ранние и поздние сроки наступления всех
событий.Зная их, можно определить остальные параметры сети:
- ранние и поздние сроки начала и окончания работ,
- резервы времени событий,
- резервы времени работ.
Слайд 15Определение ранних сроков совершения событий -
- срок, необходимый для
выполнения всех работ, предшествующих данному событию. Он устанавливается путем выбора
максимального значения из продолжительности всех путей, ведущих от исходного к данному событию, то естьСлайд 16Определение поздних сроков совершения событий
- срок совершения события, который определяется
как разность между длительностью критического пути и продолжительностью максимального пути,
следующего за данным событием:Слайд 17Определение резерва времени совершения события
- резерв времени наступления события
i. Это такой промежуток времени, на который может быть отсрочено
наступление события i без нарушения сроков завершения проекта в целом. Начальные и конечные события критических работ имеют нулевые резервы событий.Слайд 18Представление показателей события на графике
Рассчитанные численные значения временных параметров записываются
прямо в вершины сетевого графика:
Слайд 19Определение полного резерва времени работы (1)
- полный резерв работы
показывает максимальное время, на которое может быть увеличена продолжительность работы
i, j или отсрочено ее начало, чтобы продолжительность проходящего через нее максимального пути не превысила продолжительности критического пути.Слайд 20Определение полного резерва времени работы (2)
Важнейшее свойство полного резерва
работы i, j заключается в том, что его частичное или
полное использование уменьшает полный резерв у работ, лежащих с работой i, j на одном пути. Таким образом, полный резерв принадлежит не одной данной работе i, j , а всем работам, лежащим на путях, проходящим через эту работу.Слайд 21Определение свободного резерва времени работы (1)
- свободный резерв работы
показывает максимальное время, на которое можно увеличить продолжительность работы i,
j или отсрочить ее начало, не меняя ранних сроков начала последующих работ.Слайд 22Определение свободного резерва времени работы (2)
Использование свободного резерва одной
из работ не меняет величины свободных резервов остальных работ сети.
Слайд 23Анализ сетевого графика с целью последующей его оптимизации
Анализ сетевого графика
осуществляется в два этапа:
Первый - проверка правильности построения сети
(правильность нумерации, выявление замкнутых контуров, «тупиковых» или «хвостовых» событий и т.д.) проводится визуально. Второй - определение напряженных зон работы с помощью коэффициентов напряженности.
Слайд 24КОЭФФИЦИЕНТ НАПРЯЖЁННОСТИ РАБОТ - Кн (i,j)
Кн (i,j) – это отношение
продолжительности несовпадающих, заключенных между одними и теми же событиями, отрезков
пути, одним из которых является отрезок проходящего через эти события критического пути, а другим - путь максимальной продолжительностиСлайд 26ОЦЕНКА КОЭФФИЦИЕНТА НАПРЯЖЁННОСТИ РАБОТ - Кн (i,j)
Чем выше коэффициент напряженности
Кн, тем сложнее выполнить работу в установленные критическим путем сроки.
После
анализа сетевого графика проводится его оптимизация, цель которой – сокращение длительности работ.Так как продолжительность критического пути определяет общую продолжительность работ по технической подготовке, то задача сокращения её сроков сводится к сокращению продолжительности работ, находящихся на критическом пути.
Слайд 27СОКРАЩЕНИЕ ПРОДОЛЖИТЕЛЬНОСТИ КРИТИЧЕСКОГО ПУТИ
Продолжительность критического пути может быть сокращена за
счёт расчленения дополнительными событиями на составляющие части и параллельное их
выполнение и за счёт перераспределения трудовых ресурсов с работ, имеющих резерв на родственную работу, лежащую на критическом пути, и др.После аналитических расчётов определяется новый критический путь и новый срок окончания всего комплекса работ.
Слайд 28КЛАССИФИКАЦИЯ КОЭФФИЦИЕНТОВ НАПРЯЖЁННОСТИ РАБОТ - Кн (i,j)
Вычисленные коэффициенты напряженности позволяют
дополнительно классифицировать работы по зонам. В зависимости от величины
Кн
(i,j) выделяют три зоны: критическую (Кн (i,j) > 0.8);
подкритическую (0.6 ≤ Кн (i,j) ≤ 0.8);
резервную (Кн (i,j) < 0.6).
Таким образом, можно распорядиться о перестановке ресурсов с работ резервной зоны на критические работы для уменьшения времени их выполнения.