Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекція 6. Графи
Содержание
- 1. Лекція 6. Графи
- 2. Слайд 2
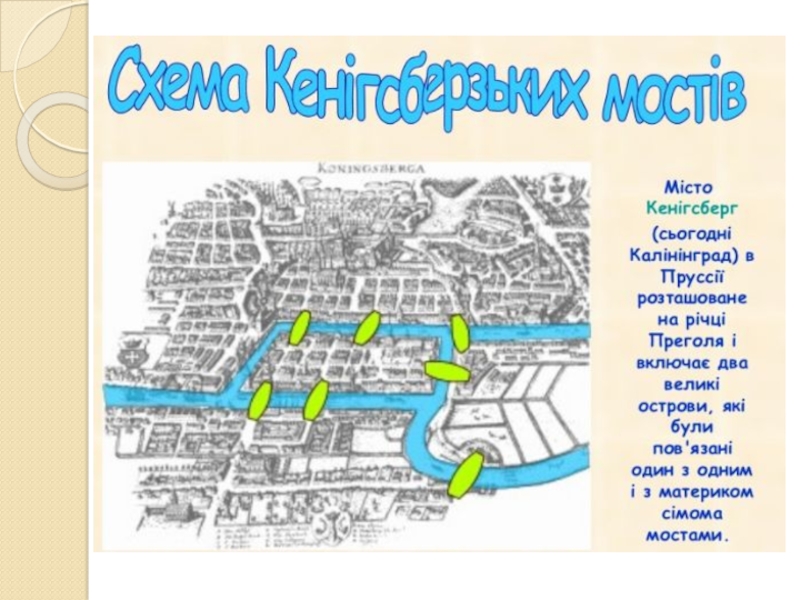
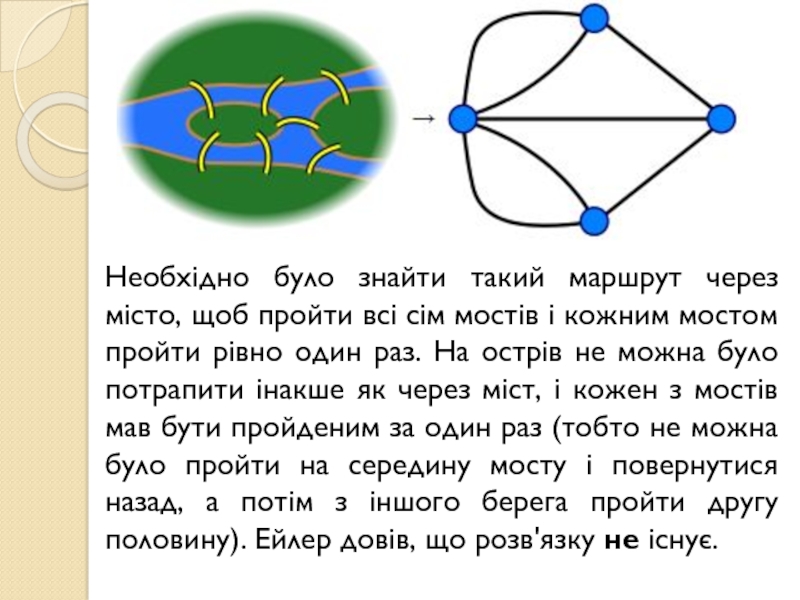
- 3. Необхідно було знайти такий маршрут через місто,
- 4. §1. Графи. Основні поняття і визначенняГраф G=(V,E)
- 5. За наочного подавання графа вершини зображуються точками,
- 6. Слайд 6
- 7. Звичайний граф з n вершинами, будь-яка пара
- 8. Теорема 1. Сума степенів усіх вершин графа
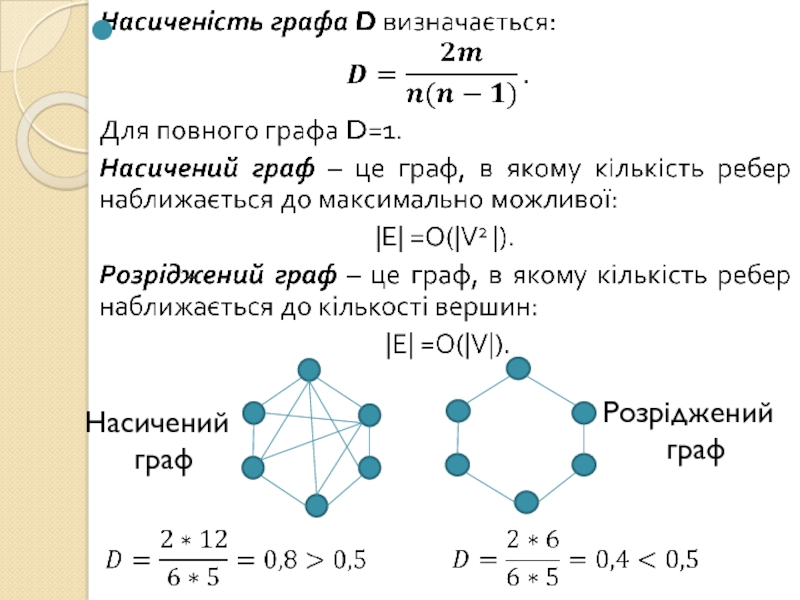
- 9. Насичений графРозріджений граф
- 10. Мультиграф – це граф із кратними ребрами.Псевдограф
- 11. Підграфом графа G=(X,V) називають граф G’=(X1,V1), для
- 12. Граф, вершини якого можна розбити на непересічні
- 13. Графи G1=(V1,E1) і G2=(V2,E2) називаються ізоморфними (позначення: G1~G2), якщо між графами існує взаємо-однозначне відображення j: G1
- 14. §2 Унарні операції над графами1. Доповнення.Доповненням графа
- 15. 2.Видалення вершини. Нехай xi – вершина графа
- 16. 4. Стягування.Стягування – операція видалення ребра l
- 17. §3 Бінарні операції над графами1. Об’єднання графів.Об’єднанням
- 18. 2. ПеретинПеретином графів G1 та G2, позначається
- 19. 3. Кільцева сума Кільцева сума двох графів
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4§1. Графи. Основні поняття і визначення
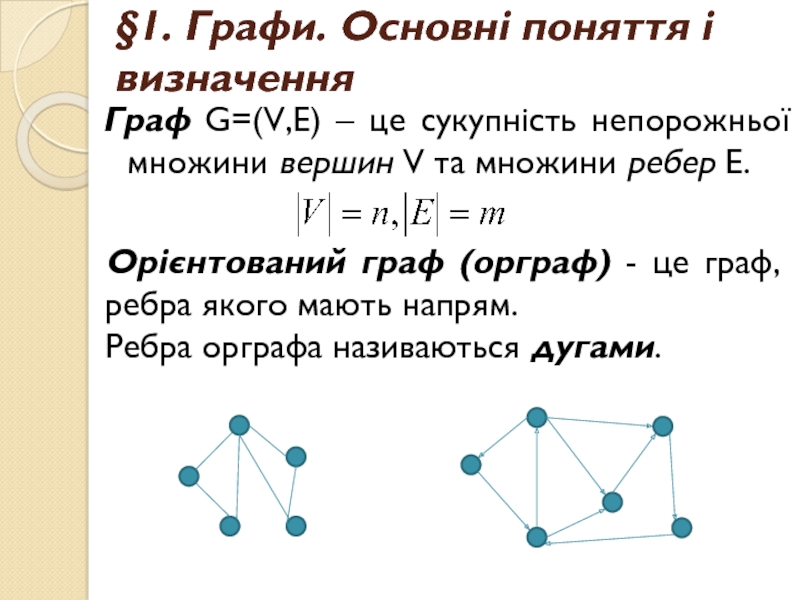
Граф G=(V,E) – це сукупність
непорожньої множини вершин V та множини ребер E.
Орієнтований граф
(орграф) - це граф, ребра якого мають напрям. Ребра орграфа називаються дугами.
Слайд 5За наочного подавання графа вершини зображуються точками, ребра – лініями,
які з’єднують точки.
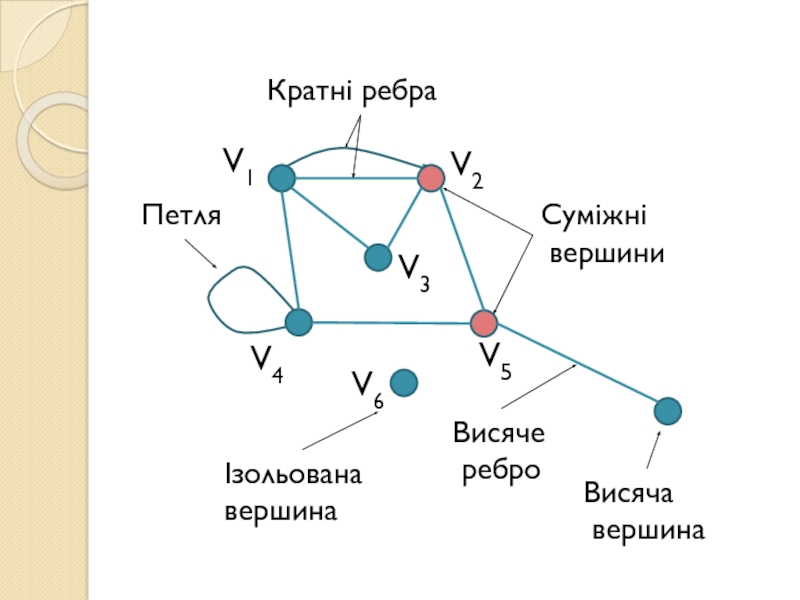
Кількість ребер, інцидентних до певної вершини x, називається
степенем цієї вершини і позначається d(x).Вершина, в якої степінь дорівнює 0, називається ізольованою. Вершини, які мають степінь 1, називаються висячими, або кінцевими .
Петлями називають ребра, які мають збіжні кінці.
Граф, який не має ребер (U = ∅), називається порожнім. Усі вершинипорожнього графа є ізольовані.
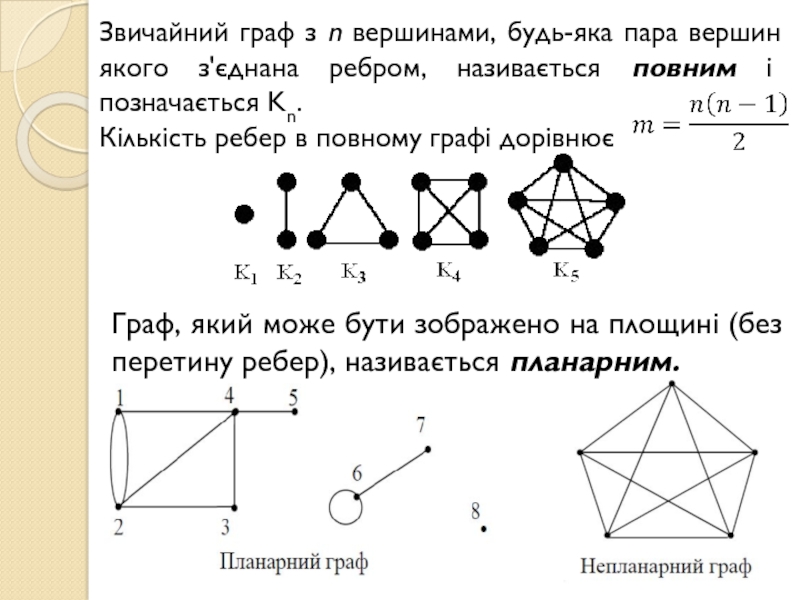
Слайд 7Звичайний граф з n вершинами, будь-яка пара вершин якого з'єднана
ребром, називається повним і позначається Kn.
Кількість ребер в повному графі
дорівнюєГраф, який може бути зображено на площині (без перетину ребер), називається планарним.
Слайд 8Теорема 1. Сума степенів усіх вершин графа дорівнює подвоєній кількості
ребер.
Д о в е д е н н я
Кожне ребро
двічі входить до суми, звідки й випливає твердження.Теорема 2. У кожному графі число вершин, які мають непарний степінь, є парне.
Д о в е д е н н я
Нехай X1 ⊆ X – множина вершин непарного степеня; X2 ⊆ X – множина вершин парного степеня. Зазначимо, що X = X1 ∪ X2; X1 ∩ X2 = ∅.
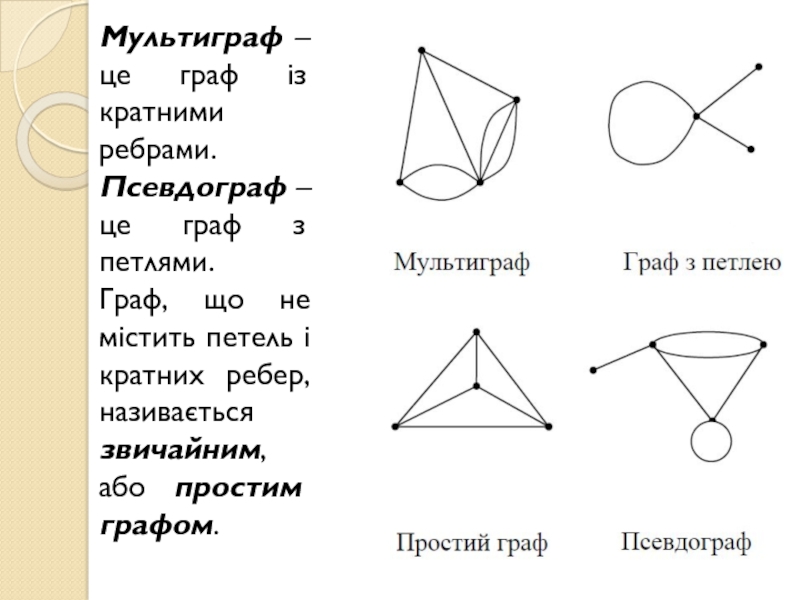
Слайд 10Мультиграф – це граф із кратними ребрами.
Псевдограф – це граф
з петлями.
Граф, що не містить петель і кратних ребер,
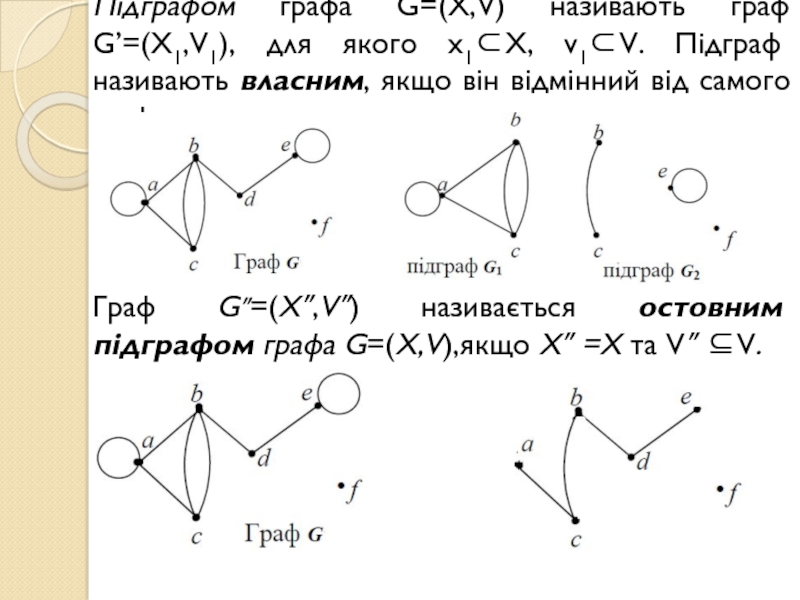
називається звичайним, або простим графом.Слайд 11Підграфом графа G=(X,V) називають граф G’=(X1,V1), для якого х1X, v1V.
Підграф називають власним, якщо він відмінний від самого графа.
Граф
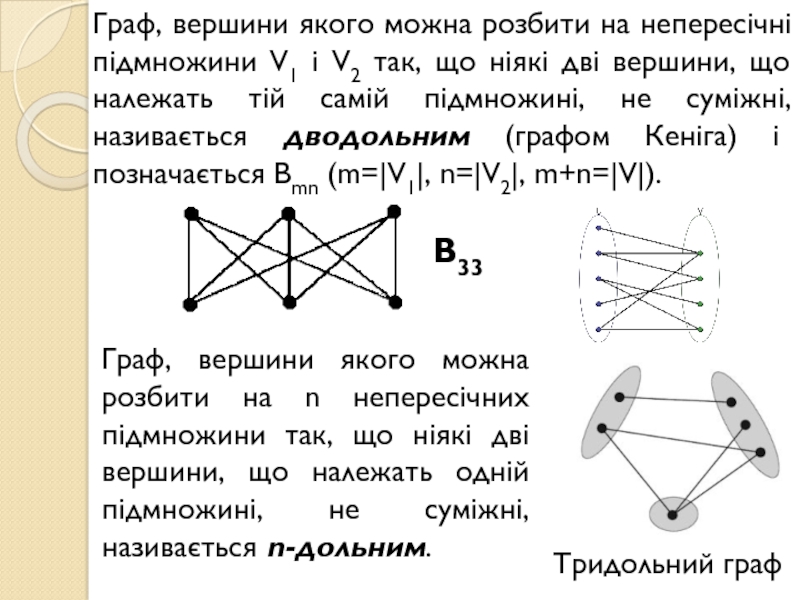
G=(X,V) називається остовним підграфом графа G=(X,V),якщо X =X та V ⊆V.Слайд 12Граф, вершини якого можна розбити на непересічні підмножини V1 і
V2 так, що ніякі дві вершини, що належать тій самій
підмножині, не суміжні, називається дводольним (графом Кеніга) і позначається Bmn (m=|V1|, n=|V2|, m+n=|V|).B33
Граф, вершини якого можна розбити на n непересічних підмножини так, що ніякі дві вершини, що належать одній підмножині, не суміжні, називається n-дольним.
Тридольний граф
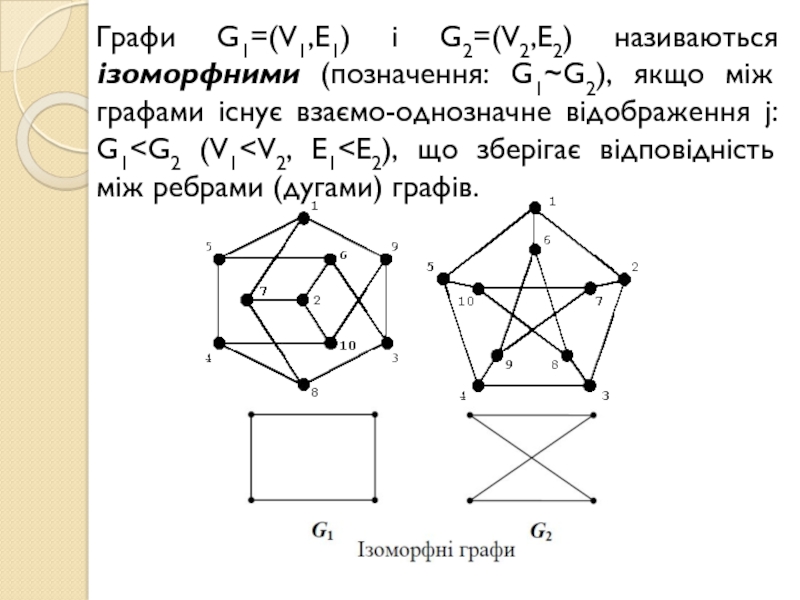
Слайд 13Графи G1=(V1,E1) і G2=(V2,E2) називаються ізоморфними (позначення: G1~G2), якщо між
графами існує взаємо-однозначне відображення j: G1
відповідність між ребрами (дугами) графів.Слайд 14§2 Унарні операції над графами
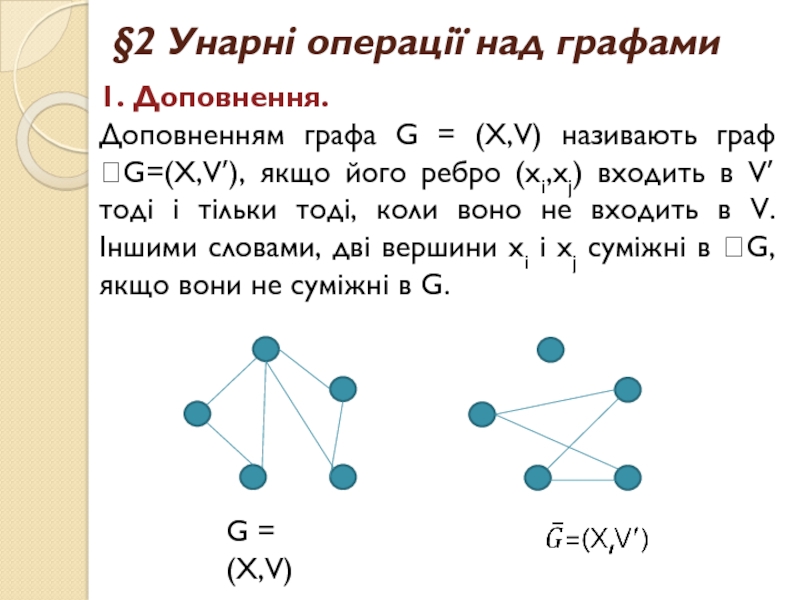
1. Доповнення.
Доповненням графа G = (X,V)
називають граф G=(X,V), якщо його ребро (xi,xj) входить в V
тоді і тільки тоді, коли воно не входить в V. Іншими словами, дві вершини xi і xj суміжні в G, якщо вони не суміжні в G.G = (X,V)
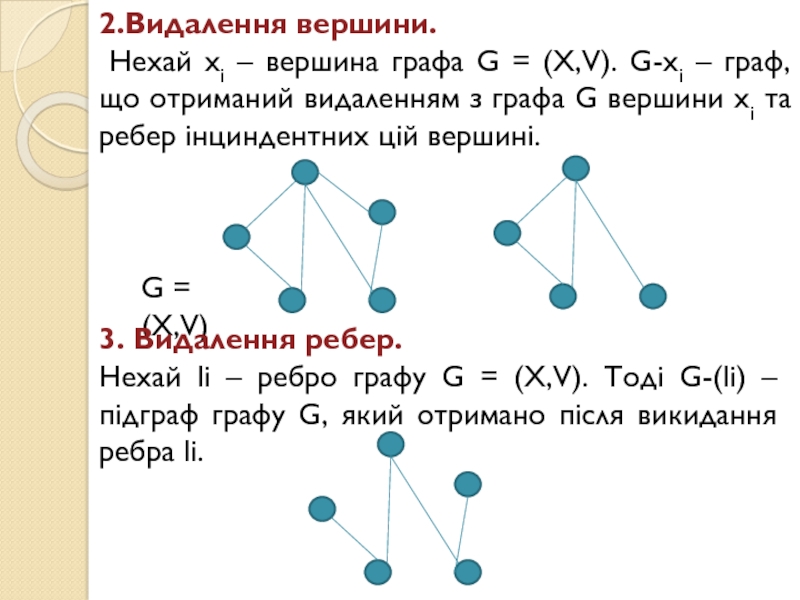
Слайд 152.Видалення вершини.
Нехай xi – вершина графа G = (X,V).
G-xi – граф, що отриманий видаленням з графа G вершини
xі та ребер інциндентних цій вершині.G = (X,V)
3. Видалення ребер.
Нехай li – ребро графу G = (X,V). Тоді G-(li) – підграф графу G, який отримано після викидання ребра li.
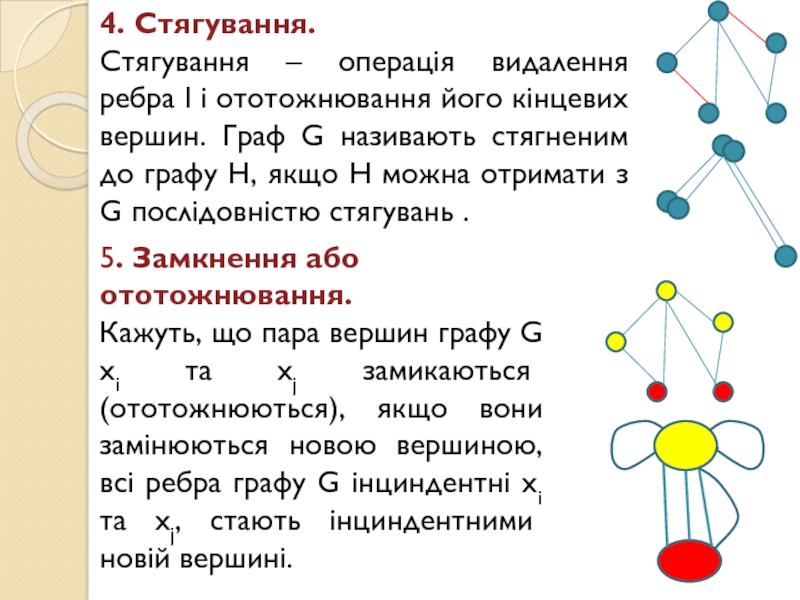
Слайд 164. Стягування.
Стягування – операція видалення ребра l і ототожнювання його
кінцевих вершин. Граф G називають стягненим до графу Н, якщо
Н можна отримати з G послідовністю стягувань .5. Замкнення або ототожнювання.
Кажуть, що пара вершин графу G xi та xj замикаються (ототожнюються), якщо вони замінюються новою вершиною, всі ребра графу G інциндентні xi та xj, стають інциндентними новій вершині.
Слайд 17§3 Бінарні операції над графами
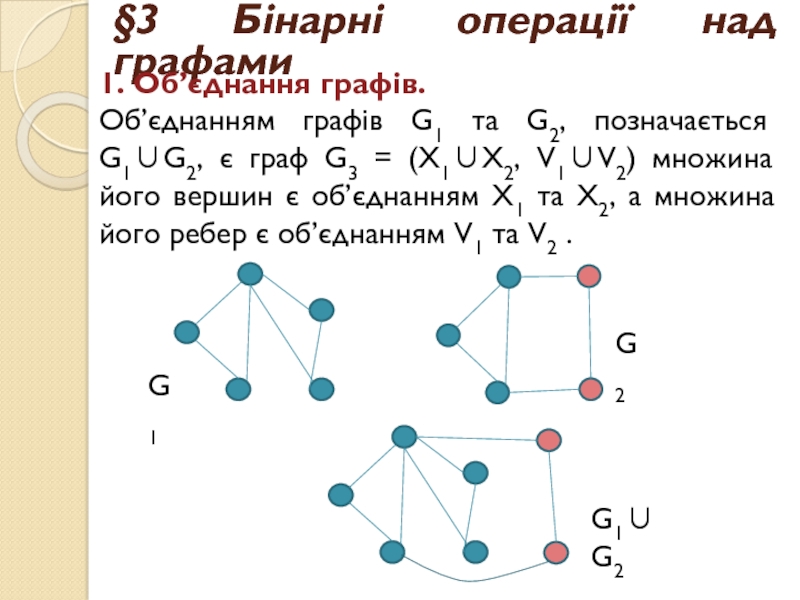
1. Об’єднання графів.
Об’єднанням графів G1 та
G2, позначається G1G2, є граф G3 = (X1X2, V1V2) множина
його вершин є об’єднанням X1 та X2, а множина його ребер є об’єднанням V1 та V2 .G1
G1G2
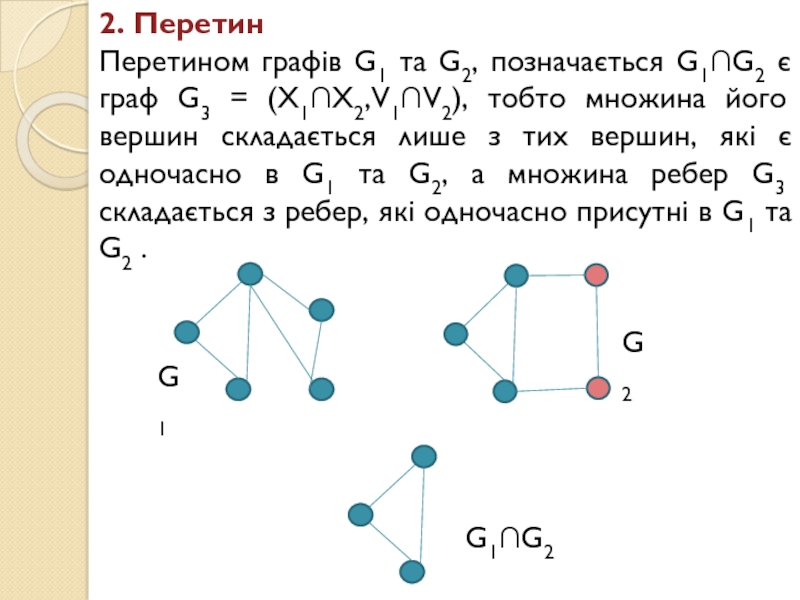
Слайд 182. Перетин
Перетином графів G1 та G2, позначається G1G2 є граф
G3 = (X1X2,V1V2), тобто множина його вершин складається лише з
тих вершин, які є одночасно в G1 та G2, а множина ребер G3 складається з ребер, які одночасно присутні в G1 та G2 .G1
G1G2
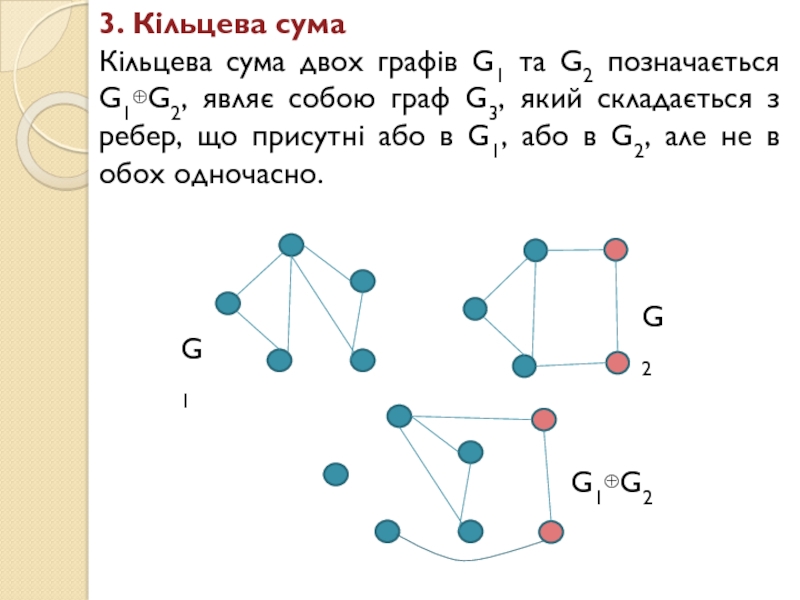
Слайд 193. Кільцева сума
Кільцева сума двох графів G1 та G2
позначається G1G2, являє собою граф G3, який складається з ребер,
що присутні або в G1, або в G2, але не в обох одночасно.G1
G1G2