Лекція № 2 ( 3 ) Б агатошарові композити

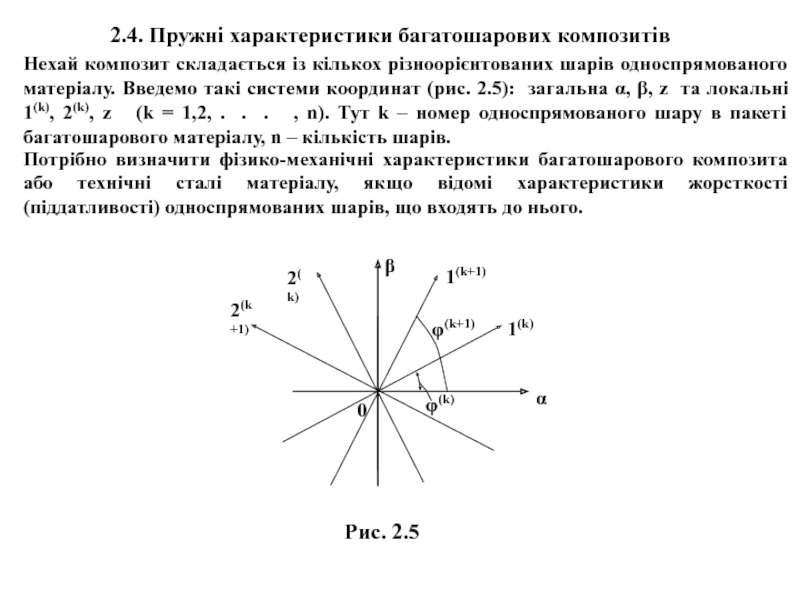
шарів односпрямованого матеріалу. Введемо такі системи координат (рис. 2.5): загальна

Потрібно визначити фізико-механічні характеристики багатошарового композита або технічні сталі матеріалу, якщо відомі характеристики жорсткості (піддатливості) односпрямованих шарів, що входять до нього.

Рис. 2.5

одиничної довжини та ширини (рис. 2.6).
Рис. 2.6
Внутрішні зусилля

де

(2.68)

n – кількість шарів у пакеті;

нормальне напруження в k-шарі у напрямі осі α; нормальне напруження в k-шарі у напрямі осі β; дотичне напруження в k-шарі у площині α0β .

Якщо розділити праві й ліві частини рівняння (2.68) на сумарну товщину пакета

отримаємо

(2.69)

де

середні по товщині пакета напруження, які дорівнюють

відносна товщина k-шару.

(2.58) у вигляді
і враховуючи те, що

де

(2.70)

(2.72)

або

(2.72*)

(2.71)

(2.73)

Для визначення технічних сталих пружності багатошарового композита можна розглянути деформацію розтягання такого композита у напрямі осі α. Рівняння (2.72*) при цьому набере вигляду

(2.74)

Записавши і із двох останніх рівнянь (2.74) як функції і підставивши
їх у перше рівняння системи (2.74), отримаємо

матриці

визначник матриці

Аналогічним шляхом знаходять інші значення технічних сталих

(2.76)

(2.78)

а також коефіцієнти Пуассона

(2.77)

У випадку ортотропного композита, якщо отримаємо вже відомі
формули типу (2.42):

(2.79)

Із рівнянь (2.72) – (2.73) безпосередньо дістанемо висновок, що порядок чергування шарів у пакеті багатошарового матеріалу не має значення при підрахунку його жорсткості .