Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная засечка
Содержание
- 1. Линейная засечка
- 2. Отсюда
- 3. Координаты точки Р:
- 4. Среднюю квадратическую ошибку в положении пункта Р,
- 5. Рассмотренная обратная засечка по трем исходным пунктам
- 6. Задача решается дважды при различном сочетании исходных
- 7. Отсюда допустимое расхождение в значениях вычисленных координат
- 8. 4. Линейная засечка. Задача линейной засечки заключает-ся
- 9. Даны координаты пунктов А, B, C. Измерены
- 10. Рассмотрим однократную засечку с использованием пунктов А
- 11. 2. Определим угол β1, используя теорему косинусов: 3. Определим дирекционный угол линии АР
- 12. 4. Определим координаты точки Р: Для контроля
- 13. Расхождение не должно превышать 3-х единиц последнего
- 14. Допускается|СР–S3|
- 15. Допустимое расхождение в координатах определяют по формуле В свою очередь
- 16. где М1 и М2 – СКО положения
- 17. Величину угла засечки (для первого решения) можно
- 18. Тема: «ЭЛЕКТРОННЫЕ ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ РАССТОЯНИЙ»
- 19. 1. Принцип и методы измерения расстояний. 2.
- 20. 6. Общие сведения о светодальномерах.7. Светодальномер СТ5.8.
- 21. Литература Помелов С.И. Электронные дальномеры: Лекция. –
- 22. 1.Принципы и методы измерения расстояний. Физический принцип
- 23. Идея определения расстояний электромаг-нитными дальномерами довольно проста.
- 24. Электромагнитные волны, посланные из точки А, отражаются
- 25. В настоящее время скорость распространения
- 26. Задача сводится к определению времени
- 27. Импульсный метод характеризуется сравнительно большой абсолютной погрешностью.
- 28. Частотный метод основан на использовании частотно-модулированных колебаний
- 29. Интерференционный метод основан на непосредственном наблюдении результата
- 30. Фазовый метод. Этот метод измерения расстояний наиболее
- 31. 2. Фазовый методВ большинстве устройств для измерения
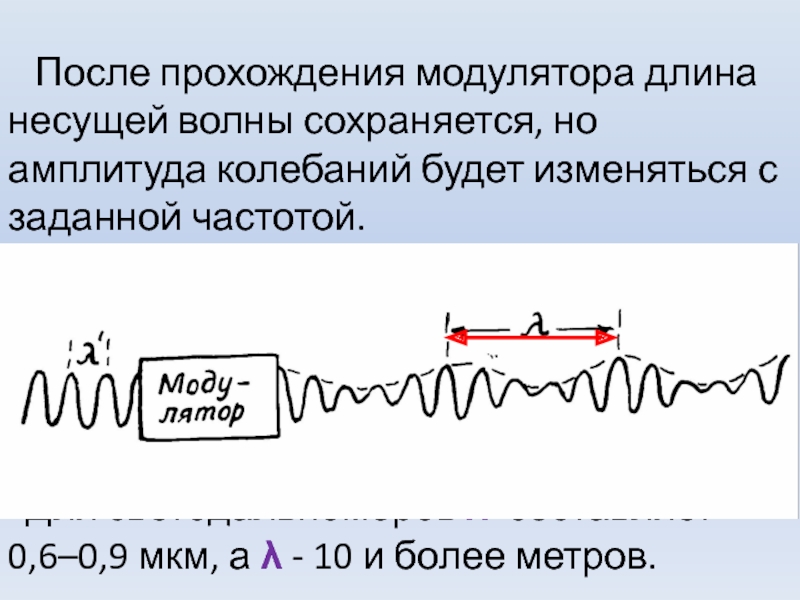
- 32. Амплитудная модуляция показана на рис. До
- 33. После прохождения модулятора длина несущей
- 34. Пусть передатчик излучает электромаг-нитные колебания с частотой
- 35. Пусть для какого-то момента времени t колебания,
- 36. Разность фаз составитОтсюдагде N – целое число
- 37. В результате получим формулуВ этой формуле величину
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Отсюда
Вычислив значения А и В, определим углы φ и ψ
φ = А+ В,
ψ = А – В.
Далее определим длину линии АР
Слайд 3 Координаты точки Р:
Для контроля координат точки Р можно вычислить второй раз, используя формулы
Слайд 4Среднюю квадратическую ошибку в положении пункта Р, определенного обратной засечкой,
можно вычислить по формуле
где mβ – СКО измерения углов
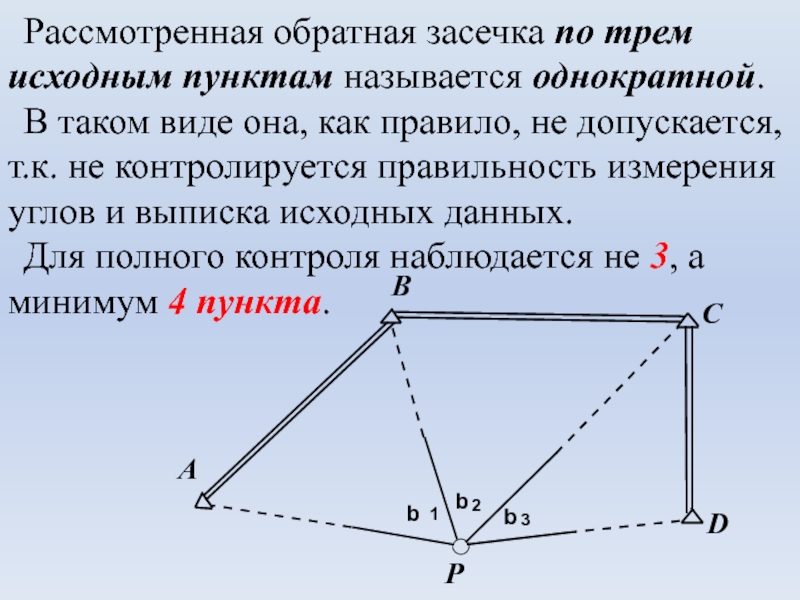
β1 и β2.Слайд 5Рассмотренная обратная засечка по трем исходным пунктам называется однократной.
В
таком виде она, как правило, не допускается, т.к. не контролируется
правильность измерения углов и выписка исходных данных.Для полного контроля наблюдается не 3, а минимум 4 пункта.
Слайд 6Задача решается дважды при различном сочетании исходных пунктов. Например, первый
раз используются пункты А, В, С и второй раз пункты
В, С, D. Для каждого варианта решения определяется СКО положения пункта М .Ожидаемое среднее квадратическое значение Mr расхождения в положении пункта Р при двух решениях составит
Слайд 7Отсюда допустимое расхождение в значениях вычисленных координат можно установить по
формуле
где X/ , Y/ – координаты точки из 1-го
решения;X// , Y// – координаты точки из 2-го решения.
За окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку
Слайд 84. Линейная засечка.
Задача линейной засечки заключает-ся в определении координат
третьего пункта по координатам двух исходных пунктов и измеренным расстояниям
от определяемого пункта до исходных (однократная засечка).Для контроля определения используют-ся координаты третьего исходного пункта и расстояния до него от опреде-ляемого.
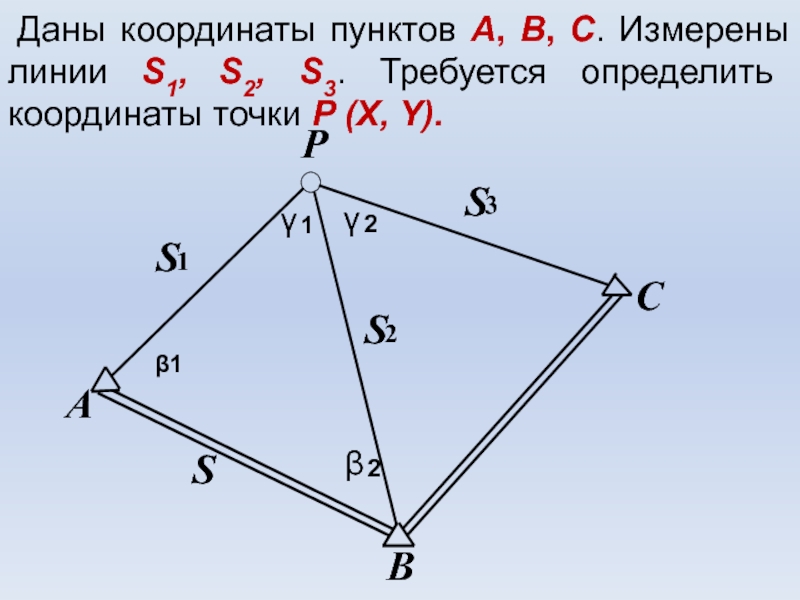
Слайд 9Даны координаты пунктов А, B, C. Измерены линии S1, S2,
S3. Требуется определить координаты точки P (X, Y).
Слайд 10Рассмотрим однократную засечку с использованием пунктов А и В.
1. Решением
обратной геодезической задачи определим дирекционный угол и длину линии АВ:
Слайд 124. Определим координаты точки Р:
Для контроля решения задачи вычисляется
длина линии ВР и сравнивается с измеренной
Слайд 13Расхождение не должно превышать 3-х единиц последнего знака в измеренном
значении линии S2.
Для полного контроля определения вычисляется сторона СР и
сравнивается с измеренной S3
Слайд 14 Допускается
|СР–S3|
Однако в целях повышения точности окончательных
значений искомых координат задачу лучше решать дважды. При втором решении используют исходные пункты В, С и расстояния S2, S3. Слайд 16
где М1 и М2 – СКО положения пункта Р, определенного
линейной засечкой в первом и втором вариантах;
γ – угол засечки. Слайд 17Величину угла засечки (для первого решения) можно найти из выражения
За окончательное значение координат пункта Р берут среднее арифметическое,
которое будет иметь ошибку
Слайд 191. Принцип и методы измерения расстояний.
2. Сущность фазового метода.
3. Импульсно-фазовый метод.
4.Способы разрешения неоднозначности.
5. Точность измерения расстояний электронными дальномерами.
Слайд 206. Общие сведения о светодальномерах.
7. Светодальномер СТ5.
8. Поверки светодальномера СТ5
и измерение расстояний.
9. Безотражательная технология измерения расстояний.
10. Лазерные рулетки.
Слайд 21Литература
Помелов С.И. Электронные дальномеры: Лекция. – Горки: БГСХА, 2004.
– 28 с.
Помелов С.И. Электронные тахеометры: Лекция. – Горки:
БГСХА, 2004. – 36 с. А.В.Маслов,А.В.Гордеев,Ю.Г.Батраков. Геодезия. – М.: КолосС, 2006. – 598 с.
Геодезия:Учебно-методический комплекс/ БГСХА; Сост. С. И. Помелов, Д. А. Чиж. – Горки, 2006. 256 с.
Слайд 221.Принципы и методы измерения расстояний.
Физический принцип действия электронных (электромагнитных)
дальномеров основан на определении времени прохождения измеряемого расстояния электромагнитными волнами.
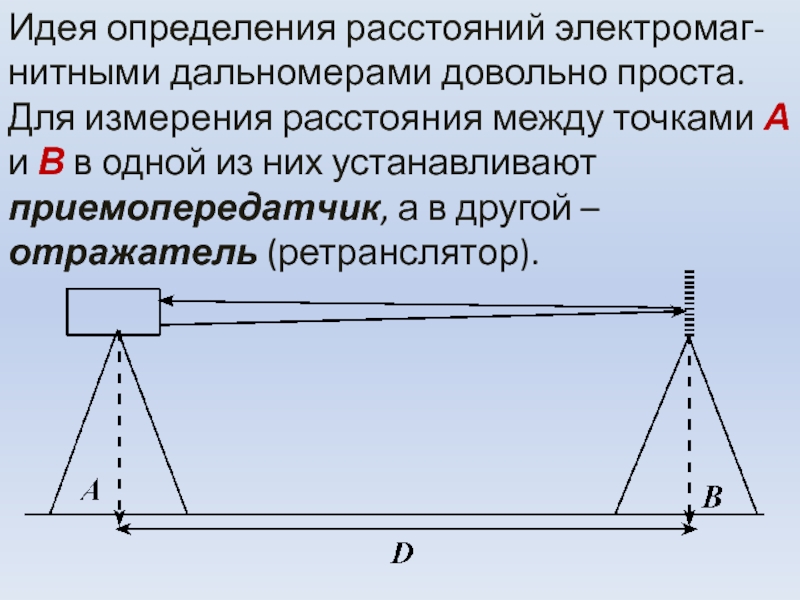
Слайд 23Идея определения расстояний электромаг-нитными дальномерами довольно проста. Для измерения расстояния
между точками А и В в одной из них устанавливают
приемопередатчик, а в другой – отражатель (ретранслятор).Слайд 24Электромагнитные волны, посланные из точки А, отражаются в точке В
и возвращаются обратно. Если определить время прохождения волн вперед и
обратно, то искомое расстояние можно вычислить по формулегде v – скорость распространения волн;
τ – время;
D – искомое расстояние.
Слайд 25 В настоящее время скорость распространения электромагнитных волн в
вакууме известна с высокой точностью и принята равной: с =
299792458 м/с ± 1,2 м/с.Действительную скорость распространения электромагнитных волн при измерении расстояний определяют по формуле
где n – показатель преломления воздуха, завися-щий от температуры, давления и влажности (n ≈ 1,000296).
Слайд 26 Задача сводится к определению времени τ.
В зависимости
от способов ее решения различают следующие методы измерения расстояний.Временной (импульсный) метод.
Это метод прямого измерения времени распространения электромагнитных волн. Импульсный дальномер содержит измеритель временных интервалов, запускаемый опорным импульсом от передатчика и, останавливаемый импульсом, пришедшим с дистанции.
Слайд 27Импульсный метод характеризуется сравнительно большой абсолютной погрешностью. Поэтому его целесообразно
использовать для измерения больших расстояний, когда относительная ошибка измерения получается
малой.Слайд 28Частотный метод основан на использовании частотно-модулированных колебаний и сводится к
измерению приращения частоты за время распространения этих колебаний до объекта
и обратно. Точность таких приборов порядка 1:1000.Применяется он, в основном, в самолетных радиовысотомерах и радиолокационных системах.
Слайд 29Интерференционный метод основан на непосредственном наблюдении результата интерференции двух (или
более) когерентных световых волн, прошедших различные расстояния.
Применяется для измерения
небольших расстояний с высокой точностью. Слайд 30Фазовый метод. Этот метод измерения расстояний наиболее распространен в геодезии.
Применяется для измерения расстояний от нескольких метров до десятков (а
в радиодиапазоне – до сотен) км.Слайд 312. Фазовый метод
В большинстве устройств для измерения расстояний используются модулированные
электромагнитные колебания.
Модуляция – это изменение какого-либо параметра (амплитуды, частоты
или фазы) по какому-либо закону. В качестве модулятора в настоящее время широко применяют полупроводниковые лазеры на основе кристалла арсенида галлия с длиной волны излучения 0,9 мкм.
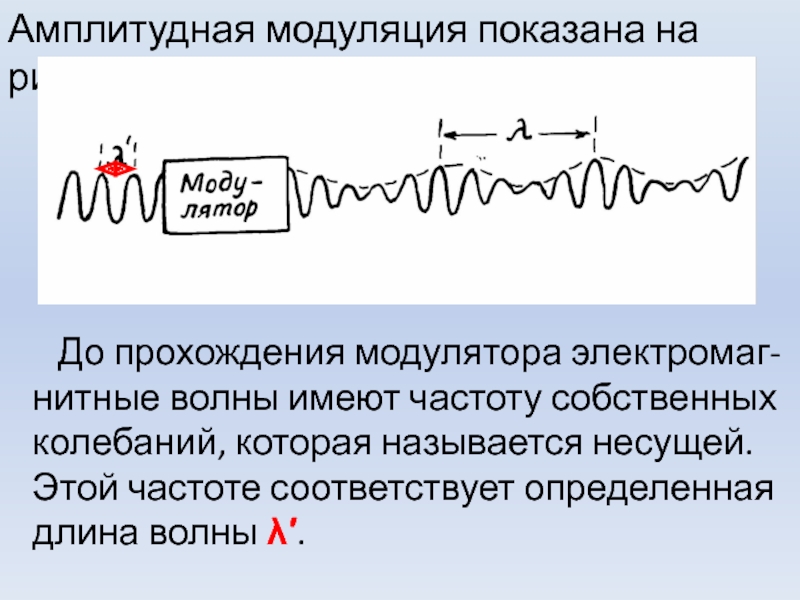
Слайд 32Амплитудная модуляция показана на рис.
До прохождения модулятора
электромаг-нитные волны имеют частоту собственных колебаний, которая называется несущей. Этой
частоте соответствует определенная длина волны λ′.Слайд 33 После прохождения модулятора длина несущей волны сохраняется, но
амплитуда колебаний будет изменяться с заданной частотой.
Частота модулирования
колебаний называется измерительной. Ей соответст-вует измерительная длина волны λ, которая и выполняет роль «мерной ленты». Для светодальномеров λ′ составляет 0,6–0,9 мкм, а λ - 10 и более метров.
Слайд 34Пусть передатчик излучает электромаг-нитные колебания с частотой f , которой
соответствует длина волны
Эти колебания направляются на отражатель, а также минуя
дистанцию в приемную часть. Приемник усиливает их и направляет на индикатор сдвига фаз.Слайд 35Пусть для какого-то момента времени t колебания, пришедшие с дистанции,
имеют фазу
где 2πf– круговая частота.
Колебания, поступающие в приемник, минуя дистанцию,
для этого же момента будут иметь фазу
Слайд 36Разность фаз составит
Отсюда
где N – целое число волн, уложившихся в
расстоянии 2D;
ΔN – домер фазового цикла или некоторая для периода,
измеряемая фазометром.Слайд 37В результате получим формулу
В этой формуле величину λ можно вычислить
по известной частоте, ΔN – измерить фазометром, N – остается
неизвестным.Определение целого числа периодов N называют разрешением неоднозначности.