Слайд 2Основные идеи линейного программирования возникли во время второй мировой войны
в
связи с поиском оптимальных стратегий при ведении военных операций. С
тех пор они
нашли широкое применение в промышленности, торговле и управлении - как в местных, так и в государственных масштабах. Этими методами можно решить многие (хотя не все) задачи, связанные с эффективным использованием ограниченных ресурсов.
Слайд 3Линейное программирование - это раздел прикладной математики о методах исследования
и отыскания наибольших или наименьших значений линейной функции, на неизвестные
которой наложены линейные ограничения.
Слайд 4Термин «линейное программирование» появился в 1951 году в работах американских
ученых Дж. Б. Данцига, Тьяллинга Купманса (Koopmans). Слово «программирование» объясняется
тем, что набор искомых переменных определяет программу (план) работы некоторого экономического объекта.
Слайд 5Круг задач, решаемых при помощи методов линейного программирования достаточно широк.
Это, например:
задача об оптимальном использовании ресурсов при производственном планировании;
задача о смесях (планирование состава продукции);
задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");
транспортные задачи (анализ размещения предприятия, перемещение грузов).
Слайд 6В общем виде задача линейного программирования может быть сформулирована следующим
образом.
Дана линейная функция
Ф = с1·х1 + с2·х2 + . .
. +cj·xj+ . . . + сn·хn (1)
Слайд 7система линейных ограничений
a11· x1 + a12·x2 + . . .
+ a1j·xj + . . . + a1n·xn = b1,
a21·
x1 + a22·x2 + . . . + a2j·xj + . . . + a2n·xn = b2,
. . . . . . . . (2)
a i1 · x1+ a i2·x2 + . . . + aij·xj + . . . + a in·xn = bi,
. . . . . . . .
am1· x1 + am2·x2 + . . .+ amj·xj + . . .+ amn ·xn = bm,
и условия неотрицательности переменных
xj ≥ 0, j = 1, n (3)
где aij, bi и cj - заданные постоянные величины.
Слайд 8Задача об оптимальном использовании ресурсов при производственном планировании
Общий смысл задач
этого класса сводится к следующему.
Предприятие выпускает n различных изделий.
Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b1, b2,..., bm условных единиц.
Известны также технологические коэффициенты aij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида ( ).
Слайд 9Прибыль, получаемая предприятием при реализации изделия j-го вида, равна cj.
В
планируемом периоде значения величин aij, biи cj остаются постоянными.
Требуется составить
такой план выпуска продукции, при реализации которого прибыль предприятия была бы наибольшей.
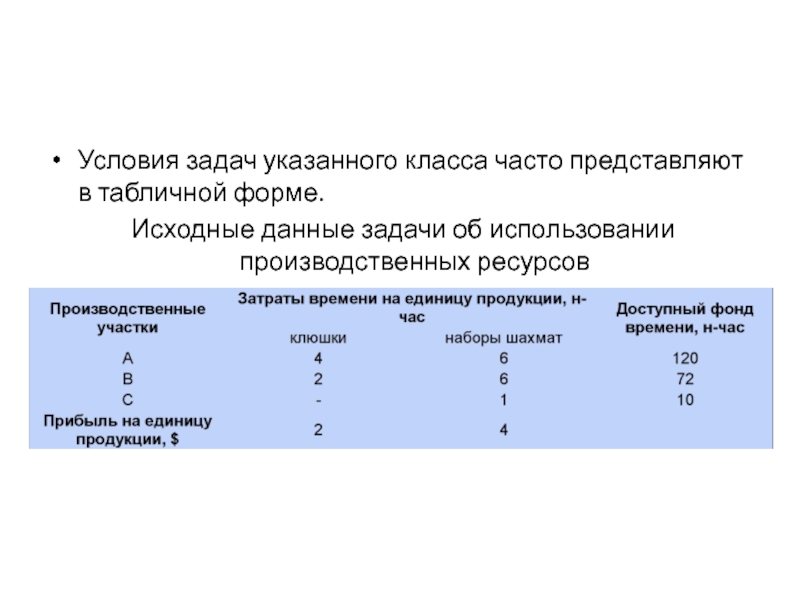
Слайд 10пример задачи этого класса
Компания специализируется на выпуске хоккейных клюшек и
наборов шахмат. Каждая клюшка приносит компании прибыль в размере $2,
а каждый шахматный набор - в размере $4. На изготовление одной клюшки требуется четыре часа работы на участке A и два часа работы на участке B. Шахматный набор изготавливается с затратами шести часов на участке A, шести часов на участке B и одного часа на участке C. Доступная производственная мощность участка A составляет 120 н-часов в день, участка В - 72 н-часа и участка С - 10 н-часов.
Сколько клюшек и шахматных наборов должна выпускать компания ежедневно, чтобы получать максимальную прибыль?
Слайд 11Условия задач указанного класса часто представляют в табличной форме.
Исходные данные задачи об использовании производственных ресурсов
Слайд 12По данному условию сформулируем задачу линейного программирования.
Обозначим: x1- количество
выпускаемых ежедневно хоккейных клюшек, x2- количество выпускаемых ежедневно шахматных наборов.
Формулировка
ЗЛП:
= 2x1+ 4x2→ max;
4x1+ 6x2≤ 120,
2x1+ 6x2≤ 72,
x2≤ 10;
x1≥ 0, x2≥ 0.
Слайд 13 Каждое неравенство в системе функциональных ограничений соответствует в
данном случае тому или иному производственному участку, а именно: первое
- участку А, второе - участку В, третье - участку С.
Слайд 14Задача о смесях (планирование состава продукции).
На птицеферме употребляются два вида
кормов - I и II. В единице массы корма I
содержатся единица вещества A, единица вещества В и единица вещества С. В единице массы корма II содержатся четыре единицы вещества А, две единицы вещества В и не содержится вещество C. В дневной рацион каждой птицы надо включить не менее единицы вещества А, не менее четырех единиц вещества В и не менее единицы вещества С. Цена единицы массы корма I составляет 3 рубля, корма II - 2 рубля.
Составьте ежедневный рацион кормления птицы так, чтобы обеспечить наиболее дешевый рацион.