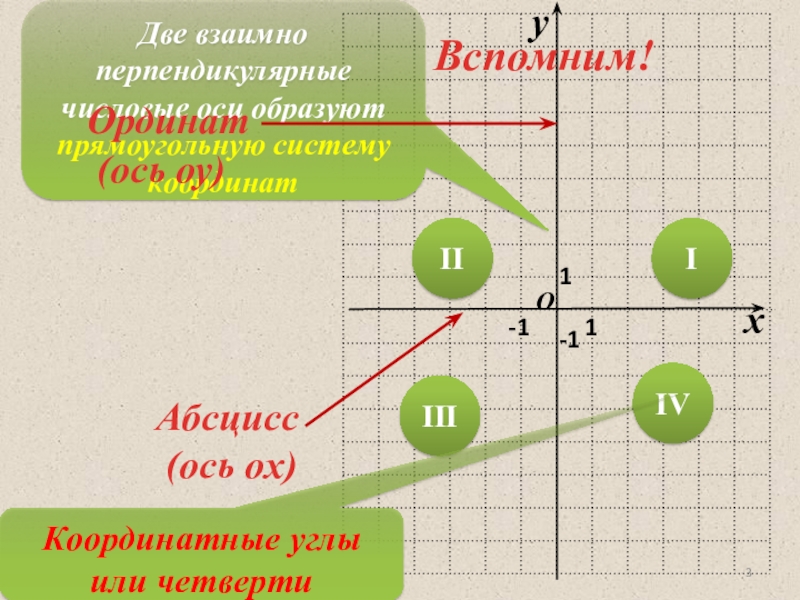
координатной плоскости.
Разберемся с понятием об уравнении с двумя переменными, их
решением и графиком уравнения.Научимся строить график линейного уравнения с двумя переменными.
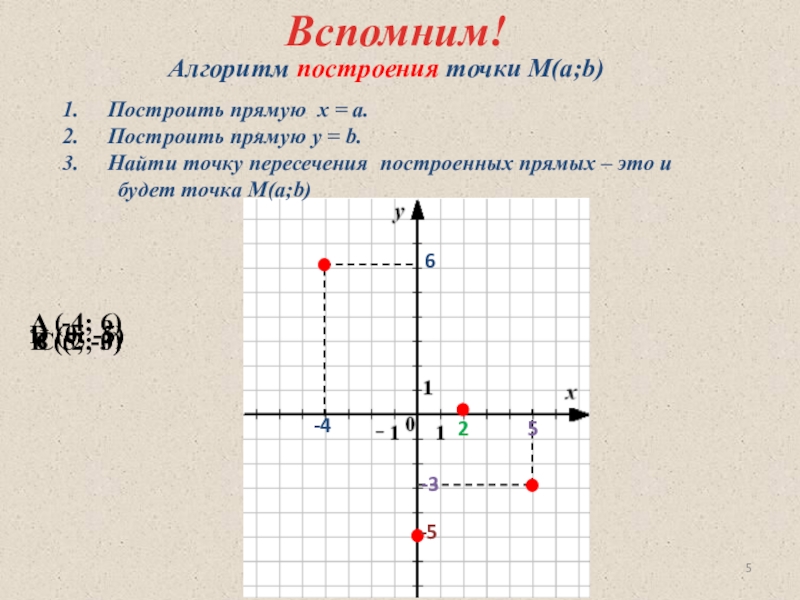
Запомним алгоритм построения графика линейного уравнения с двумя переменными.