Слайд 1Масиви
Масиви належать до складених типів даних. Масив являє собою кінцеву
іменовану послідовність величин одного типу (елементів масиву). Опис масивів у
програмі відрізняється від опису простої змінної наявністю після імені квадратних дужок «[ ]», в яких задається кількість елементів масиву (розмірність). Нумерація елементів масиву починається з 0.
Одновимірні масиви - це лінійна послідовність однотипних елементів (вектор). Кожен елемент має свій порядковий номер (індекс).
Масиви повинні бути оголошені явно, щоб компілятор міг виділити неперервну ділянку пам’яті обсягом
n * sizeof ( тип елементів)
[
] = {значення};
Приклад:
float m [6];
float m [6] = {3.4, 4.5, 5.6, 6.7, 8.9, 10.3};
float m [ ] = {3.45, 4.56, 5.67, 6.78};
Надалі кількість елементів змінити неможливо. Для того, щоб обнулити елементи оголошеного масиву, достатньо ініціювати його перший елемент:
int mas [0]= {0};
Слайд 3За замовчуванням, якщо в оголошеному масиві ініціюється тільки декілька перших
елементів, то його інші елементи ініціюються нулями. Так, у випадку,
коли
float mas [10] = {2.2, 34.56},
останні вісім елементів масиву одержать значення 0.
Доступ до елементів реалізується через індекси або через вказівники (адреси).
У разі доступу через індекси застосовують конструкцію
ім’я масиву [індекс елементу]
Індекс може бути довільним виразом цілого типу: arr [ 2*k-5 ]
Слайд 5Приклад: Обчислити середнє арифметичне від’ємних
елементів масиву х[10] та
їх кількість.
#include < stdio.h >
void main();
{ int mas [10], i, k, s;
float sa;
k=0; s=0;
puts (“ Введіть елементи масиву\n”);
for ( i=0; i<10; i++)
scanf (“%i”, &mas[i]);
for (i=0; i<10; i++)
if (mas[i]<0 ) { s+=mas[i]; k++};
sa= (float)s/k;
printf (“Середнє арифметичне від’ємних елементів
масиву %f \n”, sa);
printf (“Кількість: %i\n”, k);
}
масиви
Масив, елементи якого є масиви меншої вимірності.
Матриці являють собою порядковий
запис декількох одновимірних масивів. Місце розташування кожного елемента визначається за допомогою двох індексів — номера рядка і номера стовпця, тобто порядкового номера в рядку. Індекси двовимірних масивів записуються в квадратних дужках і нумерація індексів починається з нуля (0).
Двовимірні (і багатовимірні) масиви оголошуються так:
int mas [2] [5] ={ 1, 5, 3, 7, 4,
10, 11, 13, 14, 25 };
int mas [ ][5] ={ 1, 5, 3, 7, 4,
10, 11, 13, 14, 25 };
int mas [ ][5] ={ { 1, 5, 3, 7, 4 },
{10, 11, 13, 14, 25} }
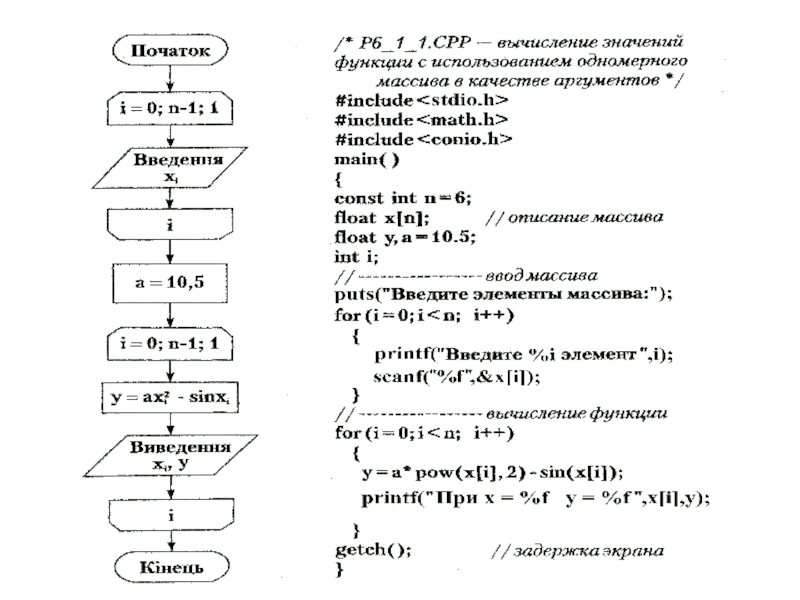
Слайд 7Приклад: Читаючи матрицю по стовпчиках, побудувати
вектор з від’ємних елементів матриці а[3][4] і підрахувати їх
кількість.
#include< stdio.h >
void main()
{
int a[3][4], b[12], i, j, k;
for (i=0; i<3; i++)
for (j=0; j<4; j++)
scanf (“%i”, &a[i][j]);
k=0;
for (j=0; j<4; j++)
for (i=0; i<3; i++)
if (a[i][j]<0) { b[k]=a[i][j];
printf(“b[%i]=%i\n”, k, b[k]);
k++;
}
}
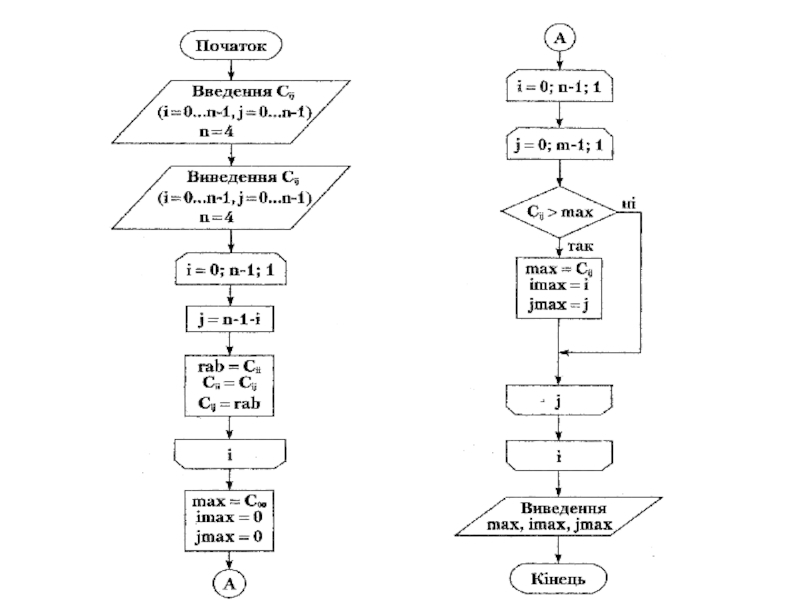
Слайд 9Алгоритми сортування масивів
За принципом дії розрізнятимемо наступні алгоритми:
1. сортування методом
вставки (by insertion);
2. сортування методом вибору (by selection);
3.
сортування методом обміну (by exchange).
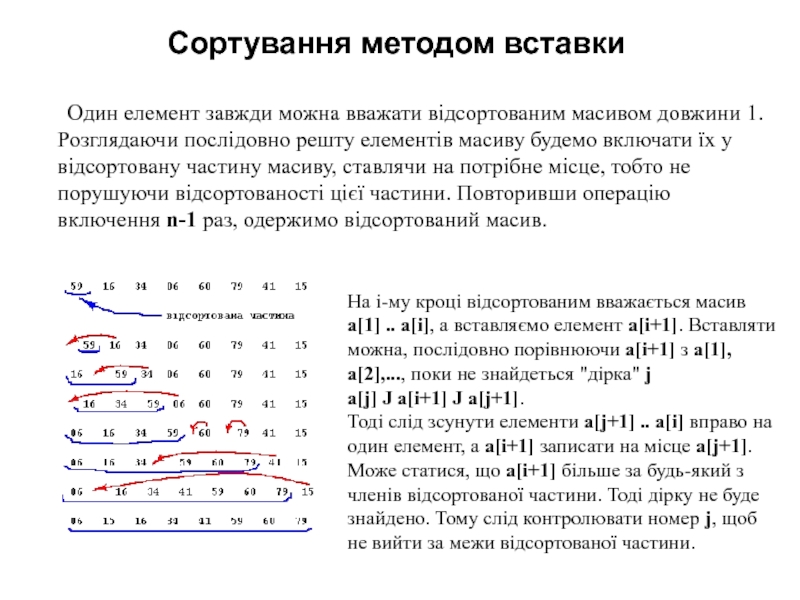
Слайд 10Сортування методом вставки
Один елемент завжди можна вважати відсортованим масивом довжини
1. Розглядаючи послідовно решту елементів масиву будемо включати їх у
відсортовану частину масиву, ставлячи на потрібне місце, тобто не порушуючи відсортованості цієї частини. Повторивши операцію включення n-1 раз, одержимо відсортований масив.
На i-му кроці відсортованим вважається масив a[1] .. a[i], а вставляємо елемент a[i+1]. Вставляти можна, послідовно порівнюючи a[i+1] з a[1], a[2],..., поки не знайдеться "дірка" j
a[j] Ј a[i+1] Ј a[j+1].
Тоді слід зсунути елементи a[j+1] .. a[i] вправо на один елемент, а a[i+1] записати на місце a[j+1].
Може статися, що a[i+1] більше за будь-який з членів відсортованої частини. Тоді дірку не буде знайдено. Тому слід контролювати номер j, щоб не вийти за межи відсортованої частини.
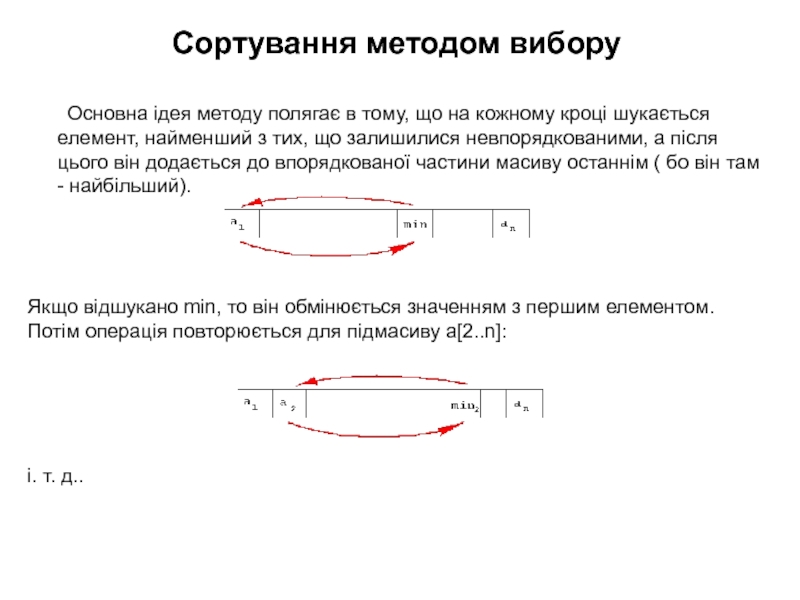
Слайд 11Сортування методом вибору
Основна ідея методу полягає в тому, що на
кожному кроці шукається елемент, найменший з тих, що залишилися невпорядкованими,
а після цього він додається до впорядкованої частини масиву останнім ( бо він там - найбільший).
Якщо відшукано min, то він обмінюється значенням з першим елементом.
Потім операція повторюється для підмасиву a[2..n]:
і. т. д..
Слайд 12Сортування методом обміну
Ідея полягає у тому, щоб на кожному кроці,
порівнюючи сусідні елементи між собою, міняти їх місцями, якщо вони
стоять "не в тому порядку".
Таких проходів по масиву може знадобитися не менше, як (n-1), бо, якщо найменший елемент стоїть на останньому місці, то він досягне свого (першого) місця лише за n-1 крок сусідніх обмінів.
Програма називається "булькове сортування", а метод - методом "бульбашки", бо, якщо вважати кінець масива таким, що знаходиться угорі, то складається враження під час роботи програми, що елементи піднімаються по масиву, як бульбашки у воді до поверхні.

![Масиви [n] = {значення}; [n] = {значення};](/img/thumbs/79874779d1f2d65f737df796b7ed1102-800x.jpg)



![Масиви Приклад: Читаючи матрицю по стовпчиках, побудувати вектор з від’ємних Приклад: Читаючи матрицю по стовпчиках, побудувати вектор з від’ємних елементів матриці а[3][4]](/img/thumbs/53e9ad99bfc1ee932271dee6bf2b7370-800x.jpg)