Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика
Содержание
- 1. Математическая логика
- 2. Математическая логика§ 5. Логика и компьютер
- 3. Логика, высказыванияЛогика (др.греч. λογικος) – это наука
- 4. Высказывание или нет?Сейчас идет дождь.Жирафы летят на
- 5. Логика и компьютерЛогика изучает операции между 0
- 6. Простые и составные высказыванияA – Сейчас идет
- 7. Операция НЕ (инверсия)Если высказывание A истинно, то
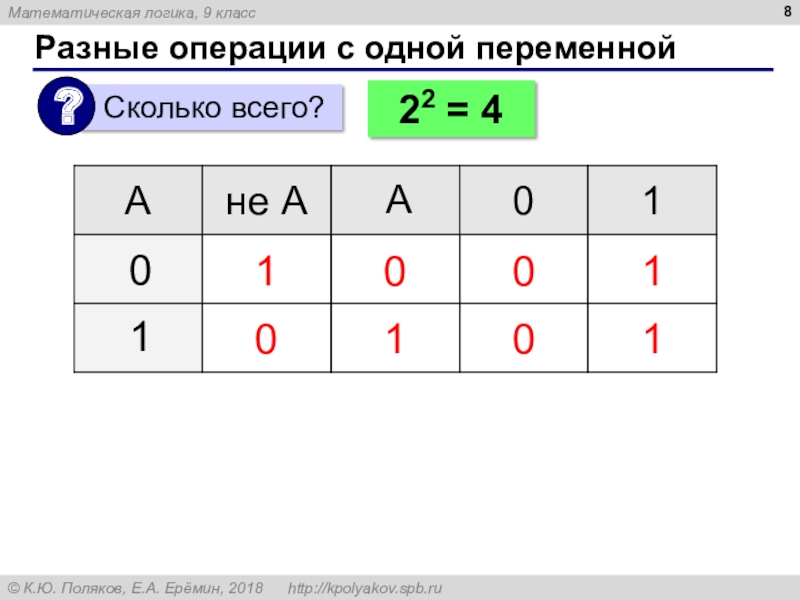
- 8. Разные операции с одной переменной100110А001122 = 4
- 9. Операция ИВысказывание «A и B» истинно тогда
- 10. Операция И (логическое умножение, конъюнкция)10также A·B, A
- 11. Операция ИЛИ (логическое сложение, дизъюнкция)Высказывание «A или
- 12. Операция ИЛИ (логическое сложение, дизъюнкция)10также: A+B, A
- 13. Упрощение логических выраженийA и 0 = A
- 14. Математическая логика§ 6. Логические элементы
- 15. Элемент «НЕ»значок инверсии??не Aне A
- 16. Элементы «И» и «ИЛИ»A и BA или BДвойные элементы:«ИЛИ-НЕ»«И-НЕ»не (A и B)не (A или B)«И»«ИЛИ»
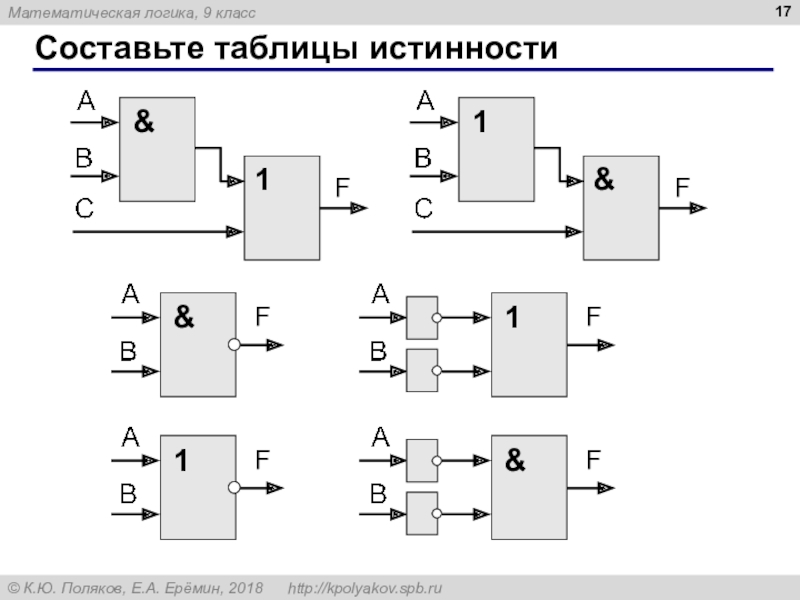
- 17. Составьте таблицы истинности
- 18. Математическая логика§ 7. Другие логические операции
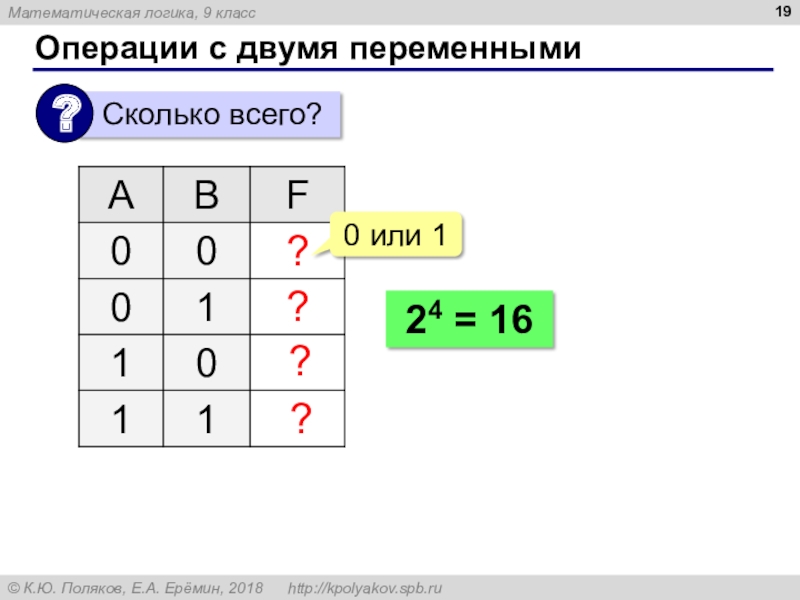
- 19. Операции с двумя переменными????0 или 124 = 16
- 20. ИмпликацияX = Если идёт дождь, то
- 21. Постройте таблицы истинностиB A A BX = B A
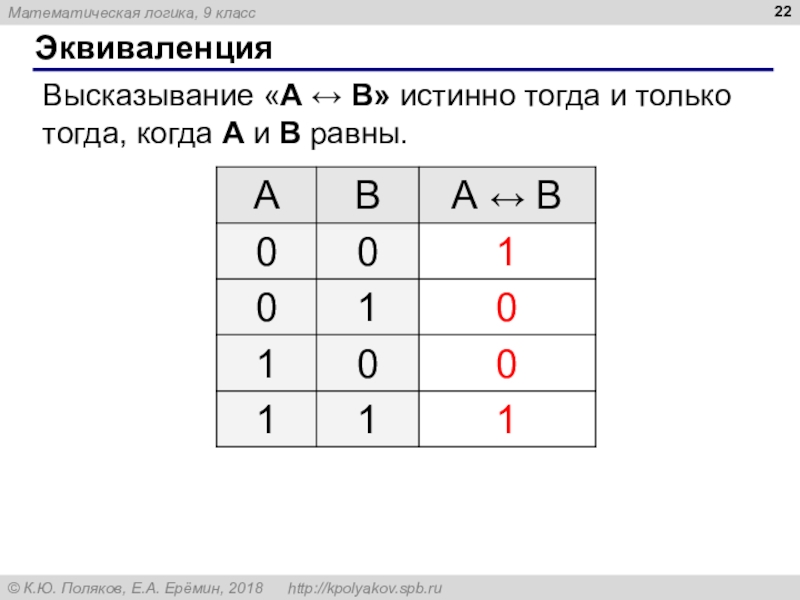
- 22. ЭквиваленцияВысказывание «A B» истинно тогда и только тогда, когда А и B равны.
- 23. Постройте таблицы истинности
- 24. Исключающее «ИЛИ»Высказывание «A B» истинно тогда,
- 25. Постройте таблицы истинности
- 26. Упрощение логических выраженийA 0 =A
- 27. Шифрование(A B) B = A
- 28. Математическая логика§ 8. Логические выражения
- 29. Логические выраженияЛогическое выражение — это выражение, результат
- 30. Порядок вычисленияскобкиНЕИИЛИимпликацияэквиваленция123456, исключающее ИЛИ
- 31. Таблицы истинностиЛогические выражения могут быть:вычислимыми (зависят от
- 32. Таблицы истинностиЕсли два выражения принимают одинаковые значения
- 33. Неполные таблицы истинности23 = 8один ноль в таблицепо 1-й строкепо 2-й строке25 = 32
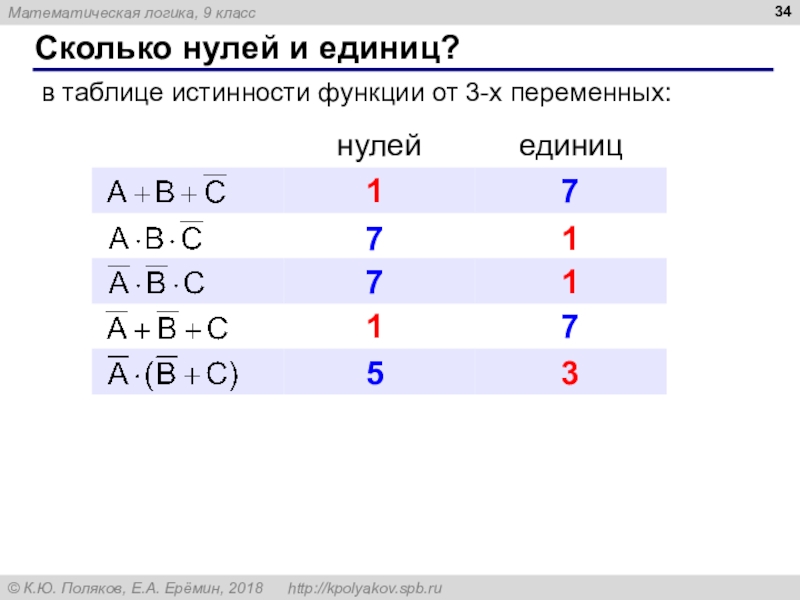
- 34. Сколько нулей и единиц?в таблице истинности функции от 3-х переменных:1771711753
- 35. Неполные таблицы истинностиодин ноль, две единицыпо 1-й строкепо 2-й строкетолько 1 единица,все строки разные!
- 36. Составление условий(x 3) и (x
- 37. Составление условийлевая граница:x – 1нижняя граница:y
- 38. Составление условий(x2+y2 1)и (x 0)леваяправая(x 0)и (x2+y2 1)леваянижняяи (y – x)верхняя
- 39. Составление условий=+((x2+y2 1) и (x
- 40. Определение истинности выраженийДля каких из указанных значений
- 41. Табличный методДля каких из указанных значений числа
- 42. ЗадачиДля каких из указанных значений числа X
- 43. ЗадачиДля каких значений числа X истинно высказывание:(X
- 44. ЗадачиДля каких из приведённых имён ЛОЖНО высказывание:НЕ(Первая
- 45. ЗадачиДля каких из приведённых имён ЛОЖНО высказывание:НЕ(Первая
- 46. ЗадачиДля каких из приведённых имён ЛОЖНО высказывание:НЕ(Первая
- 47. ЗадачиДля каких значений числа X ЛОЖНО высказывание:(НЕ
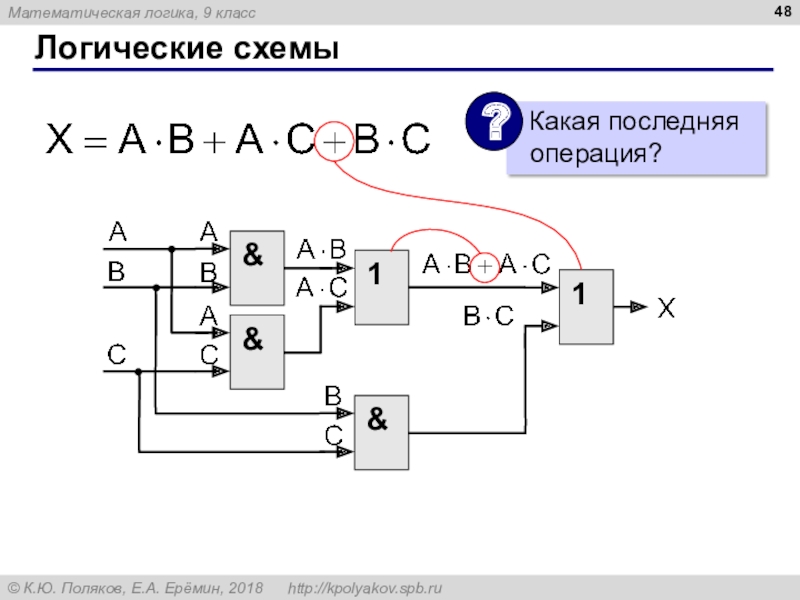
- 48. Логические схемы
- 49. Математическая логика§ 12. Множества и логика
- 50. Что такое множество?Множество – некоторый набор элементов,
- 51. Изображение множествДиаграммы Эйлера-ВеннаA и BA или B(не
- 52. Количество элементов множествПоисковые запросы в Интернете:
- 53. ЗадачиВ таблице приведены запросы к поисковому серверу.
- 54. Использование диаграммпринтерысканерыпродажапринтеры & сканеры & продажа
- 55. ЗадачиВ таблице приведены запросы к поисковому серверу.
- 56. Количество элементов множествИзвестно количество сайтов, которых находит
- 57. Количество элементов множествABВ общем виде:NA&B = ?0NA
- 58. Задачи с тремя областямиИзвестно количество сайтов, которых
- 59. Задача с тремя областямисобакикошкилемурыB = кошки &
- 60. Задачи с тремя областямиИзвестно количество сайтов, которых
- 61. Известно количество сайтов, которых находит поисковый сервер
- 62. Задачи с тремя областямиА (сканер)B (принтер)NA|B =
- 63. Конец фильмаПОЛЯКОВ Константин Юрьевичд.т.н., учитель информатикиГБОУ СОШ
- 64. Источники иллюстрацийиллюстрации художников издательства «Бином»авторские материалы
- 65. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математическая логика
§ 8. Логика и компьютеры
§ 9. Логические элементы
§ 10.
Другие логические операции
Слайд 3Логика, высказывания
Логика (др.греч. λογικος) – это наука о том, как
правильно рассуждать, делать выводы, доказывать утверждения.
Формальная логика отвлекается от конкретного
содержания, изучает только истинность и ложность высказываний. Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.
Слайд 4Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный
предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N
живут 2 миллиона человек.Который час?
Слайд 5Логика и компьютер
Логика изучает операции между 0 и 1!
Джордж Буль
Алгебра
логики — это математический аппарат, с помощью которого записывают, упрощают
и преобразуют логические высказывания, вычисляют их значения.Алгебра высказываний,
булева алгебра
двоичная логика
Слайд 6Простые и составные высказывания
A – Сейчас идет дождь.
B – Форточка
открыта.
простые высказывания (элементарные)
Составные высказывания строятся из простых с помощью логических
связок (операций) «и», «или», «не», «если … то», «тогда и только тогда» и др. A и B
A или не B
если A, то B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
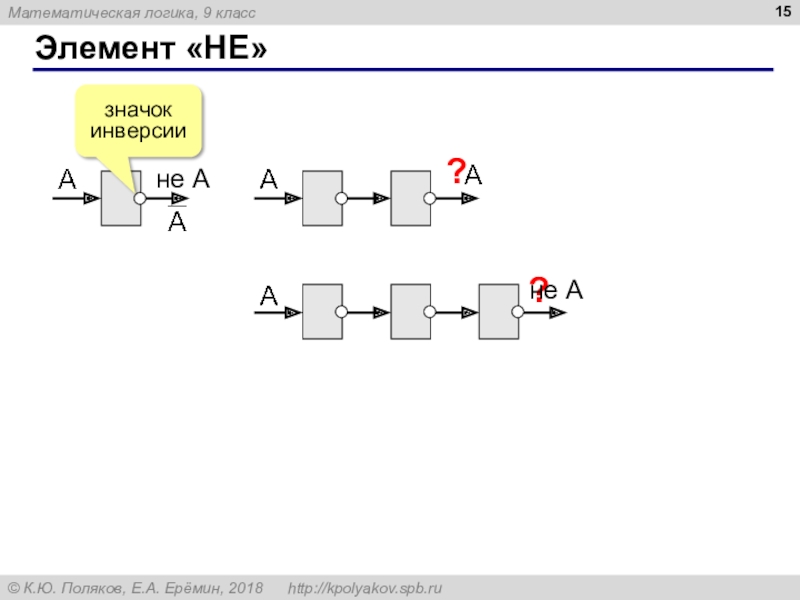
Слайд 7Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно,
и наоборот.
1
0
0
1
таблица истинности операции НЕ
Таблица истинности логического выражения Х –
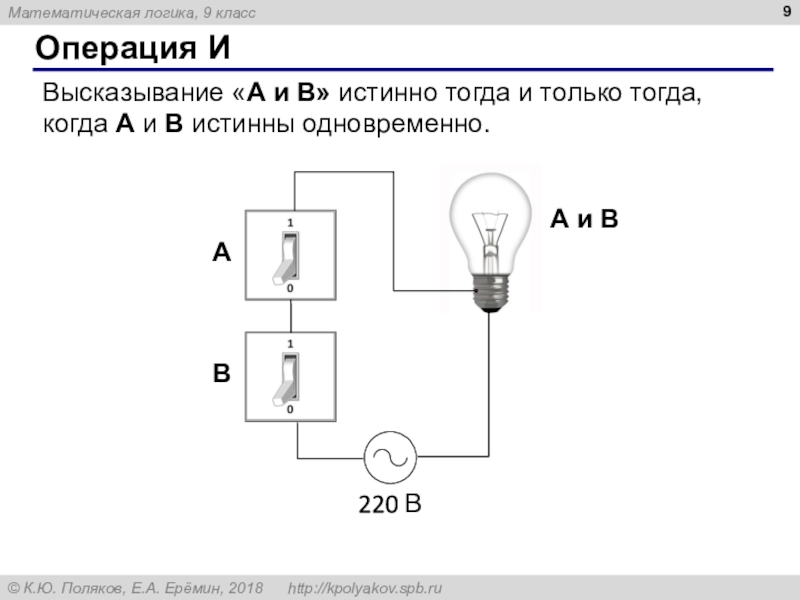
это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.Слайд 9Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
A и B
A
B
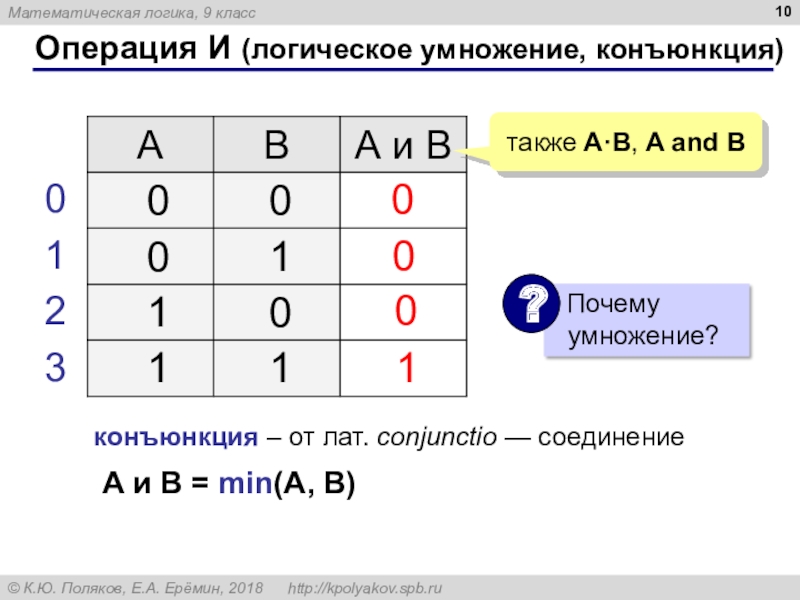
Слайд 10Операция И (логическое умножение, конъюнкция)
1
0
также A·B, A and B
0
0
конъюнкция –
от лат. conjunctio — соединение
A и B = min(A,
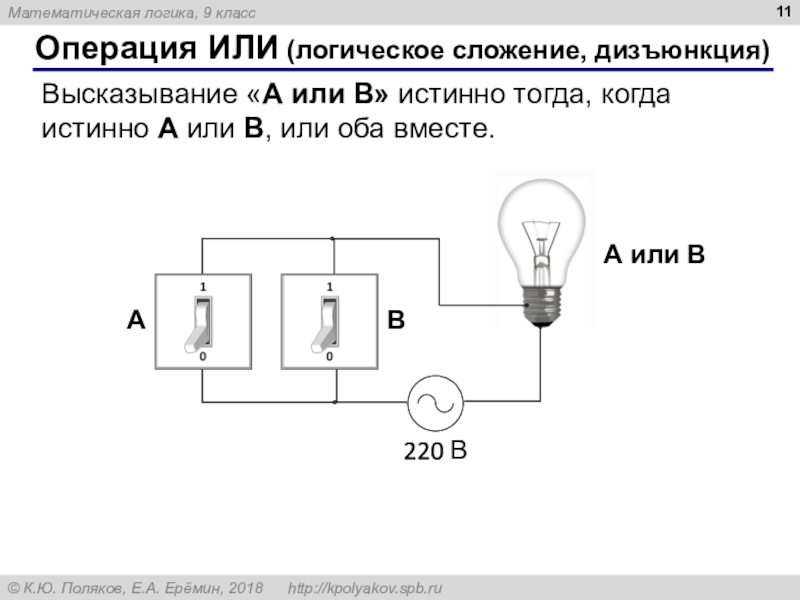
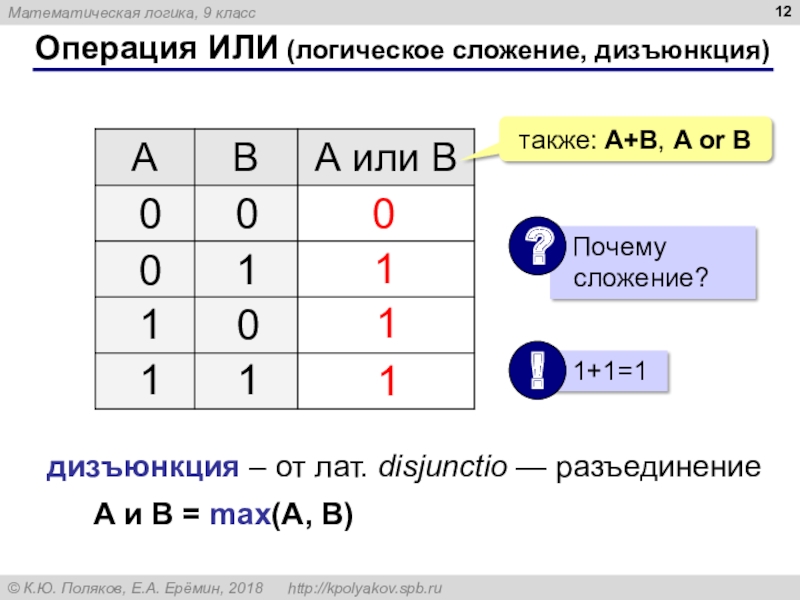
B)Слайд 11Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда,
когда истинно А или B, или оба вместе.
A или B
A
B
Слайд 12Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
также: A+B, A or B
1
1
дизъюнкция –
от лат. disjunctio — разъединение
A и B = max(A,
B)Слайд 13Упрощение логических выражений
A и 0 = A ∙ 0 =
A
и 1 = A ∙ 1 =
A
0
A или 0 =
A + 0 =A или 1 = A + 1 =
1
A
A и не A = A ∙ A =
A или (не A) = A + A =
0
1
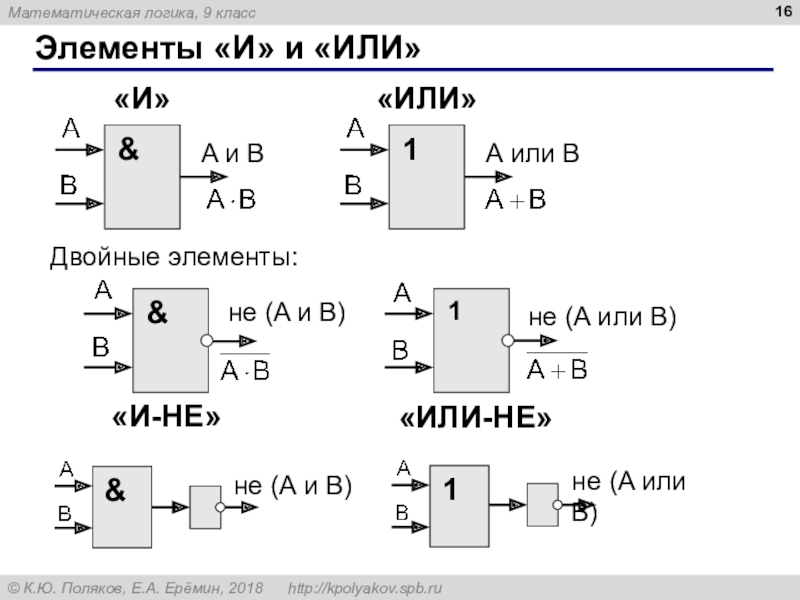
Слайд 16Элементы «И» и «ИЛИ»
A и B
A или B
Двойные элементы:
«ИЛИ-НЕ»
«И-НЕ»
не (A
и B)
не (A или B)
«И»
«ИЛИ»
Слайд 20Импликация
X = Если идёт дождь, то
Лена раскрывает зонтик.
X = A
BИмпликация A → B истинна, если не исключено, что из A следует B.
1
1
0
1
Идёт дождь, но Лена не раскрыла зонтик.
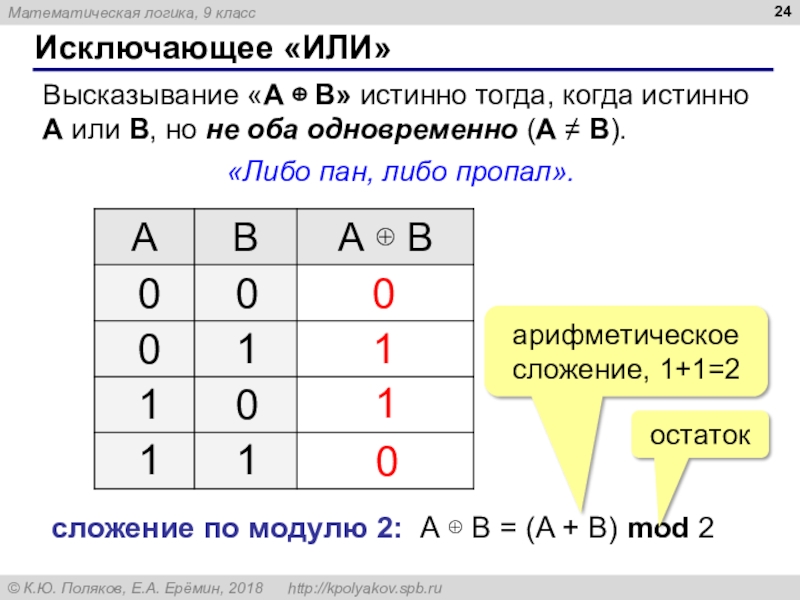
Слайд 24Исключающее «ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
или B, но не оба одновременно (A B).
«Либо пан,
либо пропал».0
0
1
1
сложение по модулю 2: А B = (A + B) mod 2
арифметическое сложение, 1+1=2
остаток
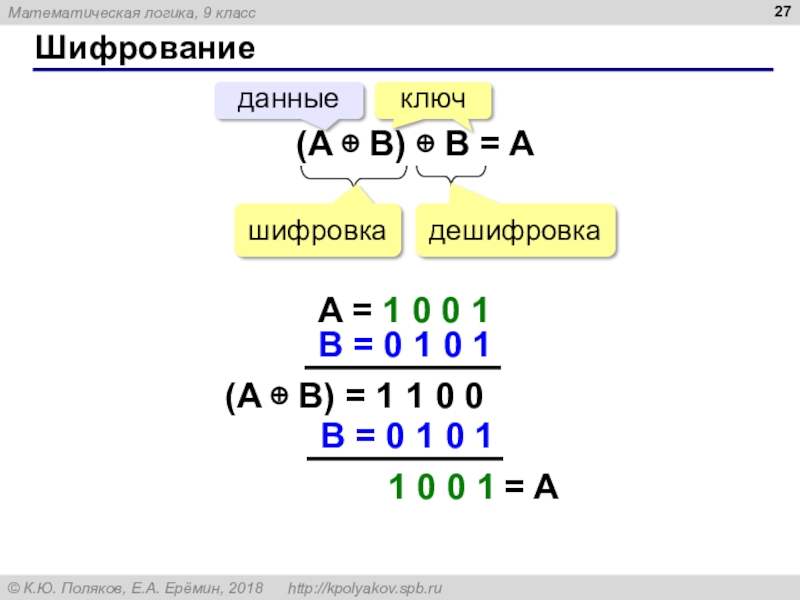
Слайд 27Шифрование
(A B) B = A
данные
шифровка
дешифровка
A = 1
0 0 1
B = 0 1 0 1
(A
B) = 1 1 0 0 B = 0 1 0 1
1 0 0 1
= A
Слайд 29Логические выражения
Логическое выражение — это выражение, результат вычисления которого —
логическое значение (истина или ложь).
Авария = вышли из строя 2
из 3-х двигателей.A – «Двигатель № 1 неисправен».
B – «Двигатель № 2 неисправен».
C – «Двигатель № 3 неисправен».
Аварийный сигнал:
X = «Неисправны два двигателя»
= (A и B) или (A и C) или (B и C)
логическое выражение
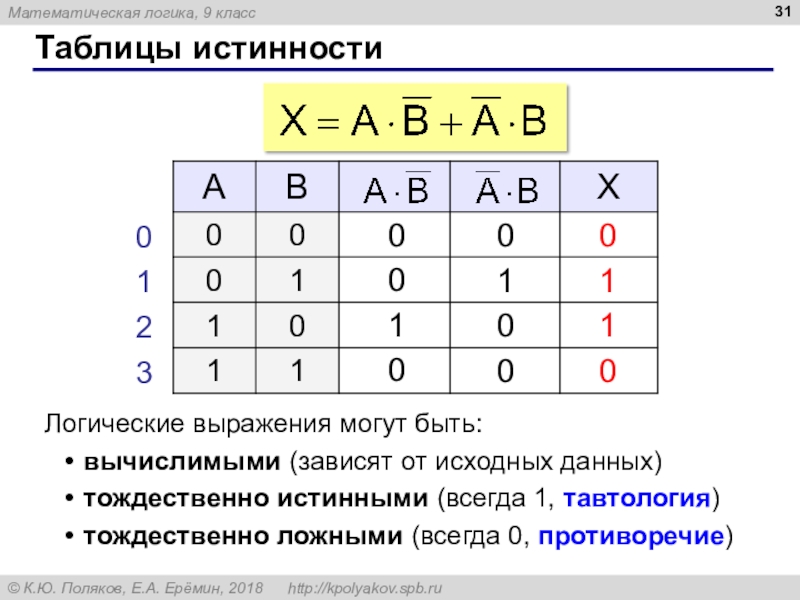
Слайд 31Таблицы истинности
Логические выражения могут быть:
вычислимыми (зависят от исходных данных)
тождественно истинными
(всегда 1, тавтология)
тождественно ложными (всегда 0, противоречие)
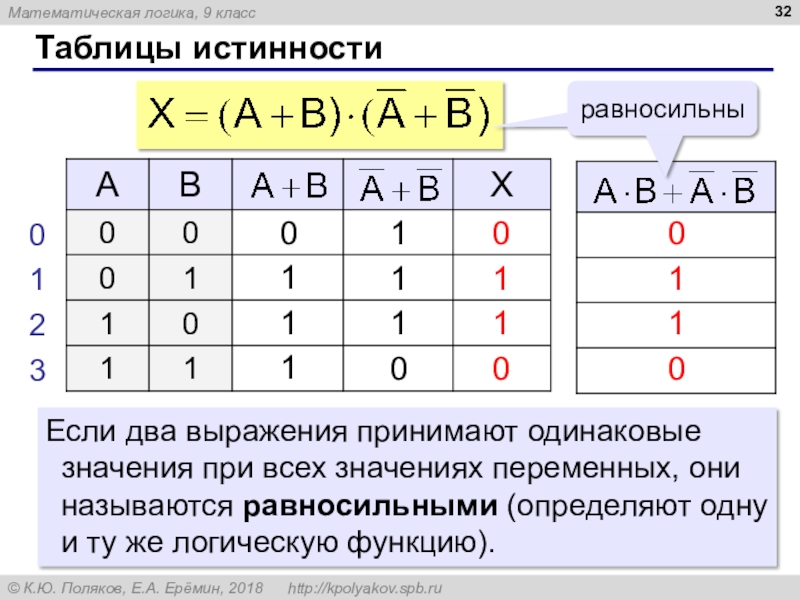
Слайд 32Таблицы истинности
Если два выражения принимают одинаковые значения при всех значениях
переменных, они называются равносильными (определяют одну и ту же логическую
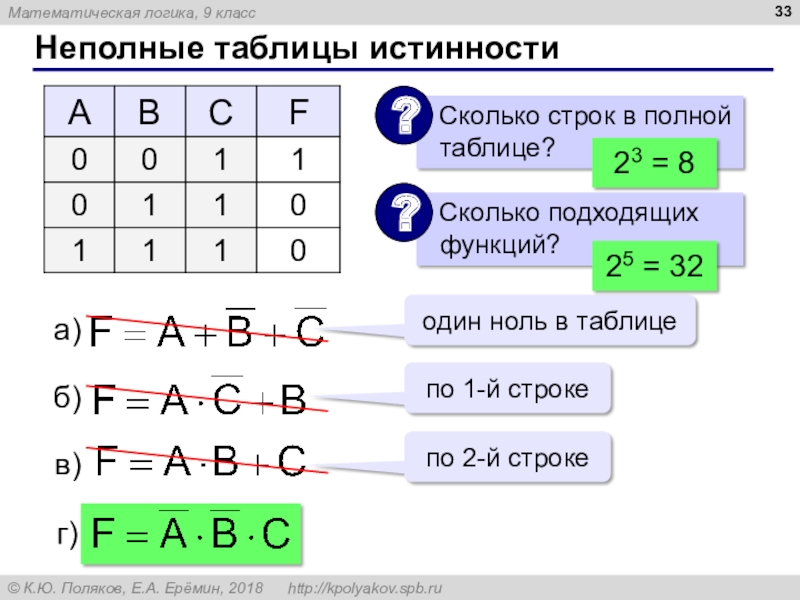
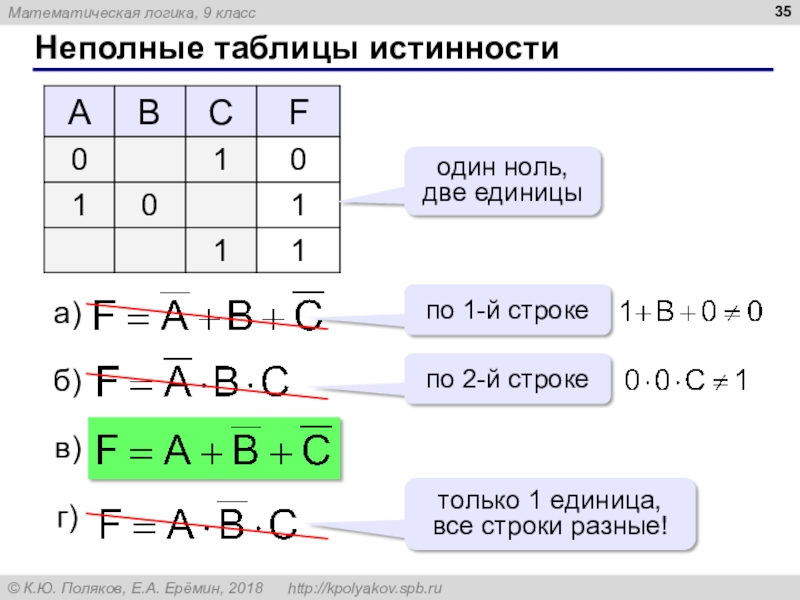
функцию).Слайд 35Неполные таблицы истинности
один ноль,
две единицы
по 1-й строке
по 2-й строке
только
1 единица,
все строки разные!
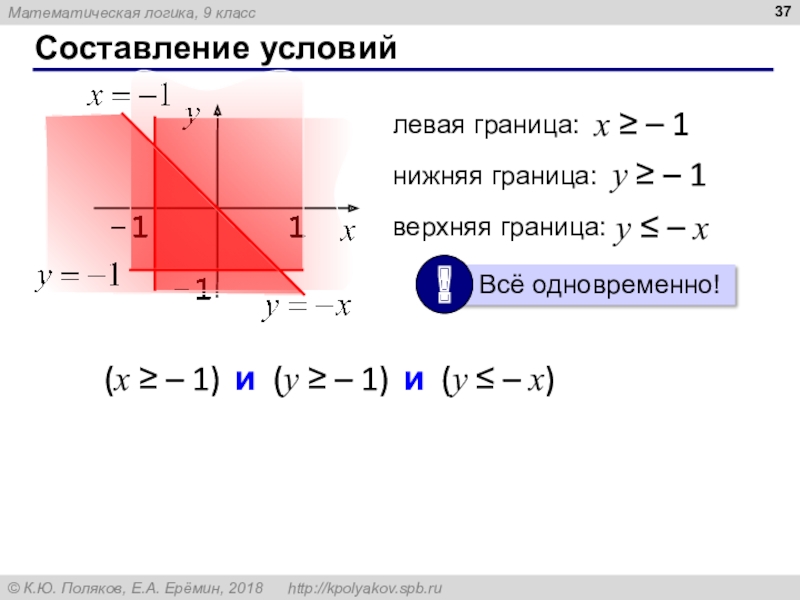
Слайд 36Составление условий
(x 3) и (x 6)
(3 x)
и (x 6)
(1 x) и (x 3)
или (5 x) и (x 8)Слайд 37Составление условий
левая граница:
x – 1
нижняя граница:
y – 1
верхняя
граница:
y – x
(x – 1)
и (y –
1)и (y – x)
Слайд 38Составление условий
(x2+y2 1)
и (x 0)
левая
правая
(x 0)
и (x2+y2
1)
левая
нижняя
и (y – x)
верхняя
Слайд 40Определение истинности выражений
Для каких из указанных значений числа X истинно
высказывание:
(X
< 5) И НЕ (X < 1) ? X = 2:
( 1 ) И НЕ ( 0 )
X = 4:
( 1 ) И НЕ ( 0 )
X = 8:
( 0 ) И НЕ ( 0 )
( 0 И 1)
= 0
( 1 И 1 )
= 1
( 1 И 1 )
= 1
можно не вычислять!
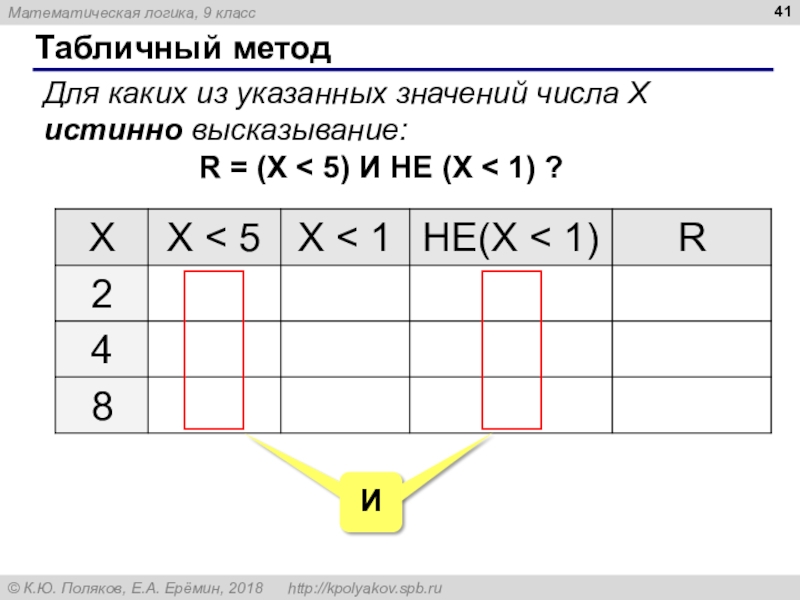
Слайд 41Табличный метод
Для каких из указанных значений числа X истинно высказывание:
R =
(X < 5) И НЕ (X < 1) ?Слайд 42Задачи
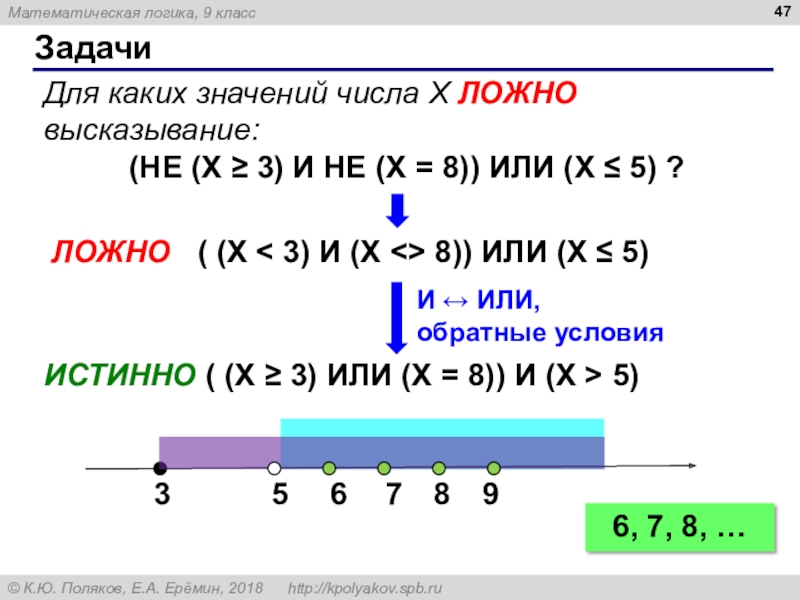
Для каких из указанных значений числа X ЛОЖНО высказывание:
(НЕ (X
≥ 3) И НЕ (X = 8)) ИЛИ (X ≤
5) ?X = 4:
(НЕ (1) И НЕ (0)) ИЛИ (1)
= 1
X = 1:
(НЕ (0) И НЕ (0)) ИЛИ (1)
= 1
X = 8:
(НЕ (1) И НЕ (1)) ИЛИ (0)
( 0 И 0 ) ИЛИ (0)
= 0
? + 1
Слайд 43Задачи
Для каких значений числа X истинно высказывание:
(X < 5) И
НЕ (X < 1) ?
(X < 5) И (X
>= 1) 1, 2, 3, 4
Слайд 44Задачи
Для каких из приведённых имён ЛОЖНО высказывание:
НЕ(Первая буква гласная) ИЛИ
(Последняя буква гласная) ?
(Первая буква согласная)
Слайд 45Задачи
Для каких из приведённых имён ЛОЖНО высказывание:
НЕ(Первая буква гласная) ИЛИ
(Последняя буква гласная) ?
(Первая буква согласная) ИЛИ
(Последняя буква гласная)
Никита
Антон
Даниил
Инна
Кирилл
Егор
Мефодий
Игнат
ЛОЖНО
A + B = 0
ИЛИ И,
обратные условия
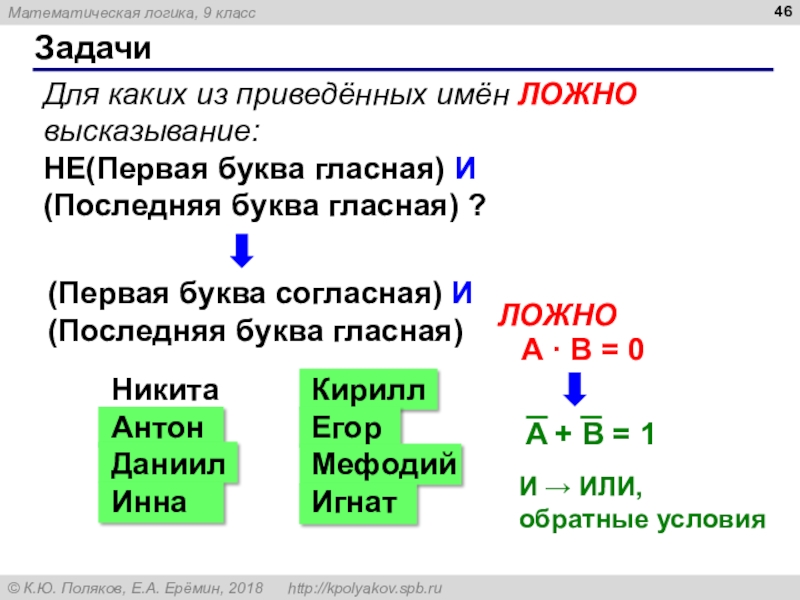
Слайд 46Задачи
Для каких из приведённых имён ЛОЖНО высказывание:
НЕ(Первая буква гласная) И
(Последняя буква гласная) ?
(Первая буква согласная) И
(Последняя буква гласная)
Никита
Антон
Даниил
Инна
Кирилл
Егор
Мефодий
Игнат
ЛОЖНО
A · B = 0
И ИЛИ,
обратные условия
Слайд 47Задачи
Для каких значений числа X ЛОЖНО высказывание:
(НЕ (X ≥ 3)
И НЕ (X = 8)) ИЛИ (X ≤ 5) ?
ЛОЖНО ( (X < 3) И (X <> 8)) ИЛИ (X ≤ 5)
6, 7, 8, …
ИСТИННО ( (X ≥ 3) ИЛИ (X = 8)) И (X > 5)
И ИЛИ,
обратные условия
Слайд 50Что такое множество?
Множество – некоторый набор элементов, каждый из которых
отличается от остальных.
пустое множество:
конечное число элементов: буквы русского алфавита
бесконечное
число элементов: натуральные числаКак задать множество?
перечислением элементов
{Вася, Петя, Коля}
логическим выражением:
{x: x > 0}
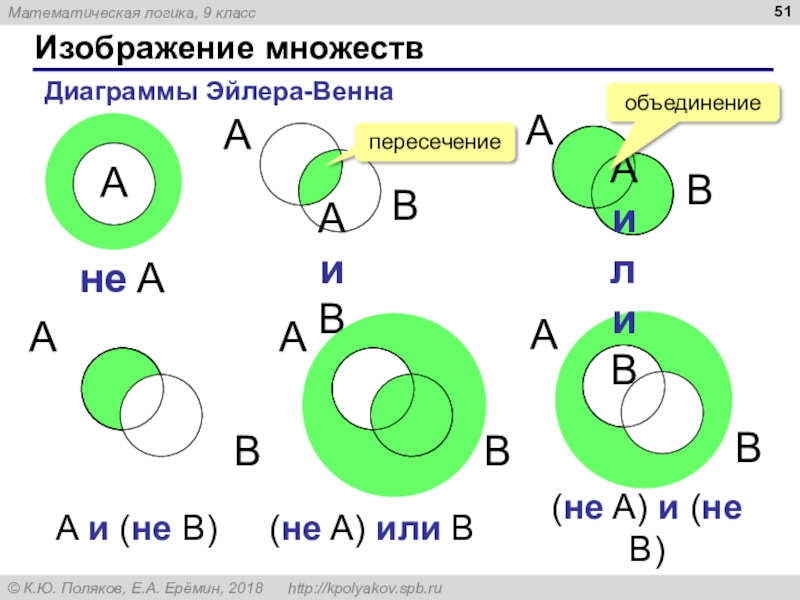
Слайд 51Изображение множеств
Диаграммы Эйлера-Венна
A и B
A или B
(не A) или B
пересечение
объединение
A
и (не B)
не A
(не A) и (не B)
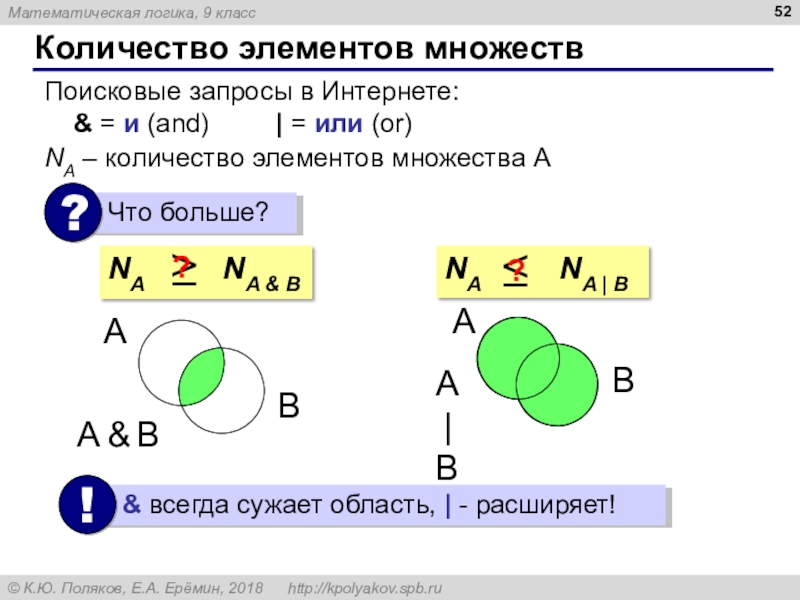
Слайд 52Количество элементов множеств
Поисковые запросы в Интернете:
& = и
(and) | = или (or)
NA –
количество элементов множества ANA NA & B
?
NA NA | B
?
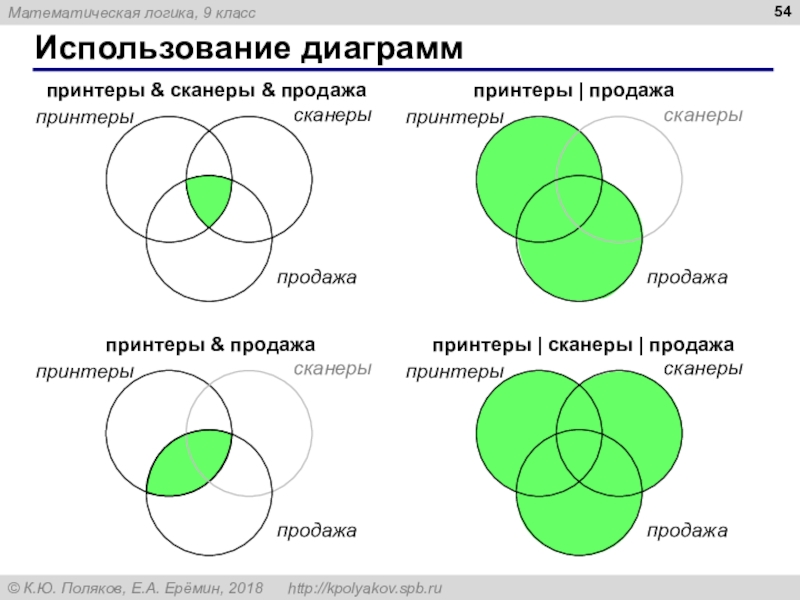
Слайд 53Задачи
В таблице приведены запросы к поисковому серверу. Расположите номера запросов
в порядке возрастания количества страниц, которые найдет поисковый сервер по
каждому запросу.А: принтеры & сканеры & продажа
Б: принтеры | продажа
В: принтеры & продажа
Г: принтеры | сканеры | продажа
АВБГ
Слайд 55Задачи
В таблице приведены запросы к поисковому серверу. Расположите номера запросов
в порядке убывания количества страниц, которые найдет поисковый сервер по
каждому запросу.А: принтеры & сканеры & продажа
Б: (принтеры & сканеры) | продажа
В: (принтеры | сканеры) & продажа
Г: принтеры | сканеры | продажа
ГБВА
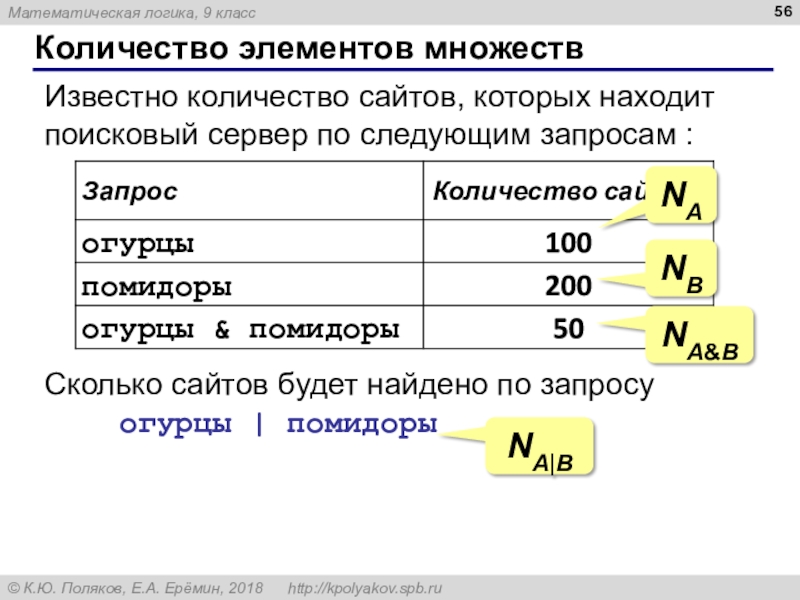
Слайд 56Количество элементов множеств
Известно количество сайтов, которых находит поисковый сервер по
следующим запросам :
Сколько сайтов будет найдено по запросу
огурцы | помидорыNA
NB
NA&B
NA|B
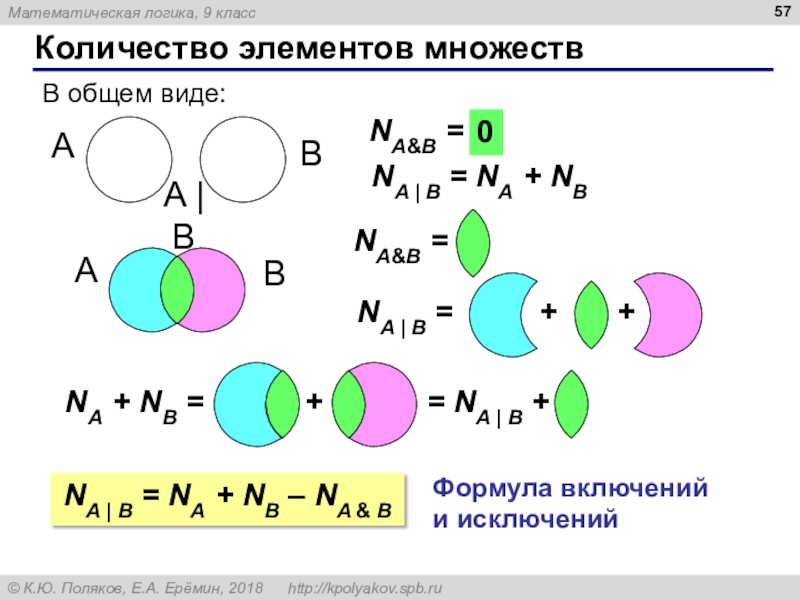
Слайд 57Количество элементов множеств
A
B
В общем виде:
NA&B = ?
0
NA | B =
NA + NB
A
B
NA | B =
+ + NA + NB =
NA&B =
NA | B = NA + NB – NA & B
Формула включений
и исключений
+ = NA | B +
A | B
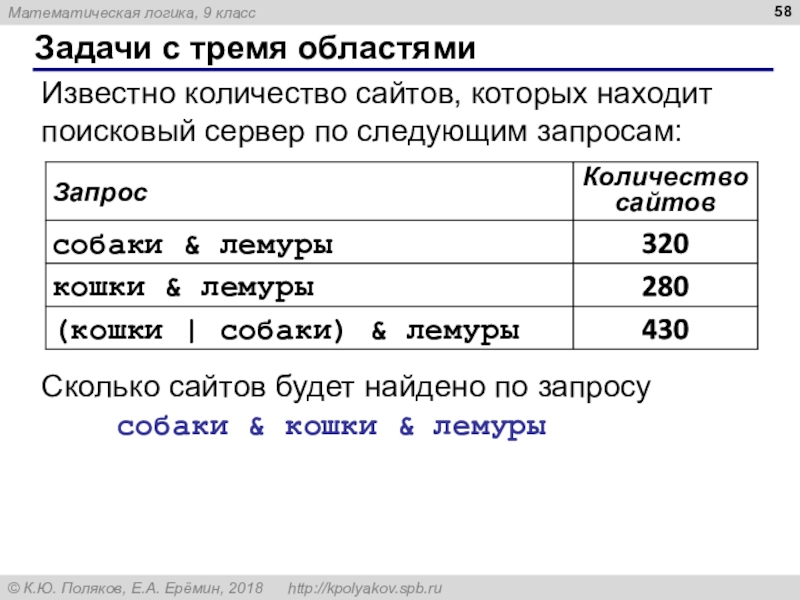
Слайд 58Задачи с тремя областями
Известно количество сайтов, которых находит поисковый сервер
по следующим запросам:
Сколько сайтов будет найдено по запросу
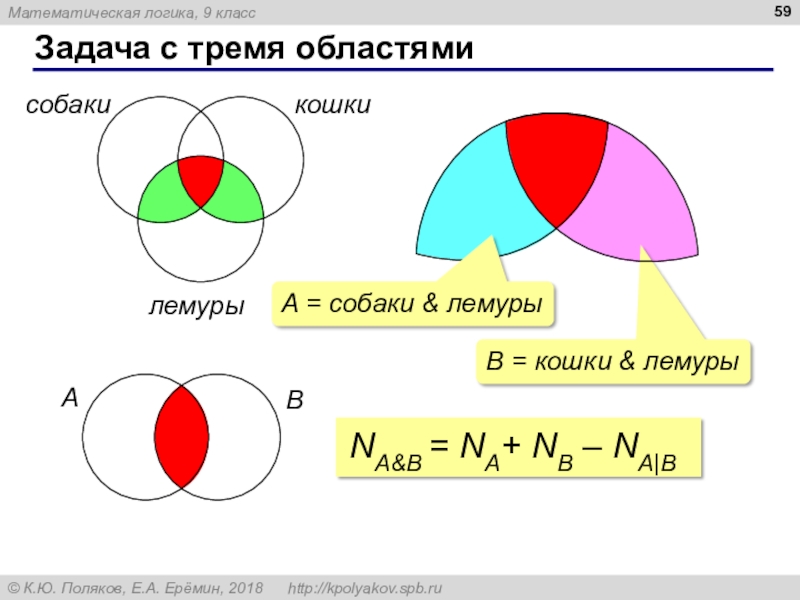
собаки & кошки & лемурыСлайд 59Задача с тремя областями
собаки
кошки
лемуры
B = кошки & лемуры
A
B
NA&B = NA+
NB – NA|B
A = собаки & лемуры
Слайд 60Задачи с тремя областями
Известно количество сайтов, которых находит поисковый сервер
по следующим запросам:
Сколько сайтов будет найдено по запросу
собаки & кошки & лемурыA
B
A | B
A & B
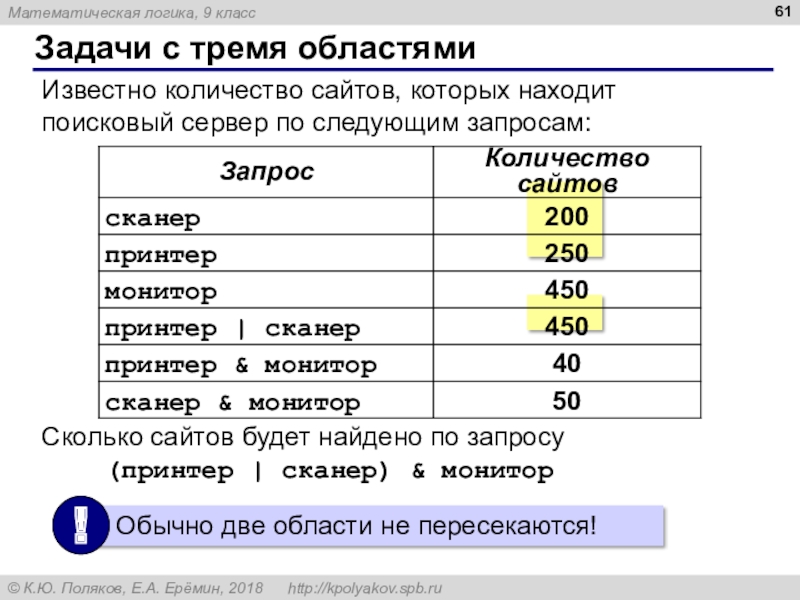
Слайд 61Известно количество сайтов, которых находит поисковый сервер по следующим запросам:
Сколько
сайтов будет найдено по запросу
(принтер | сканер)
& мониторЗадачи с тремя областями
Слайд 62Задачи с тремя областями
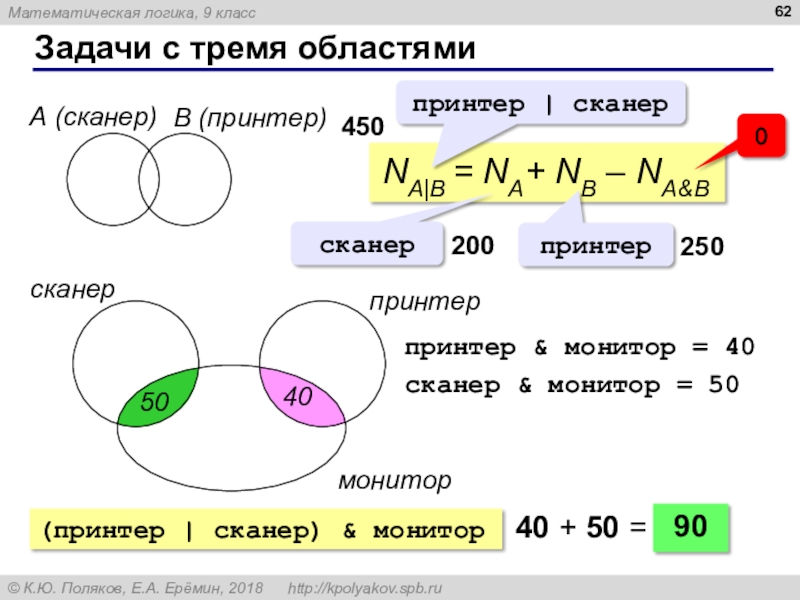
А (сканер)
B (принтер)
NA|B = NA+ NB –
NA&B
принтер | сканер
450
сканер
принтер
200
250
0
сканер
принтер
монитор
90
40 + 50 =
принтер & монитор =
40 сканер & монитор = 50
50
40
(принтер | сканер) & монитор
Слайд 63Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г.
Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО
ПГГПУ, г. Пермьeremin@pspu.ac.ru