Слайд 1Математические методы
(Исследование операций, Методы оптимизации)
Задача о максимальном потоке
Слайд 3Постановка задачи
Рассмотрим сеть трубопроводов для транспортировки сырой нефти от буровых
скважин до нефтеперегонных заводов.
Для перекачки нефти предусмотрены магистральные насосные
станции. Каждый сегмент трубопровода имеет свою пропускную способность.
Сегменты трубопровода могут быть как однонаправленные (осуществляют перекачку нефти только в одном направлении), так и в двунаправленные.
Слайд 4Постановка задачи
В однонаправленных сегментах положительная пропускная способность предполагается в одном
направлении и нулевая - в другом. Как определить оптимальную пропускную
способность (т.е. максимальный поток) между нефтяными скважинами и нефтеперегонными заводами?
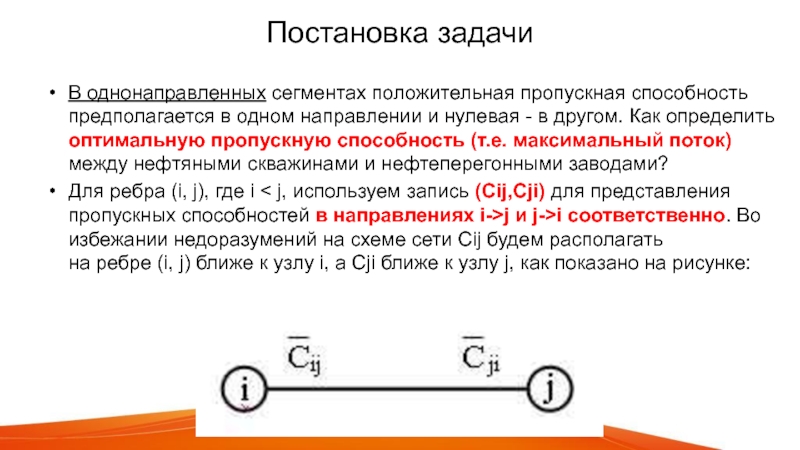
Для ребра (i, j), где i < j, используем запись (Cij,Cji) для представления пропускных способностей в направлениях i->j и j->i соответственно. Во избежании недоразумений на схеме сети Cij будем располагать
на ребре (i, j) ближе к узлу i, а Cji ближе к узлу j, как показано на рисунке:
Слайд 5Основные определения
Разрез определяет множество ребер, при удалении которых из сети
полностью прекращается поток от источника к столу. Пропускная способность разреза
равна сумме пропускных способностей "разрезанных" ребер. Среди всех разрезов сети разрез с минимальной пропускной способностью определяет максимальный поток в сети.
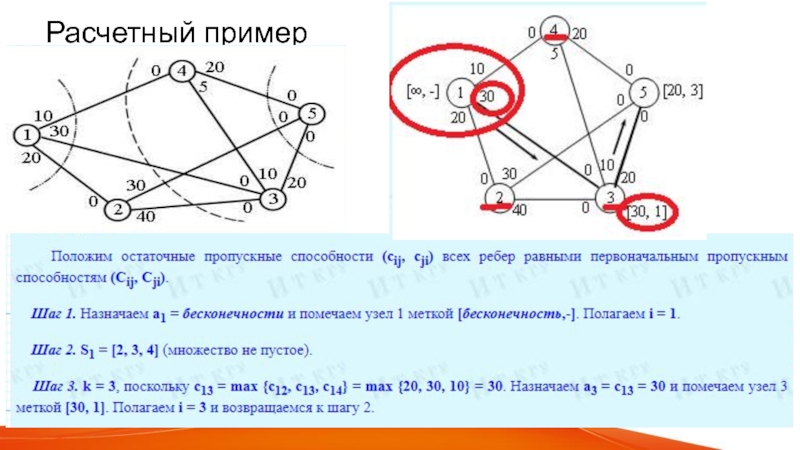
Слайд 6Пример
Рассмотрим сеть, показанную на рис. 3. На этом рисунке при
обозначении пропускных способностей двунаправленных ребер придерживались соглашения, принятого ранее (рис.
2). Например, для ребра (3, 4) пропускная способность в направлении 3 -> 4 равна 10, а в направлении 4 -> 3 равна 5.
Слайд 7Переход к алгоритму
Вывод, который можно сделать из этих трех разрезов,
заключается в том, что максимальный поток не может превышать 60
единиц (минимальное число).
Но мы не можем сказать, какой максимальный поток на самом деле, так как не перебрали все возможные разрезы сети.
К сожалению, перебор всех разрезов является непростой задачей. Поэтому для определения максимального потока в сети не используются алгоритмы, основанные на полном переборе разрезов.
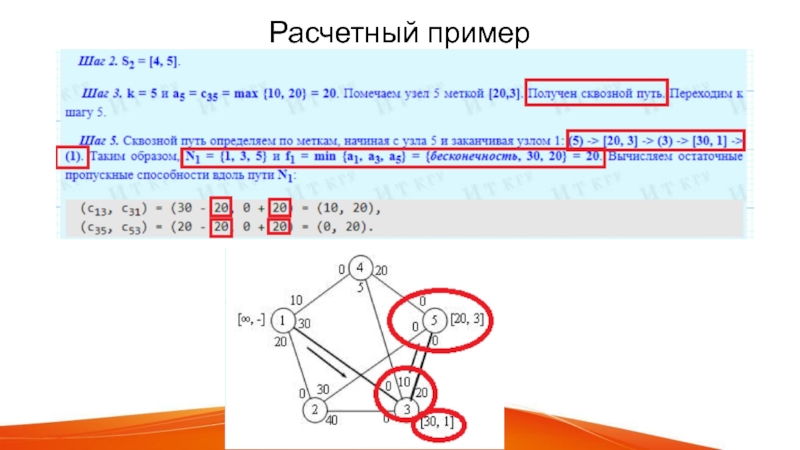
Слайд 8Идея алгоритма нахождения максимального потока
Идея данного алгоритма состоит в нахождении
сквозных путей с положительными потоками от источника к стоку.
Рассмотрим ребро
(i, j) с (начальной) пропускной способностью (Cij,Cji). В процессе выполнения алгоритма части этих пропускных способностей "забираются" потоками, проходящими через данное ребро, в результате каждое ребро будет иметь остаточную пропускную способность. Будем использовать запись (cij, cji) для представления остаточных пропускных способностей. Сеть, где все ребра имеют остаточную пропускную способность, назовем остаточной.
Для произвольного узла j, получающего поток от узла i, определим метку [aj, i], где aj - величина потока, протекающего от узла j к узлу i. Алгоритм нахождения максимального потока предполагает выполнение следующих действий.
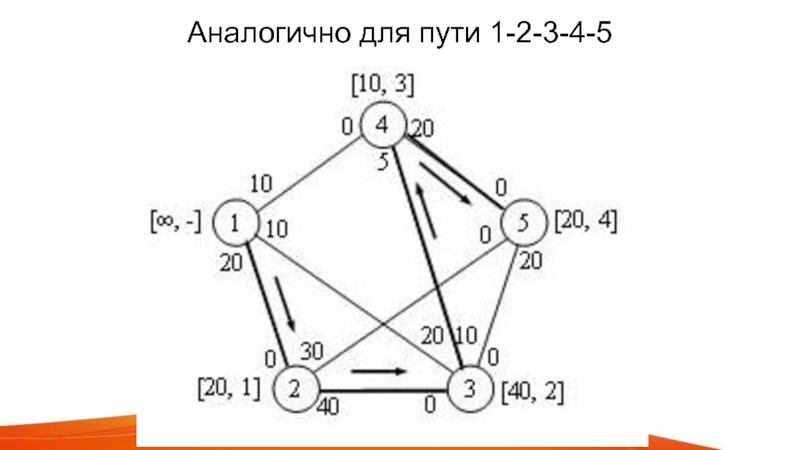
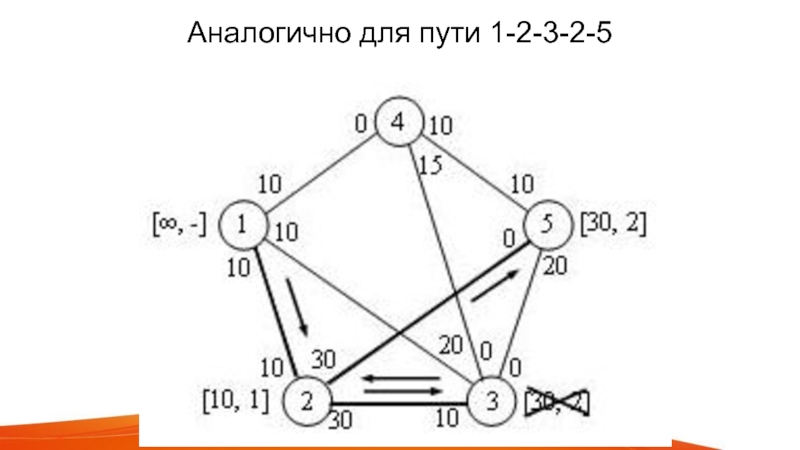
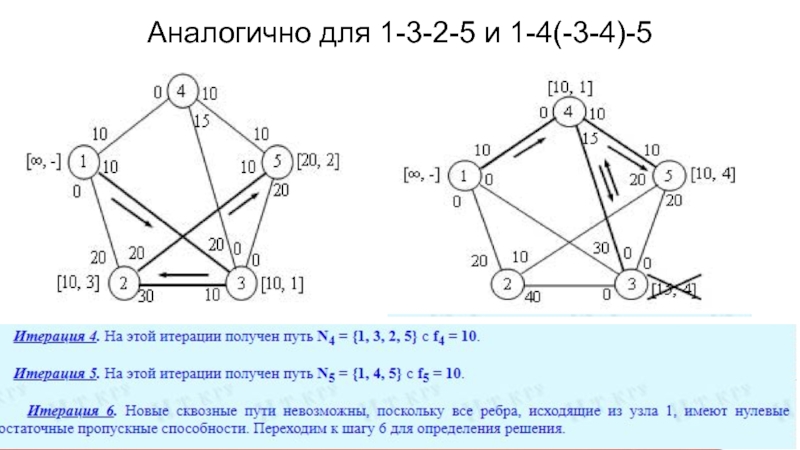
Слайд 19Аналогично для 1-3-2-5 и 1-4(-3-4)-5