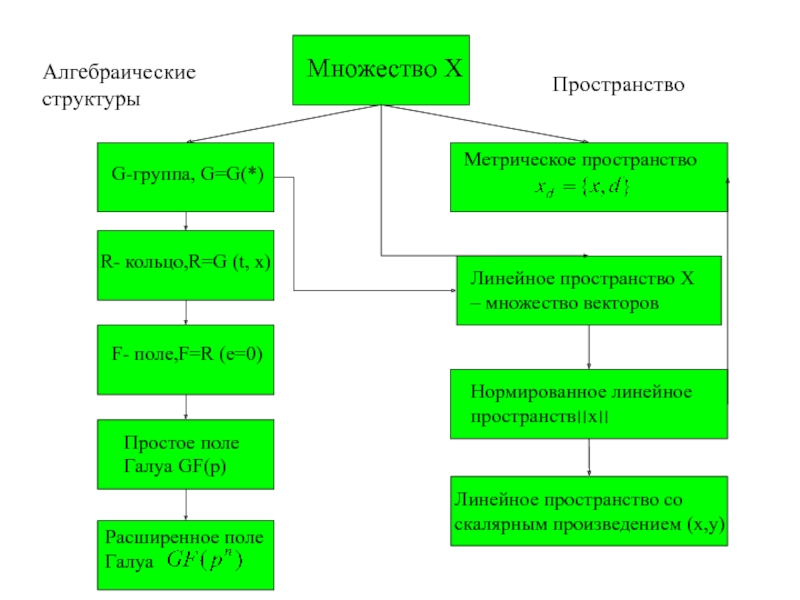
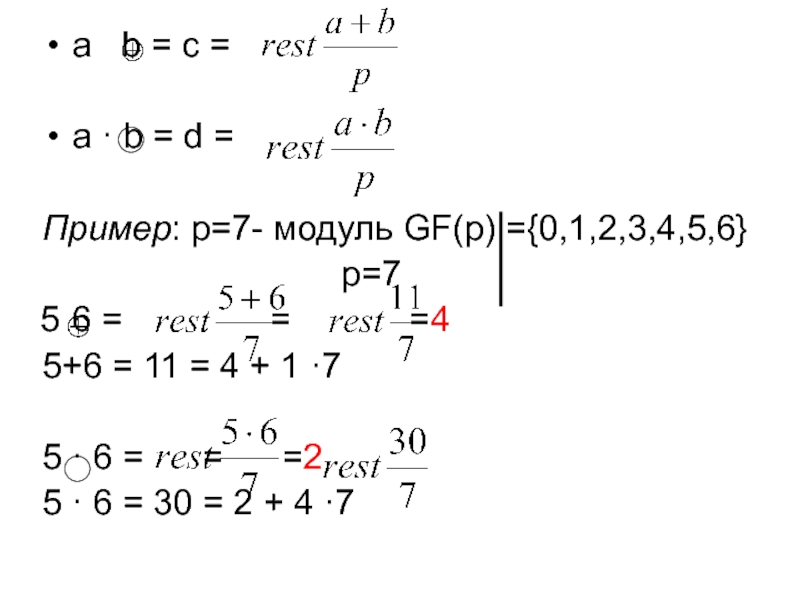Галуа GF(p)
Расширенное поле Галуа
Метрическое пространство
Линейное пространство X –
множество векторовНормированное линейное пространств׀׀x׀׀
Линейное пространство со скалярным произведением (x,y)