МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

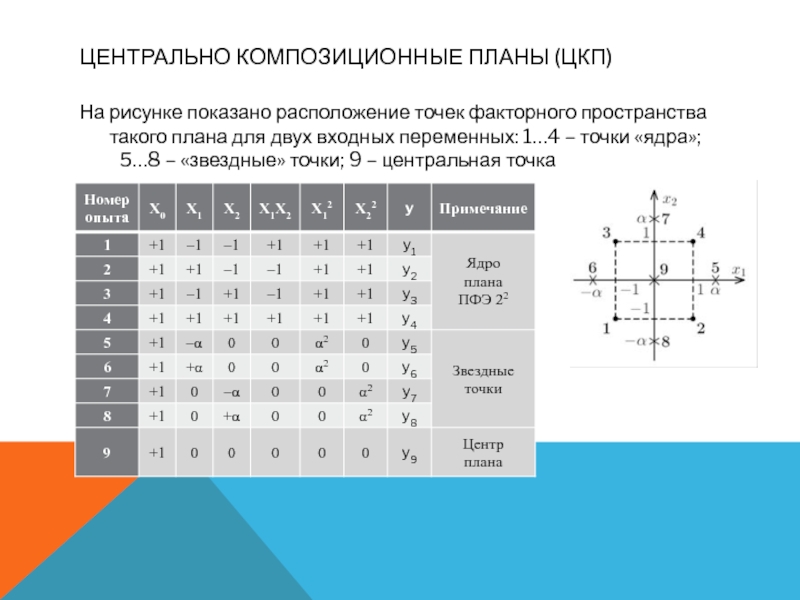
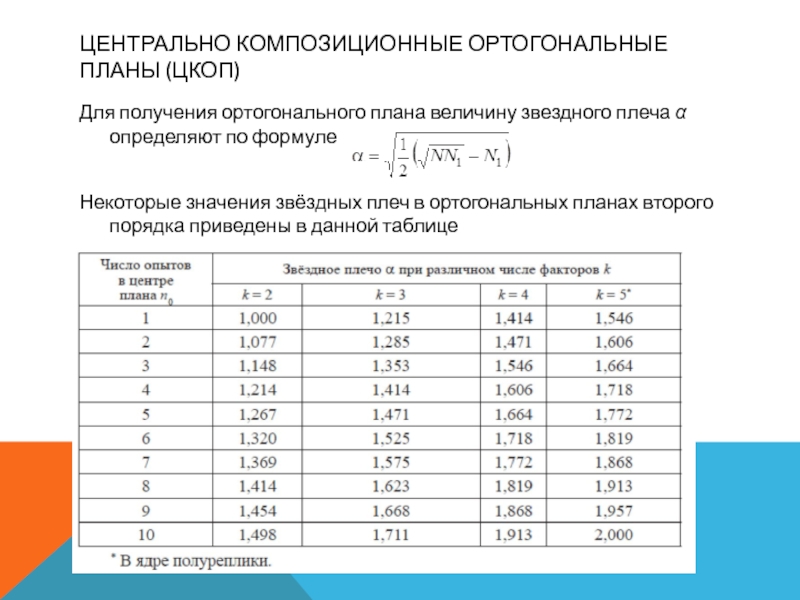
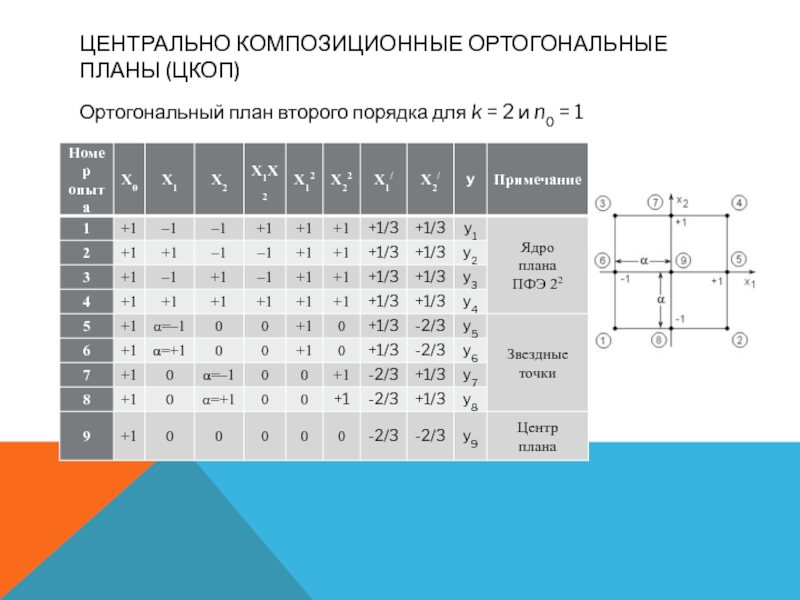
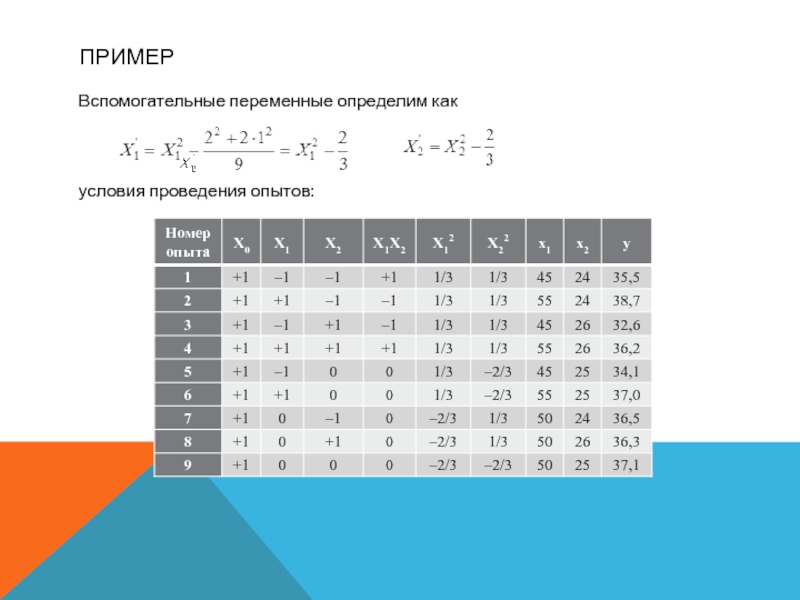
удается, то переходят к планам второго порядка.
Для получения коэффициентов

регрессии в этом случае варьирования факторами на двух уровнях недостаточно (в случае одного фактора для построения прямой необходимо две точки, для построения параболы – три точки). При небольшом количестве факторов можно варьировать каждый фактор на трех уровнях – верхнем, нижнем и нулевом. Полнофакторный эксперимент в таком случае обозначается как 3k.
Этот эксперимент содержит 9 опытов. Уравнение, для получения которого он предназначен, имеет 6 членов и записывается как

.

N=3k опытов. С ростом числа факторов количество опытов резко возрастает.

Так при k=3 их 27, а число коэффициентов b — 10, при k=5 число опытов 243, а коэффициентов 21.
В связи с этим осуществить ПФЭ для планов второго порядка не только сложно, но и нецелесообразно.

композиционным или последовательным планом, разработанным Боксом и Уилсоном.
Они обосновали возможность

использования схем, в которых план типа ПФЭ 2k (при k<5) или ДФЭ 2k-1 (при k5) используемый в качестве «ядра», дополняется 2k «звездными» точками (по две на каждый фактор), и n0 опытами в центре плана (если ранее проведены параллельные опыты, n0 можно принять равным 1).
Расстояние от центра плана до звездной точки называется звездным плечом.
Общее количество опытов с использованием звездных точек составляет

где – число опытов в ядре плана

такого плана для двух входных переменных: 1…4 – точки «ядра»;

5…8 – «звездные» точки; 9 – центральная точка

плеча α определяют по формуле

Некоторые значения звёздных плеч в ортогональных

планах второго порядка приведены в данной таблице

= 2 и n0 = 1

коэффициенты уравнения регрессии c определяются независимо один от другого по

формулам.

продукта реакции у (%) зависит от температуры реакционной смеси x1

(°С) и концентрации реагента х2 (%) при x01= 50 °С, Δx1= 5 °С; x02= 25 %, Δx2= 1 %.
Решение. Связь между кодированными и натуральными величинами определяется по


Рассчитаем коэффициенты вспомогательного уравнения

Имеем k = 2 фактора. Число опытов в центре плана n0=1. Общее число опытов.

Величина звездного плеча α = 1.

Н.А. Спирин, В.В. Лавров, В.Ю. Рыболовлев, Л.Ю. Гилева, А.В. Краснобаев,

В.С. Швыдкий, О.П. Онорин, К.А. Щипанов, А.А. Бурыкин; под ред. Н.А. Спирина. – Екатеринбург: ООО «УИПЦ», 2014. – 558 с.