Слайд 1МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ОБЪЕКТОВ ТУРИСТИЧЕСКОЙ ИНДУСТРИИ
С ИСПОЛЬЗОВАНИЕМ ТЕОРИИ ГРАФОВ
С.А. Гуцанович
Слайд 2ЦЕЛИ ЛЕКЦИИ:
во-первых, обобщить и систематизировать знания по элементам теории
графов, полученные на предыдущих занятиях курса и дисциплины «Высшая математика»;
во-вторых, сформировать умения и способы деятельности, связанные с новыми понятиями и свойствами теории графов, направленные на изучение и построение более сложных систем посредством методов математического моделирования в индустрии туризма;
в-третьих, выработать определенные потребности и желания в моделировании и описании деятельности туристической отрасли с использованием теории графов.
Слайд 3ПЛАН ЛЕКЦИИ:
1. Пропедевтика теории графов при осуществлении математического моделирования.
2. Элементы
теории графов на элементарных практических примерах.
3. Проблемная область математического моделирования
с использованием теории графов.
4. Базовые понятия теории графов, их классификации и интерпретации в сфере туризма и гостеприимства.
5. Некоторые свойства графов и их использование в индустрии туризма.
6. Туристические объекты и установление отношений между ними с помощью двудольных графов.
7. Прикладные направления теории графов при моделировании объектов и отношений в туристической отрасли.
8. Примерная тематика рефератов и литературы по теории графов.
Слайд 4РАЗДЕЛ I. ТЕОРЕТИЧЕСКИЕ И ПРИКЛАДНЫЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
В СФЕРЕ ТУРИЗМА
И ГОСТЕПРИИМСТВА
Тема 1.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ИХ ЗНАЧЕНИЕ
В ТУРИСТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ
Тема
1.2. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
ПРИ МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ
РЕАЛЬНЫХ ПРОЦЕССОВ И ОБЪЕКТОВ
Тема 1.3. ИСПОЛЬЗОВАНИЕ СРЕДСТВ МАТЕМАТИКИ
В ПРОЦЕССЕ МОДЕЛИРОВАНИЯ ПРОЕКТОВ
В СФЕРЕ ТУРИСТИЧЕСКИХ УСЛУГ
Слайд 5Моделью называется искусственный объект, который описывает строение и основные свойства
реального объекта или реальной ситуации с целью изучения последних. Процесс
построения моделей называется моделированием.
Модели бывают различных видов, например: физическими, когда моделью служит физическое тело; знаковыми, в которых объекты, явления или ситуации описываются с помощью определенных символов (знаков).
Слайд 6 Под моделью понимается вспомогательный объект, находящийся в определенном соответствии
с изучаемым объектом-оригиналом и более удобный для решения задач конкретного
исследования.
Отражая отдельные особенности поведения объекта-оригинала, модель имеет некоторые идентичные черты с оригиналом и служит для получения такой информации о нем, которую затруднительно либо невозможно получить путем непосредственного исследования оригинала.
Слайд 7Этапы построения моделей
формализация (переход от реальной ситуации к построению модели);
нахождение
взаимосвязей между ее компонентами;
разрешение проблемы внутри модели (исследование);
интерпретация результата при
переходе к реальной ситуации.
Слайд 8 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ –
1) класс неопределяемых (абстрактных, символических)
математических объектов (таких как числа и векторы и др.) и
математические отношения между ними;
2) замена реального процесса математическими отношениями так, чтобы изучаемые стороны процесса не претерпели существенного искажения;
3) в математической теории эксперимента – связь параметра (критерия) оптимизации с факторами.
Слайд 9Среди знаковых можно выделить математические модели, в которых описание объектов
или ситуаций происходит с помощью математических средств.
Переход от задачи, условие
которой задано словами, к математическим уравнениям или неравенствам – это простейший пример математического моделирования. При таком моделировании Вам не приходилось изучать ситуацию: Вам ее предлагали уже изученной в виде условия задачи. Однако Вы определяли неизвестные переменные, составляли уравнения, неравенства или их системы, которые связывали неизвестные величины с известными, затем находили значения неизвестных или их комбинаций и отбирали неизвестные, подходящие по смыслу задачи. Первые два этапа Ваших действий можно отнести к построению модели, два следующих – к ее исследованию.
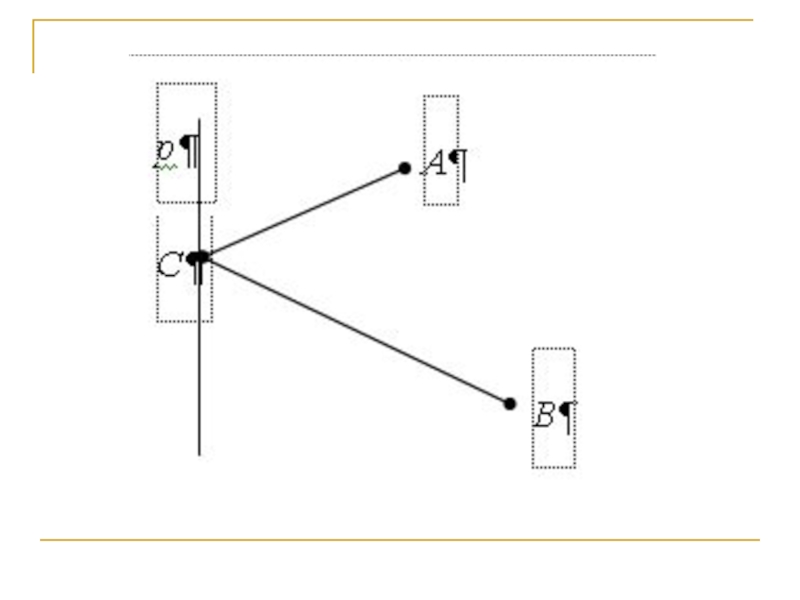
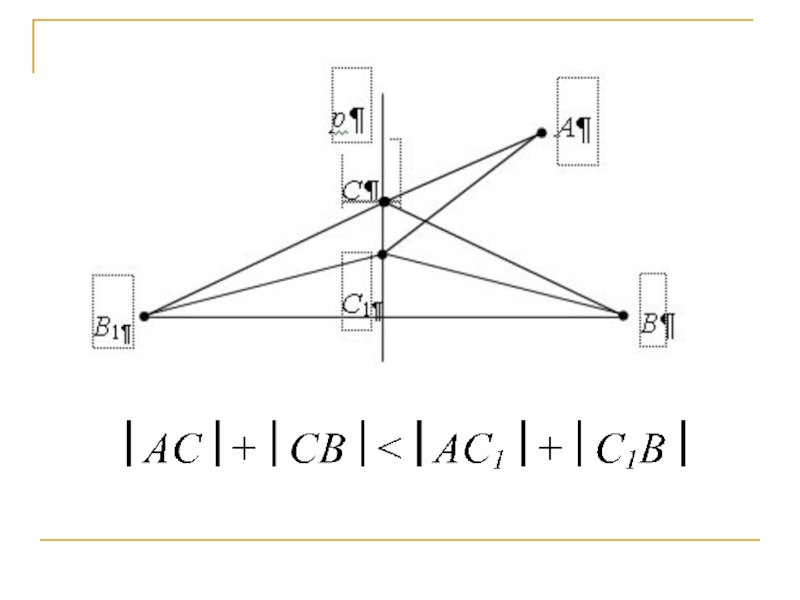
Слайд 19«Золотое» сечение
в архитектурных сооружениях
Древнегреческий Парфенон состоит из 8 колонн по
коротким сторонам и 17 по длинным. Отношение высоты здания к
его длине примерно равно 0,618, то есть равняется коэффициенту «золотого сечения».
Слайд 20Теоретическая модель определяет некоторую фиксированную связь элементов, предполагает определенную структуру,
имеющую внутренние, существенные отражения реальности объектов туристической индустрии в идеализированном
виде.
Нормативная модель воплощает в себя совокупность отдельных систем и элементов с их взаимосвязями и соответствующим содержательным описанием, позволяющим значительно повысить эффективность деятельности в сфере туризма.
Слайд 21Величины, характеризующие функционирование системы индустрии туризма (рис.), разделим на три
категории:
внешние воздействия u1, u2,..., uk влияющие на поведение системы
выходные переменные
y1, y2, …, ym, описывающие те аспекты поведения системы, которые представляют интерес для исследования;
переменные, характеризующие состояние системы х1, х2,..., хn.
Рис. Модель взаимодействия системы индустрии туризма с окружающей средой
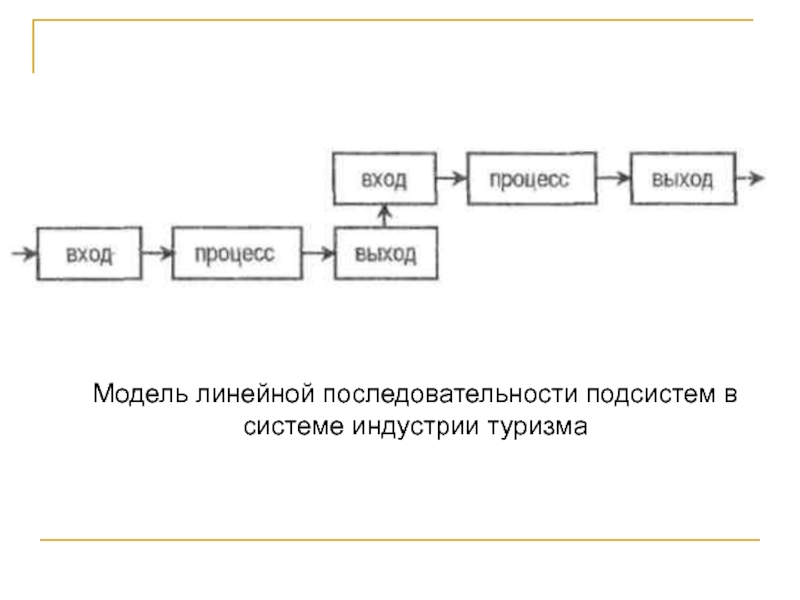
Слайд 22Модель линейной последовательности подсистем в системе индустрии туризма
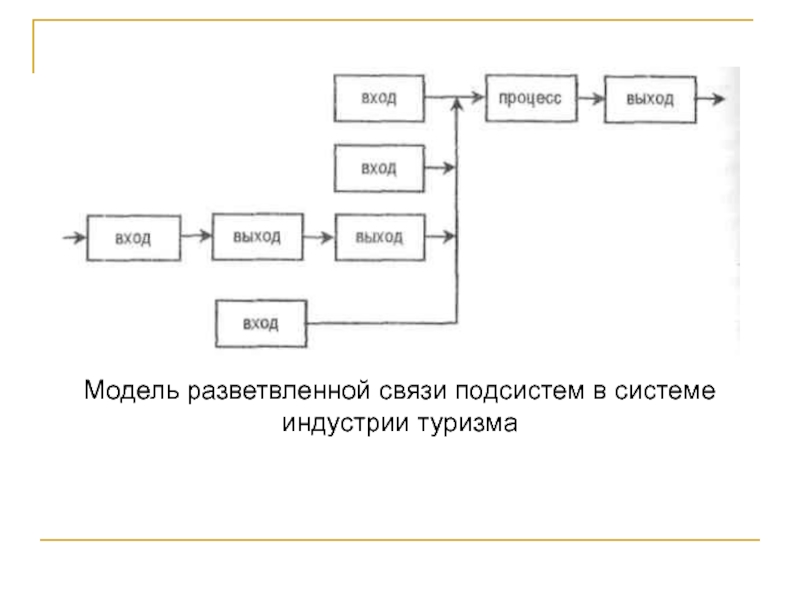
Слайд 23Модель разветвленной связи подсистем в системе индустрии туризма
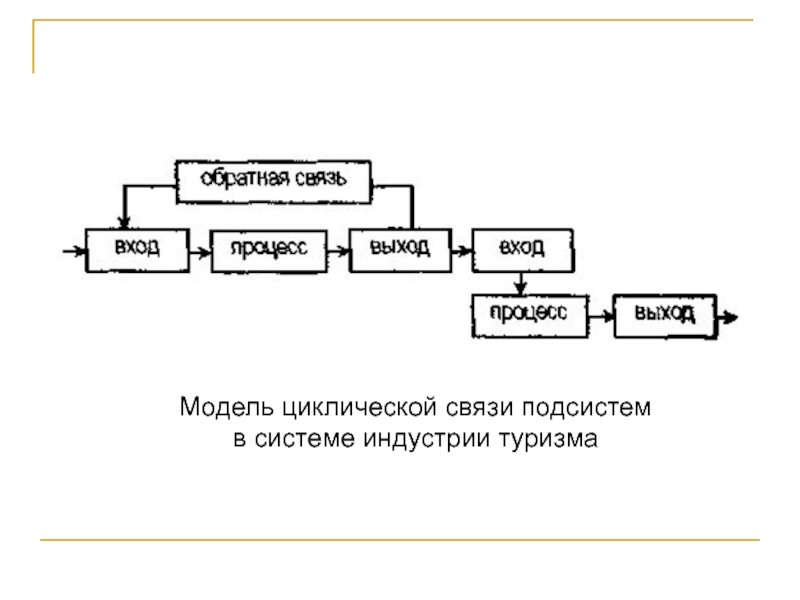
Слайд 24Модель циклической связи подсистем
в системе индустрии туризма
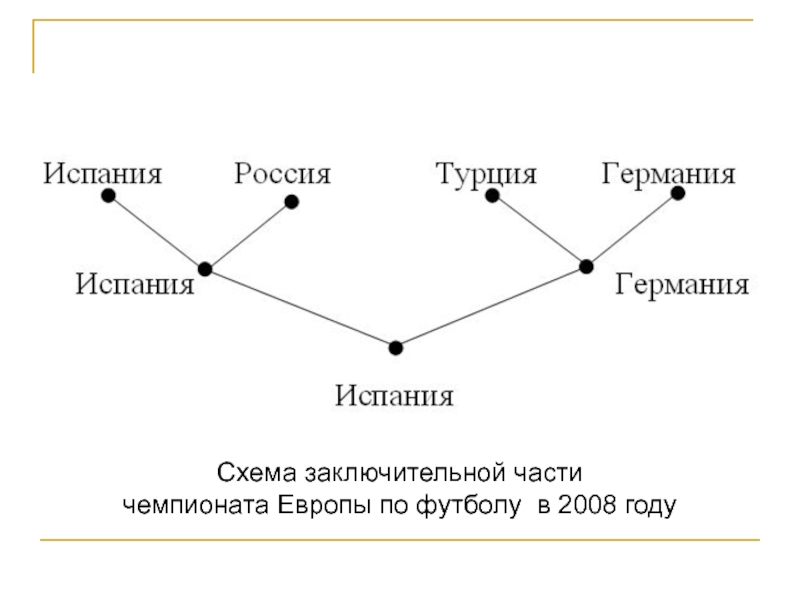
Слайд 27Схема заключительной части
чемпионата Европы по футболу в 2008 году
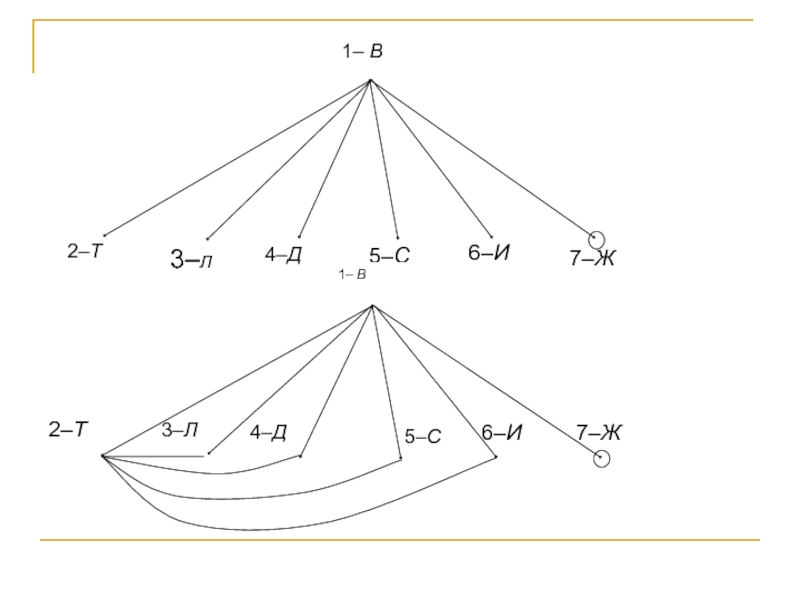
Слайд 28Пример
В шахматном турнире, в котором каждый участник должен сыграть с
каждым, зарегистрировались семь участников туристического пансионата. Известно, что к настоящему
времени В сыграл шесть партий, Т – пять, Л и Д – по три, С и И – по две, Ж – одну. С кем сыграл Л?
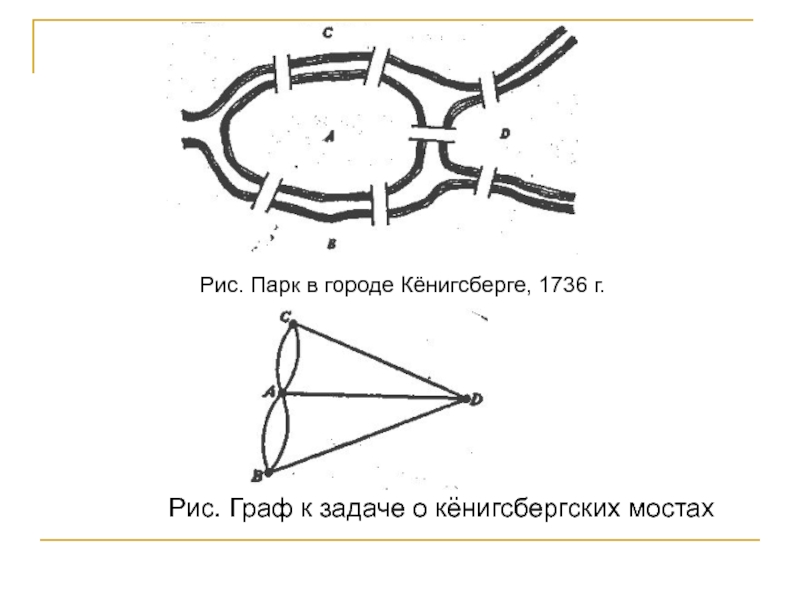
Слайд 30Начало теории графов можно отнести к 1736 году, когда Л.
Эйлер решил популярную в то время задачу о кенигсбергских мостах.
Этот результат более ста лет был единственным результатом в теории графов.
В XX в. теория графов превратилась в один из наиболее бурно развивающихся разделов математики.
С помощью графов можно изображать различные объекты, схемы железных и шоссейных дорог, нефтепроводов и газопроводов, электрические и электронные схемы, химические молекулы, результаты спортивных турниров, отношения между людьми, туристические маршруты
Проблемные ситуации, которые решаются посредством математического моделирования с использованием теории графов возникают в различных науках и сферах жизнедеятельности, включая индустрию туризма.
Для универсального введения понятия графа используется язык теории множеств.
Слайд 31Рис. Парк в городе Кёнигсберге, 1736 г.
Рис. Граф к задаче о
кёнигсбергских мостах
Слайд 32Задача о коммивояжере (посыльном)
Имеется k городов, расстояния между которыми известны;
коммивояжер отправляется в путь из одного из них с тем,
чтобы посетить все остальные (k-1) города ровно по одному разу каждый и вернуться в исходный город.
Уже была рассмотрена одна задача о пути на графе, в ней требовалось обойти граф, так, чтобы путь пролегал по каждому ребру только один раз. Такие маршруты на графе называют эйлеровыми. В новой задаче требуется найти такой путь на РАФе, чтобы любая его вершина была пройдена только один раз. Такие пути на графе называют гамильтоновыми в честь ирландского математика У. Гамильтона.
Слайд 33Визуальный вид построения модели можно осуществить в виде блок-схемы (графа),
где точками обозначаются элементы объекта, линиями функции отдельных элементов, а
также связи между элементами и другие логические переходы. В последствие точки могут быть преобразованы в различные геометрические фигуры, с соответствующими надписями, что будет показано ниже.
В отдельных случаях, чтобы подчеркнуть степень связи, вместо линий, точки соединяют направленными линиями со стрелками.
Для выделения различий объектов точки могут быть представлены несколькими цветами или выглядеть по-разному.
Первоначальные представления определенной структуры в виде графа могут впоследствии продолжаться более разнообразным чертежным описанием как самих точек, так и линий.
Слайд 34Обычно графы обозначаются большими латинскими буквами G, H, F. Вершины
графа обозначаются малыми латинскими буквами или цифрами. Ребро, соединяющее вершины
u и v обозначается. (u, v). Если две вершины соединены ребром, то они называются смежными.
Число ребер, выходящих из вершины u, называется степенью этой вершины и обозначается deg(u) или d(u), а в упрощенном виде G(u).
Мы будем рассматривать графы, ребра которого имеют направление. Такие графы имеют специальное название ориентированные графы.
Ориентированным графом (или орграфом) называется конечное множество точек, расположенных на плоскости (листе бумаги), некоторые пары из которых соединены линией, имеющей направление от одной точки к другой. При этом точки называются вершинами ориентированного графа, а линии – дугами или ориентированными ребрами ориентированного графа
Слайд 35Граф состоит из точек, изображенных на плоскости, и линий, соединяющих
некоторые пары точек. Точки называются вершинами графа, а линии –
его ребрами. Число ребер, выходящих из вершины, называется степенью вершины. Две вершины, соединенные ребром, называются смежными.
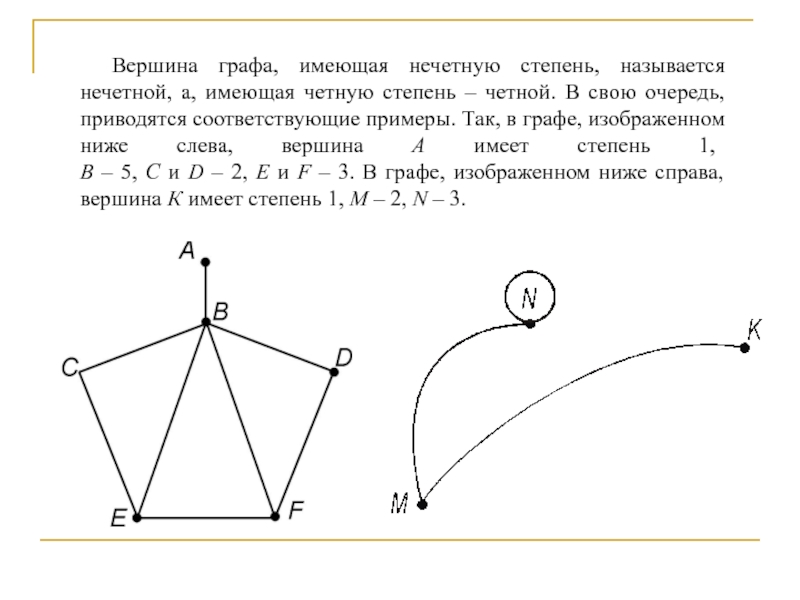
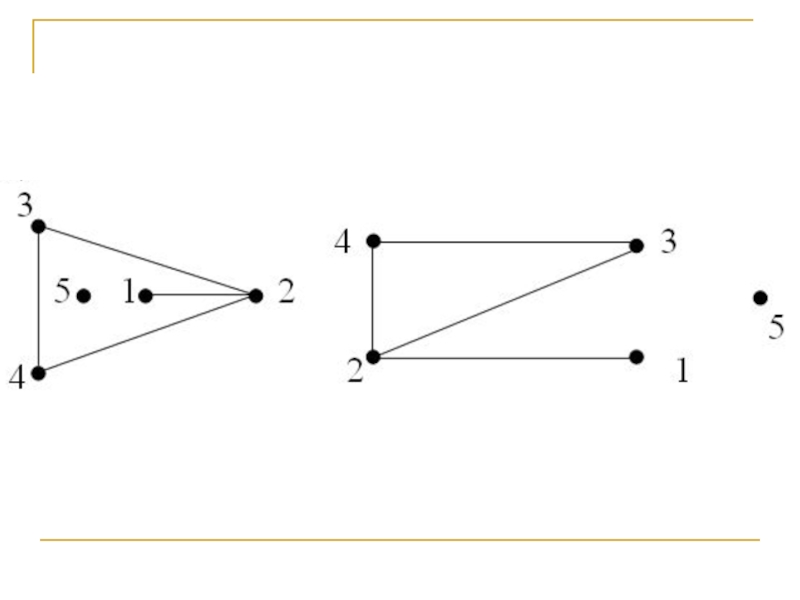
Слайд 36Вершина графа, имеющая нечетную степень, называется нечетной, а, имеющая четную
степень – четной. В свою очередь, приводятся соответствующие примеры. Так,
в графе, изображенном ниже слева, вершина А имеет степень 1,
В – 5, С и D – 2, E и F – 3. В графе, изображенном ниже справа, вершина К имеет степень 1, М – 2, N – 3.
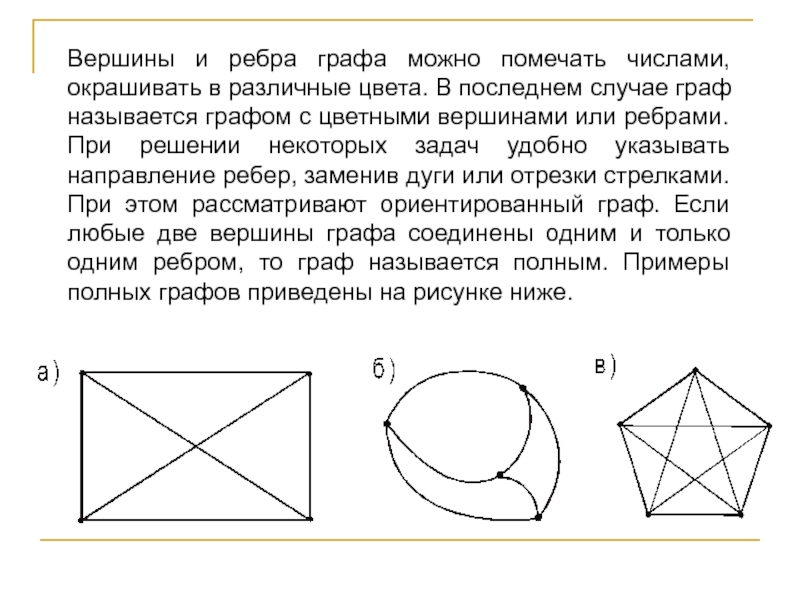
Слайд 37Вершины и ребра графа можно помечать числами, окрашивать в различные
цвета. В последнем случае граф называется графом с цветными вершинами
или ребрами. При решении некоторых задач удобно указывать направление ребер, заменив дуги или отрезки стрелками. При этом рассматривают ориентированный граф. Если любые две вершины графа соединены одним и только одним ребром, то граф называется полным. Примеры полных графов приведены на рисунке ниже.
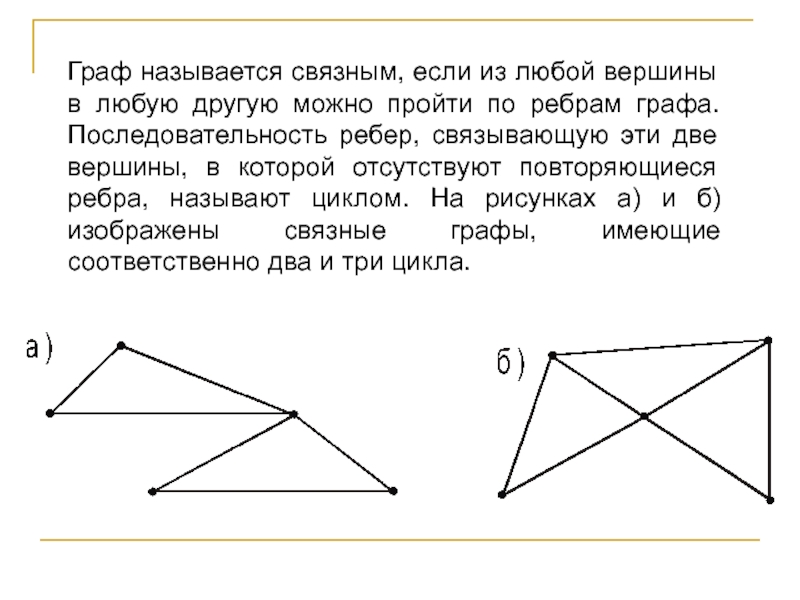
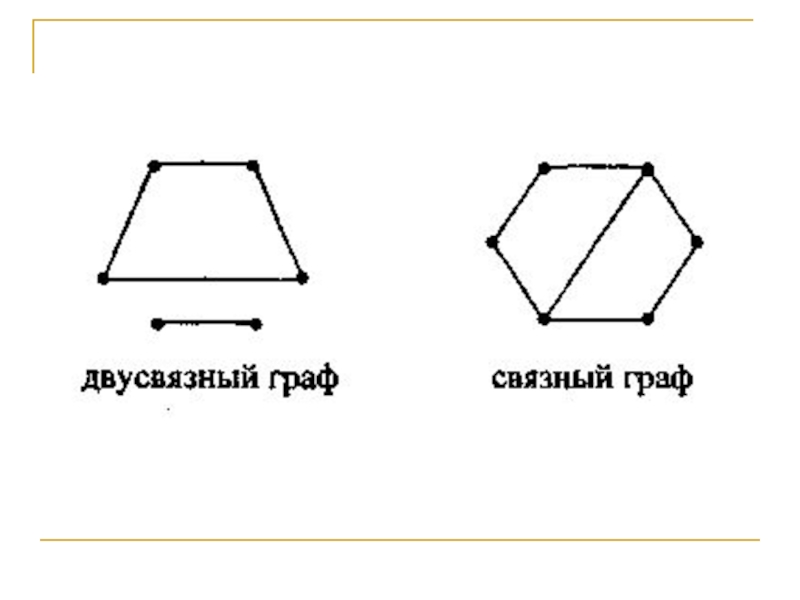
Слайд 38Граф называется связным, если из любой вершины в любую другую
можно пройти по ребрам графа. Последовательность ребер, связывающую эти две
вершины, в которой отсутствуют повторяющиеся ребра, называют циклом. На рисунках а) и б) изображены связные графы, имеющие соответственно два и три цикла.
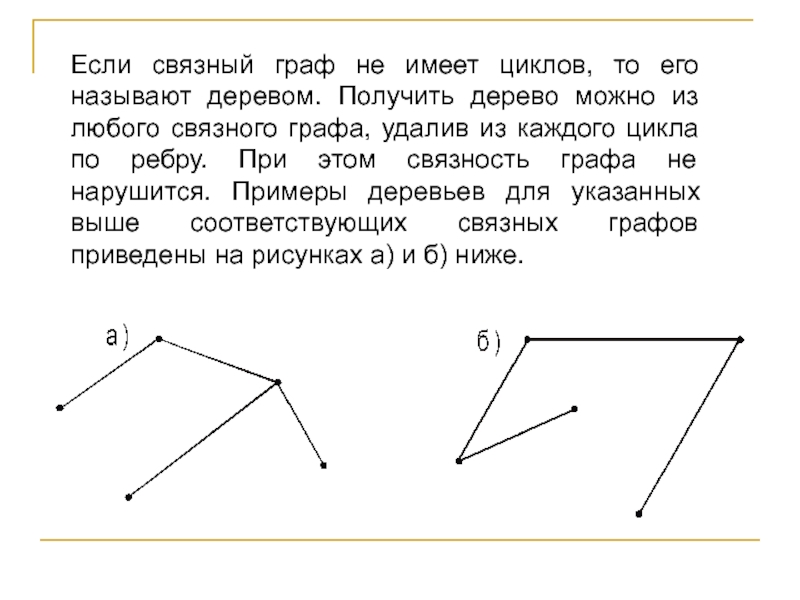
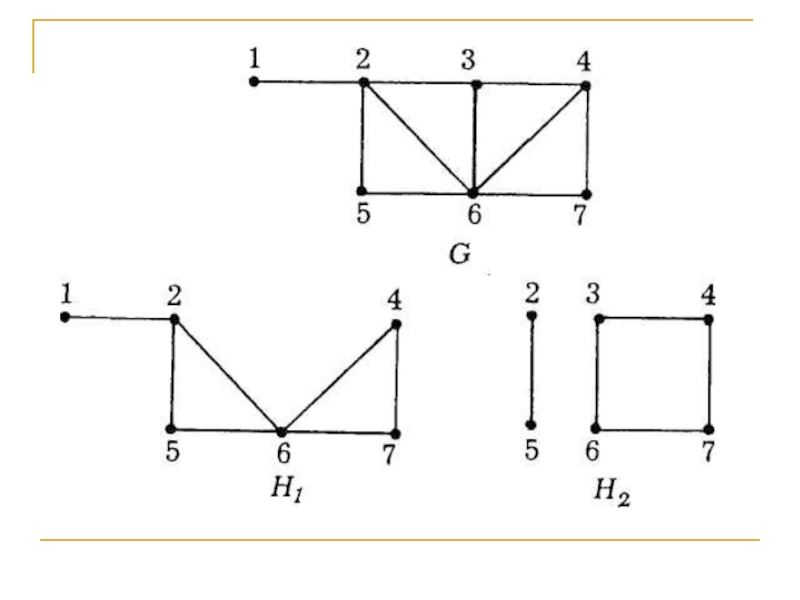
Слайд 39Если связный граф не имеет циклов, то его называют деревом.
Получить дерево можно из любого связного графа, удалив из каждого
цикла по ребру. При этом связность графа не нарушится. Примеры деревьев для указанных выше соответствующих связных графов приведены на рисунках а) и б) ниже.
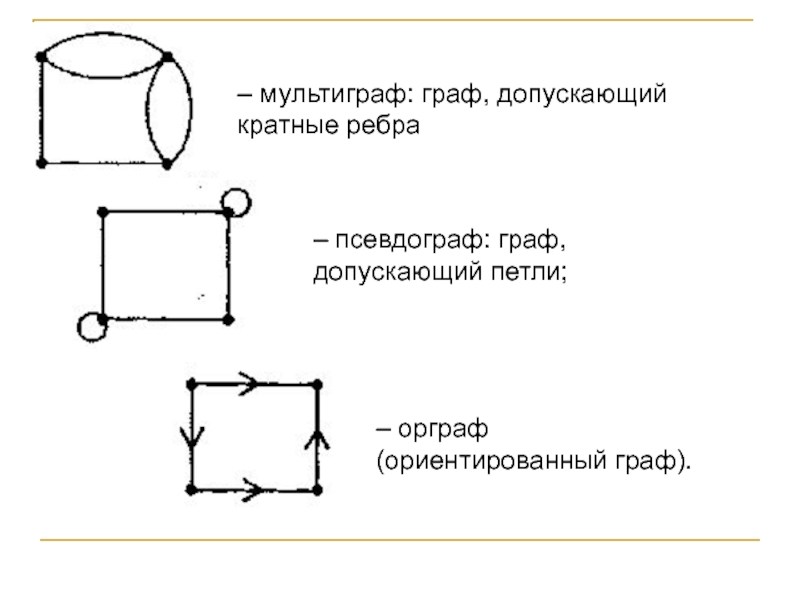
Слайд 40– мультиграф: граф, допускающий кратные ребра
– псевдограф: граф, допускающий петли;
–
орграф
(ориентированный граф).
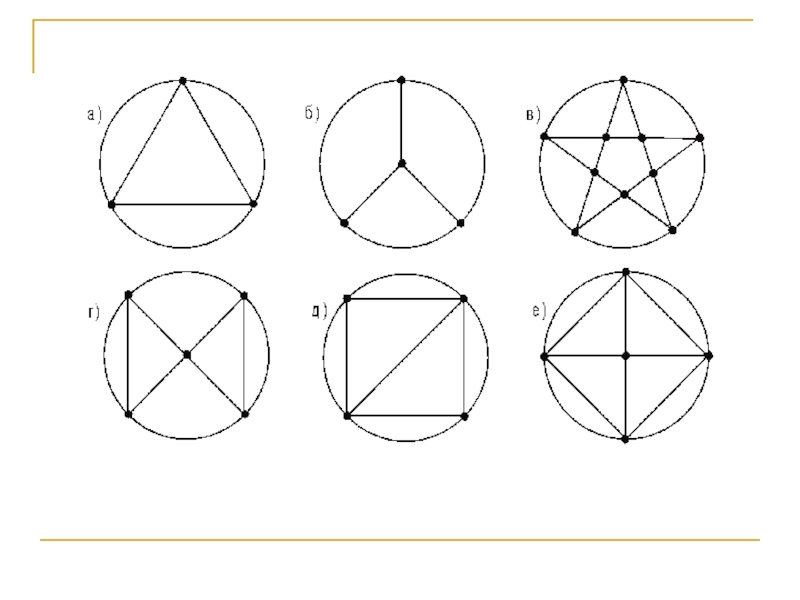
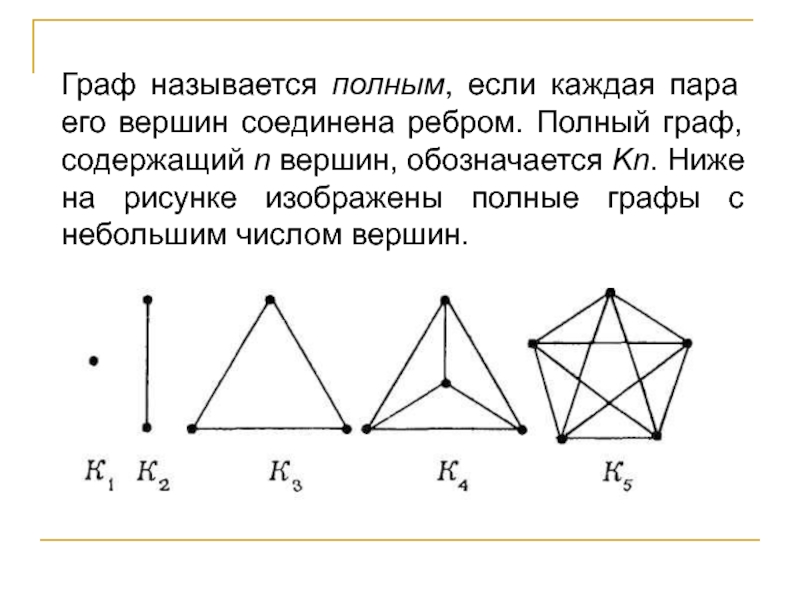
Слайд 43Граф называется полным, если каждая пара его вершин соединена ребром.
Полный граф, содержащий n вершин, обозначается Kn. Ниже на рисунке
изображены полные графы с небольшим числом вершин.
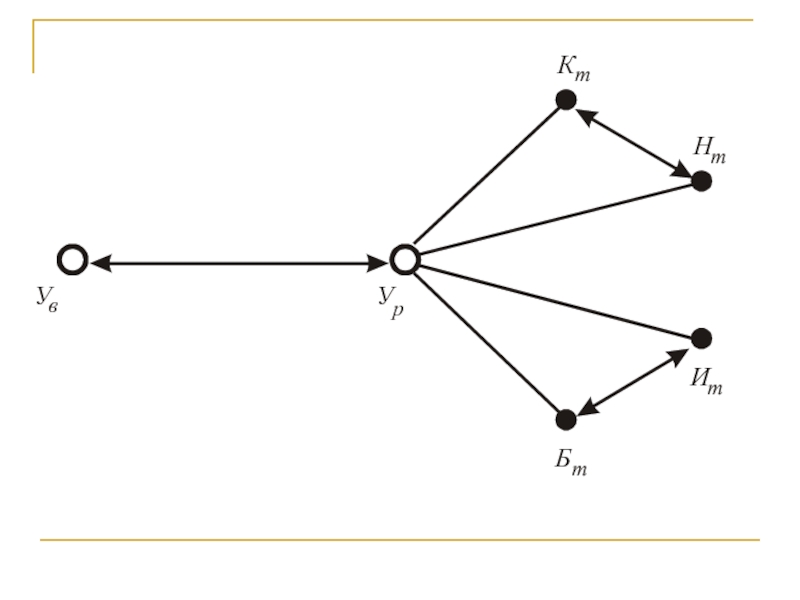
Слайд 46Из рисунка видно, что в туристическом пансионате разработана специальная программа
обучения различным видам танца, которая осуществляется на основе взаимодействия обучающего
(Ув) и обучающихся (Уд).
В свою очередь, рекомендуется проведение занятий по формированию умений владеть четырьмя видами танца по принципу: соединение на одном занятии классического (Кт) и народно-сценического (Нт),
а на другом – историко-бытового (Ит) и бальных (Бт) танцев.
Слайд 47В шахматном турнире пансионата, в котором каждый участник встречался с
каждым, один шахматист заболел и не доиграл свои партии. Всего
в турнире было проведено 23 встречи. Сколько шахматистов участвовали в турнире? Сколько партий сыграл выбывший участник?
В оздоровительном комплексе окончилось соревнование по настольному теннису, в котором каждый игрок встретился с каждым. Было проведено 45 встреч. Определите число игроков.
В двух теннисных командах одинаковое число игроков. Каждый игрок одной команды встретился с каждым игроком второй команды. Сколько встреч проведено, если в командах: а) по 3 игрока; б) по 4 игрока; в) по 5 игроков?
В двух теннисных командах одинаковое число игроков. Каждый игрок одной команды встретился с каждым игроком второй команды. Сколько игроков в командах, если проведено: а) 16 встреч; б) 25 встреч; в) 49 встреч; г) 81 встреча?
Слайд 49Свойство.
Сумма степеней вершин графа есть число четное.
Свойство следует из
особенностей самих отрезков: какой бы отрезок мы ни взяли, он
имеет две вершины. Поэтому число вершин в любом количестве отдельно взятых отрезков четно.
Примеры.
В гостиничном ресторане за столом сидят четверо туристов. Может ли быть ситуация, что трое туристов знакомы с тремя, а один с двумя? Какие могут быть другие ситуации.
В спортивно-оздоровительном комплексе проводится турнир по теннису, в котором участвует 5 игроков. Может ли случиться такая ситуация, при которой трое из них проведут по 3 встречи, а двое по две.
Слайд 50Граф называется двудольным, если существует такое разбиение множества его вершин
на две части (доли), что концы каждого ребра принадлежат разным
частям.
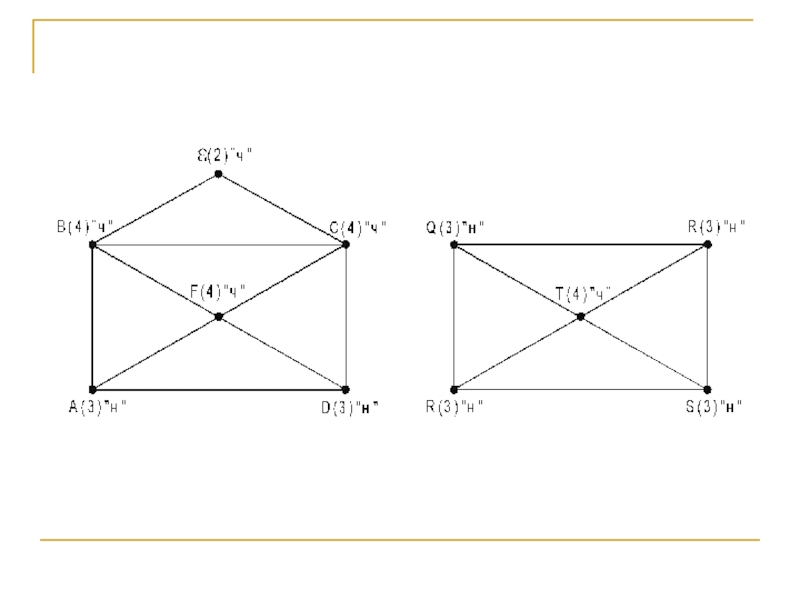
На рисунке изображены два различных двудольных графа (Вершины одной доли помечены I, второй – II.)
Слайд 51Свойство. Суммы степеней вершин двудольного графа равны.
Пусть v1, v2,…, vk
– вершины одной доли, а u1, u2, …, up –
вершины другой доли. Тогда из одной доли выходит d(v1) + d(v2) + … + d(vk) ребер, а из другой – d(u1) +d(u2) +… + d(up) ребер. Равенство сумм следует из того, что это одни и те же ребра.
Слайд 52Пример. На туристическом слете в Минске туристов России и Беларуси
каждый россиянин знаком ровно с пятью белорусами, а каждый белорус
– ровно с четырьмя россиянами. В гостинице забронировано 16 двуместных номеров, а на последней экскурсии по Минску было 23 туриста. Сколько туристов было на туристическом слете в Минске?
Слайд 53Решение. Поставим в соответствие туристам вершины графа, а если два
туриста дружат, то соединим ребром соответствующие им вершины. Поскольку мы
учитываем лишь дружбу россиян и белорусов, то граф будет двудольным.
Пусть россиянам соответствует доля А, в которой m вершин, а белорусам доля В, в которой n вершин. Из вершин доли А выходит 5m ребер, а из вершин доли В – 4n ребер. По свойству 5m = 4n и n = 5/4m. Согласно условия, 23 ≤ m + n ≤ 32. Решив последнее неравенство и учитывая условие целочисленности, получаем 11 ≤ m ≤ 14. Поскольку m должно делиться на 4, то m = 12. Отсюда и n = 15. Всего на туристическом слете в Минске 27 туристов.
Слайд 54Прикладные направления теории графов при моделировании объектов и отношений в
туристической отрасли.
1. Задачи обеспечения или задачи о размещении. Например, «транспортные»
задачи, в которых вершинами графа являются пункты, а ребрами – транспортные маршруты. Другой пример – сети снабжения, в которых вершинами являются пункты производства и потребления, а ребрами – возможные маршруты перемещения.
2. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных и финансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями.
Слайд 55Прикладные направления теории графов при моделировании объектов и отношений в
туристической отрасли.
3. Управление проектами. Например, проект строительства некоторого объекта. Решаются
задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).
4. Модели коллективов и групп основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства, доверия, симпатии и т.д.) – в виде ребер или дуг. Решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности взаимодействия, и др.
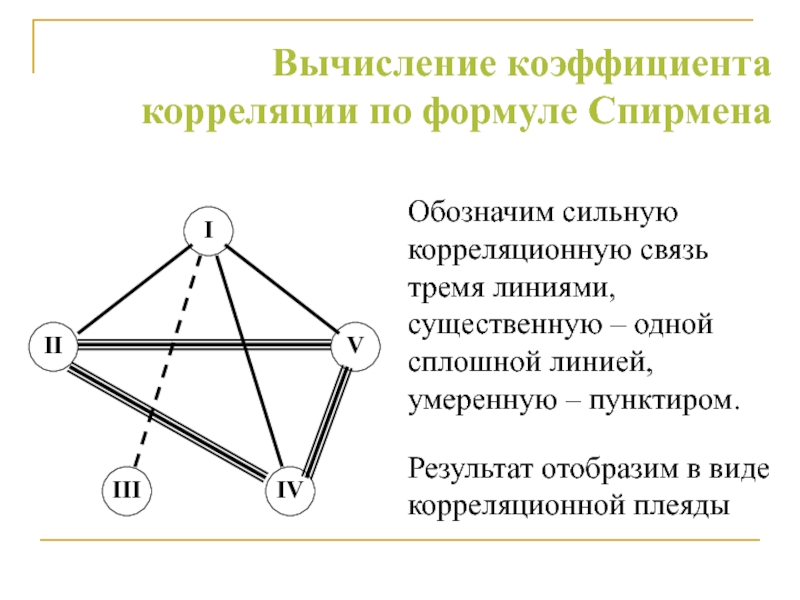
Слайд 56Вычисление коэффициента корреляции по формуле Спирмена
Обозначим сильную корреляционную связь тремя
линиями, существенную – одной сплошной линией, умеренную – пунктиром.
Результат отобразим
в виде корреляционной плеяды
Слайд 58ПРИМЕРНАЯ ТЕМАТИКА РЕФЕРАТОВ
Математическое моделирование системы спортивно-туристической деятельности в условиях региона
с использованием теории графов.
Графовые модели туристических маршрутов областного города с
районными центрами.
Использование свойств теории графов для построения рациональной структуры функционирования туристического комплекса.
Построение математических моделей систем живой и неживой природы с использованием свойств теории графов для повышения менеджмента качества в туризме.
Различные виды двудольных графов при моделировании ситуаций взаимодействия в студенческой среде.
Построение различных типов графов при участии в экологических экспедициях.
Слайд 59ОСНОВНАЯ ЛИТЕРАТУРА
2. Бурков, В.Н. Теория графов в управлении организационными системами
/ В.Н Бурков, А.Ю. Заложнев, Д.А. Новиков. – М.: Синтег,
2001. – 115 с.
5. Гуцанович, С.А. Элементы дискретной математики в занимательных примерах и задачах: научно-популярное издание для молодежи / О.И.. Мельников.– Минск: НИО, 2008. – 80 с.
6. Емеличев, В.А. Лекции по теории графов /В.А. Емеличев, О.И. Мельников, В.И. Сарванов, Р.И. Тышкевич. – М.: Наука, 1990. –382 с.
10. Мельников, О.И. Занимательные задачи по теории графов / О.И. Мельников. – Минск: НТООО «ТетраСистемс», 2001. – 144 с.
11. Мельников, О.И. Математическое моделирование в системе Марlе / О.И. Мельников, А.А. Морозов. – Минск: Нац. ин-т образования, 2009. – 88 с.
14. Оре, О. Графы и их применение / О. Оре. – М.: URSS, 2008. – 170 с.
17. Харари, Ф. Теория графов / Ф. Харари. – М.: Едиториал УРСС, 2003. – 300 с.
Слайд 60ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
7. Евстигнеев, В.А. Теория графов: алгоритмы обработки деревьев /
Отв. ред. В.Е. Котов. – Новосибирск.: ВО «Наука», 1994. –
360 с.
12. Костюкова, Н.И. Графы и их применение. Комбинаторные алгоритмы для программистов / Н.И. Костюкова. – М.: Интернет-университет информационных технологий, 2007. – 310 с.
13. Мельников, О.И. Незнайка в стране графов / О.И. Мельников. – Минск, «Оракул». 1998. – 256 с.
16. Мудров, В.И. Задача о коммивояжере / В.И. Мудров. – М.: Знание, 1969. – 62 с.