МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЗАДАЧАХ АДДИТИВНЫХ ТЕХНОЛОГИЙ

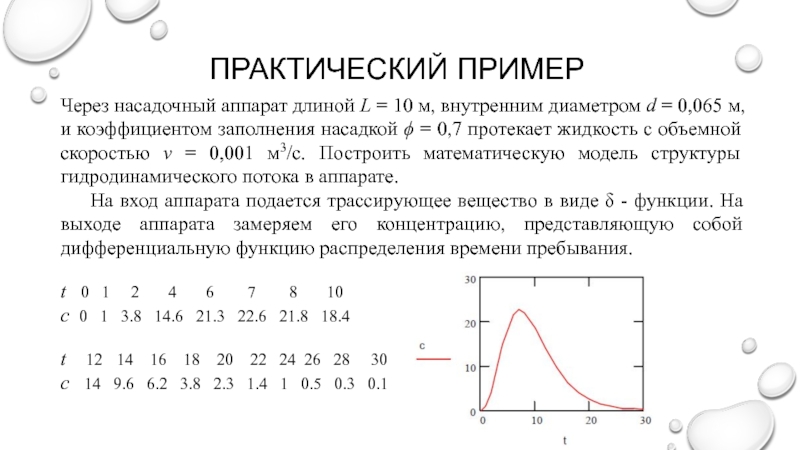
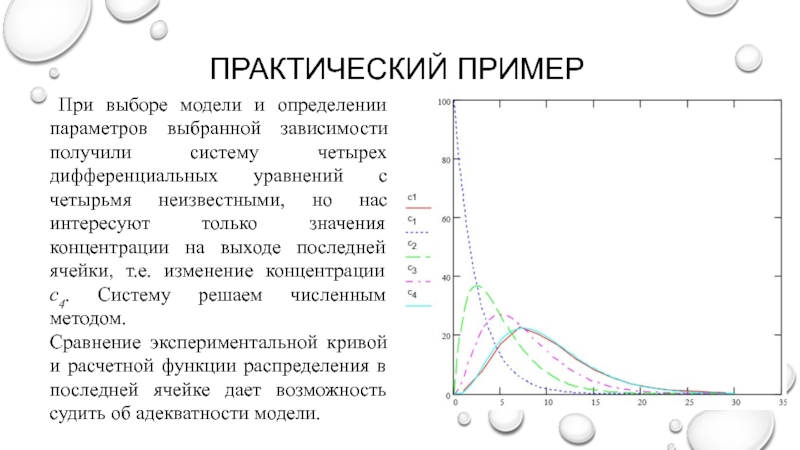
функций отклика. Используется понятие момента, согласно которому, функция распределения случайной

величины может быть охарактеризована числовыми величинами (моментами различных порядков).
Безразмерным начальным моментом i - го порядка, характеризующим  - кривую, является интеграл вида:


где t и (t) – безразмерные время и концентрация.
Безразмерный центральный момент i - го порядка имеет вид:

вводе трассера в поток на входе его в аппарат, первый

начальный момент М1 представляет собой среднее время пребывания.
Первый центральный момент всегда равен нулю, т.е. 1 = 0.
Второй центральный момент, называемый дисперсией, является мерой рассеяния времени пребывания и определяется по формуле


Третий центральный момент 3 называется асимметрией, характеризует степень асимметричности кривой распределения ( - кривой), и определяется из уравнения

распределения и равен


Обычно при расчете моментов по экспериментальным кривым используется

ступенчатая аппроксимация, т.е. расчет моментов выполняется по формулам:
– начальные моменты


– масштабированные моменты

соотношения
Алгоритм идентификации математической модели структуры потока - это вычисление всех

моментов и определение с их помощью параметров модели.

 

диаметром d = 0,065 м, и коэффициентом заполнения насадкой 

= 0,7 протекает жидкость с объемной скоростью v = 0,001 м3/с. Построить математическую модель структуры гидродинамического потока в аппарате.
На вход аппарата подается трассирующее вещество в виде  - функции. На выходе аппарата замеряем его концентрацию, представляющую собой дифференциальную функцию распределения времени пребывания.

t 0 1 2 4 6 7 8 10
c 0 1 3.8 14.6 21.3 22.6 21.8 18.4

t 12 14 16 18 20 22 24 26 28 30
c 14 9.6 6.2 3.8 2.3 1.4 1 0.5 0.3 0.1

можно сделать на основе анализа кривой функции распределения времени пребывания

частиц в аппарате и соотношения его размеров. Исходя из соотношения размеров аппарата (L / d > 20), можно выбрать либо модель идеального вытеснения, либо однопараметрическую диффузионную модель. Из рисунка видно, что график дифференциальной функции, построенной по данным таблицы, соответствует однопараметрической диффузионной модели. Уравнение этой модели:

 

Начальные условия t = 0; c(x,0) = 0;

Граничные условия x = 0; c(0,t) = cвх;

моментов необходимо получить таблицу значений ti.

ti 1

3 5 7 9 11 13 15 17 19 21 23 25 27 29
ci 1 9.2 17.9 22.6 20.1 16.2 11.8 7.9 5.0 3.1 1.9 1.2 0.8 0.4 0.2

Эффективный объем аппарата V рассчитывается по формуле

Линейная скорость потока равна

Коэффициент продольного перемешивания Dx равен

 

 

 

распределения времени пребывания, полученную на основе экспериментальных данных. Эта функция

может быть охарактеризована ее числовыми характеристиками – моментами. Для определения моментов построенный график разбиваем по оси X на равные интервалы и методом прямоугольников находим площадь под кривой для каждого интервала.

ti = 1 … 29, t = 2, n = 14

Вычислим размерные моменты

 

0; c(0,t) = cвх;

сложно, поэтому для проверки адекватности модели перейдем к ячеечной модели.

Это допустимо, если

Число ячеек равно

Получили ячеечную модель с четырьмя ячейками, уравнения которой записываются следующим образом

 

 

 

 

получили систему четырех дифференциальных уравнений с четырьмя неизвестными, но нас

интересуют только значения концентрации на выходе последней ячейки, т.е. изменение концентрации c4. Систему решаем численным методом.
Сравнение экспериментальной кривой и расчетной функции распределения в последней ячейке дает возможность судить об адекватности модели.