Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Маслов Евгений Анатольевич доц., к.ф.-м.н. Кафедра
Содержание
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Маслов Евгений Анатольевич доц., к.ф.-м.н. Кафедра
- 2. СОДЕРЖАНИЕОСНОВЫ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 3.
- 3. 1. ОСНОВЫ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ3 ВВЕДЕНИЕ Основой метода
- 4. 2. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ (МКР) Одним из первых
- 5. ПРОДОЛЖЕНИЕ Формально проверить точность разностной аппроксимации производной можно,
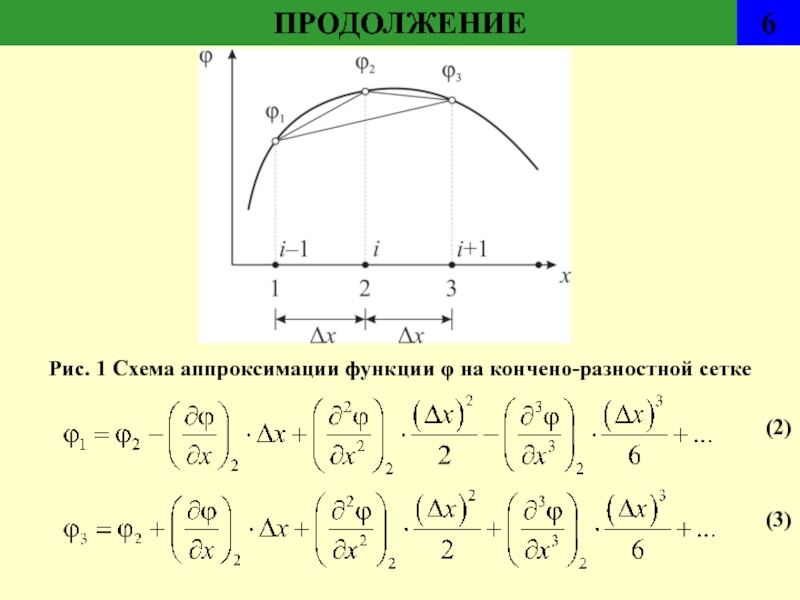
- 6. ПРОДОЛЖЕНИЕ 6(2)(3)
- 7. ПРОДОЛЖЕНИЕ Преобразуем выражением (3) к следующему виду:
- 8. ПРОДОЛЖЕНИЕ Тогда последнее выражение можно переписать в
- 9. ПРОДОЛЖЕНИЕ 9 Можно построить бесконечно много конечно-разностных
- 10. ПЕРЕРЫВ10 Рассмотрим аппроксимацию производных в двухмерном пространстве.
- 11. ПРОДОЛЖЕНИЕ11 Пусть φi,j = φ(x, y) см. рис. 3Рис. 3. Элемент двумерной конечно-разностной сетки Тогда
- 12. ПРОДОЛЖЕНИЕ12 Большинство уравнений в частных производных, встречающихся
- 13. 3. АППРОКСИМАЦИЯ ГРАНИЧНЫХ УСЛОВИЙ131. Граничные условия первого
- 14. ПРОДОЛЖЕНИЕ14 Представление граничного условия для процедуры решения
- 15. ПРОДОЛЖЕНИЕ15 Аналогична процедура представления граничного условия на
- 16. ПРОДОЛЖЕНИЕ16 Рис. 5. Расположение узлов в расчетной
- 17. ПРОДОЛЖЕНИЕ17 Разрешим следующую систему состоящую из аппроксимации
- 18. ПРОДОЛЖЕНИЕ18 Аналогична процедура представления граничного условия на
- 19. ПРОДОЛЖЕНИЕ19 Разрешим следующую систему состоящую из аппроксимации
- 20. ПРОДОЛЖЕНИЕ20 Рис. 6. Расположение узлов в расчетной
- 21. ЛИТЕРАТУРА Патанкар С. Численные методы решения задач
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Маслов Евгений Анатольевич
доц., к.ф.-м.н.
Кафедра атомных и тепловых электростанций
Корпус 4,
ауд 234
Слайд 2СОДЕРЖАНИЕ
ОСНОВЫ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
3. АППРОКСИМАЦИЯ ГРАНИЧНЫХ УСЛОВИЙ
ГРАНИЧНОЕ
УСЛОВИЕ ПЕРВОГО РОДА
ГРАНИЧНОЕ УСЛОВИЕ ВТОРОГО РОДА
ГРАНИЧНОЕ УСЛОВИЕ ТРЕТЬЕГО РОДА
2
Слайд 31. ОСНОВЫ МЕТОДА КОНЕЧНЫХ РАЗНОСТЕЙ
3
ВВЕДЕНИЕ
Основой метода конечных разностей (МКР)
является дискретизация – замена непрерывной области совокупностью изолированных точек (сеткой),
причем решение уравнений ищется лишь в этих точках (узлах сетки). Производные аппроксимируются конечными разностями и решение уравнения в частных производных сводится к решению системы линейных алгебраических уравнений (СЛАУ).Основные особенности получающейся СЛАУ определяются типом исходного уравнения в частных производных (или системы уравнений в частных производных). Стационарные задачи обычно сводятся к системам алгебраических уравнений, которые приходится решать одновременно во всей расчетной области, учитывая заданные граничные условия.
Слайд 42. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ (МКР)
Одним из первых шагов при применении
МКР к решению уравнения в частных производных является переход от
непрерывной области к конечно-разностной сетке.Для каждого уравнения в частных производных существует множество его конечно-разностных аналогов, из которых обычно нельзя выбрать наилучший со всех точек зрения. В первую очередь при использовании метода конечных разностей надо стремиться к правильной аппроксимации уравнений поставленной задачи, а во вторую очередь выбрать «наилучшую» схему, т. е. оптимизировать ее, учитывая ее точность, экономичность, удобство программной реализации на ЭВМ и т. д.
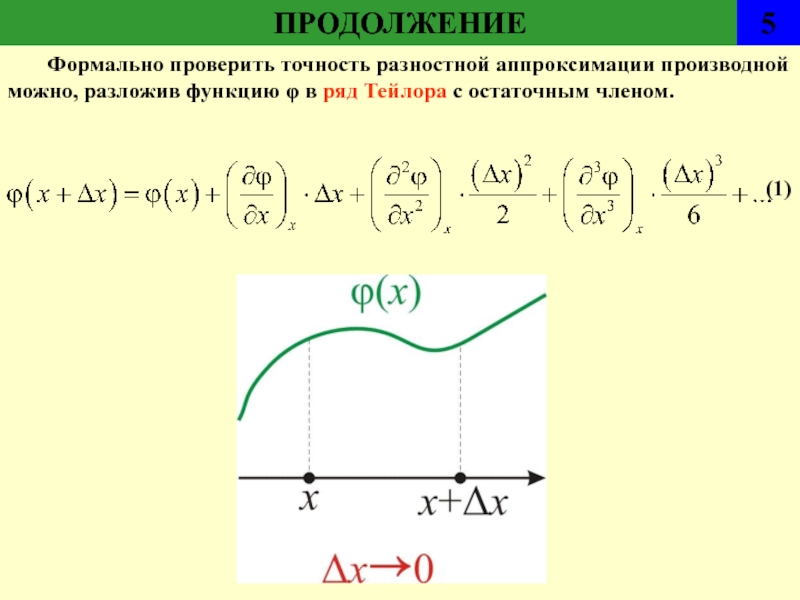
Для того чтобы лучше понять идею конечно-разностной аппроксимации производных, вспомним определение производной от функции например одной переменной φ(х) в произвольной точке:
Если функция φ(х) непрерывна, а Δх — достаточно мало, но конечно, то значение разности [φ(x+Δх) – φ(x)] / Δх будет близко к значению производной ∂φ / ∂x. Действительно, из теоремы о конечном приращении следует, что разностное значение производной равно производной искомой функции в некоторой точке интервала длины Δх.
4
Слайд 5ПРОДОЛЖЕНИЕ
Формально проверить точность разностной аппроксимации производной можно, разложив функцию φ
в ряд Тейлора с остаточным членом.
5
(1)
Слайд 7ПРОДОЛЖЕНИЕ
Преобразуем выражением (3) к следующему виду:
или
Таким образом, получим
где
разность (φ3–φ2)/Δх, очевидно, является конечно-разностным представлением производной (∂φ/∂x)2. Погрешностью аппроксимации
называется разность значений частной производной и ее конечно-разностного аналога. Можно характеризовать погрешность аппроксимации стандартным математическим обозначением порядка малой величины (O).7
(4)
(5)
Слайд 8ПРОДОЛЖЕНИЕ
Тогда последнее выражение можно переписать в виде
где О(Δх)
имеет точный математический смысл. Представление погрешности аппроксимации в виде О(Δх)
обозначает, что погрешность аппроксимации по абсолютной величине не превосходит K∙|Δх| при Δх → 0 (для достаточно малых Δх), причем К > 0 — вещественная константа. Практически порядок погрешности аппроксимации в этом случае равен Δх и является самой высокой степенью, общей для всех членов уравнения. Таким образом представление производной в следующей формеявляется приближенным, погрешность приближения равна погрешности аппроксимации Δх и называется «правой» разностью.
Отметим, что представление погрешности аппроксимации в виде О(Δх) ничего не говорит о величине погрешности, а лишь указывает на характер ее стремления к нулю. Если погрешность другой конечно-разностной аппроксимации производной равна O(Δх2), то можно ожидать, что во втором случае погрешность аппроксимации будет меньше, чем в первом. Это утверждение безусловно верно для достаточно малых Δх, но какое Δх будет «достаточно малым», определить заранее сложно.
8
(6)
(7)
Слайд 9ПРОДОЛЖЕНИЕ
9
Можно построить бесконечно много конечно-разностных аппроксимаций производной (∂φ/∂x)2.
Построим аппроксимацию этой производной с использованием разностей назад (их называют
также «левыми» разностями) используя выражение (2), тогдаВычитая соотношение (2) из соотношения (3), получим аппроксимацию производной центральными разностями
Складывая выражение (2) и (3), найдем конечно-разностную аппроксимацию производной второго порядка
(8)
(9)
(10)
Слайд 10ПЕРЕРЫВ
10
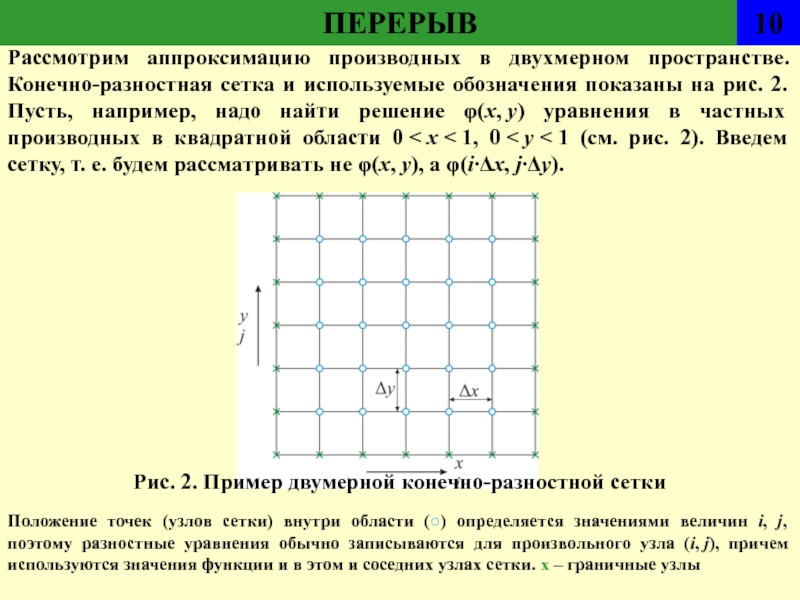
Рассмотрим аппроксимацию производных в двухмерном пространстве. Конечно-разностная сетка и
используемые обозначения показаны на рис. 2. Пусть, например, надо найти
решение φ(х, у) уравнения в частных производных в квадратной области 0 < х < 1, 0 < y < 1 (см. рис. 2). Введем сетку, т. е. будем рассматривать не φ(х, у), a φ(i∙Δх, j∙Δу).Положение точек (узлов сетки) внутри области (○) определяется значениями величин i, j, поэтому разностные уравнения обычно записываются для произвольного узла (i, j), причем используются значения функции и в этом и соседних узлах сетки. х – граничные узлы
Слайд 11ПРОДОЛЖЕНИЕ
11
Пусть φi,j = φ(x, y) см. рис. 3
Рис. 3. Элемент двумерной конечно-разностной
сетки
Тогда
Слайд 12ПРОДОЛЖЕНИЕ
12
Большинство уравнений в частных производных, встречающихся в гидродинамике и
теплопередаче, содержат лишь частные производные первого и второго порядков, при
этом для аппроксимации производных стараются использовать не более трех узлов разностной сетки. Поэтому на равномерной сетке чаще всего применяют приведенные ниже конечно-разностные аппроксимации первых производных.(11)
(12)
(13)
(14)
(или)
(или)
(или)
(или)
Слайд 133. АППРОКСИМАЦИЯ ГРАНИЧНЫХ УСЛОВИЙ
13
1. Граничные условия первого рода – задается
распределение температуры на поверхности (или границе) тела для каждого момента
времени:Т(x, y, t)=TW,
(15)
где TW – температура на поверхности тела (на границе). Во многих практически значимых вариантах TW = const.
Рис. 4. Расположение узлов в расчетной области решения: × – узлы на границе расчетной области; ○ – узлы внутри расчетной области
Математическое представление граничного условия:
t > 0, x = 0, y = yfix: Т(x, y, t)=TW.
Аппроксимация граничного условия на расчетной сетке в узле (i = 0):
Т0,j = TW.
(16)
(17)
Слайд 14ПРОДОЛЖЕНИЕ
14
Представление граничного условия для процедуры решения СЛАУ – методом
прогонки. Для этого запишем разностный шаблон (см. лекция 1, формула
(2) для i = 0), для простоты выкладок опустим индекс j:a0∙T–1 + b0∙T0 + c0∙T1 = d0.
Теперь необходимо подобрать, такой набор значений коэффициентов (a0, b0, c0, d0) входящих в (18), чтобы получившееся выражение соответствовало выражению (17). Для этого необходимо решить совместно эти два равенства и найти значения коэффициентов, выпишем эту систему:
очевидно, что значение температуры T–1 – выходит за границу области решения, поэтому необходимо принять a0 = 0. Значение a0 = 0 принимается всегда, независимо от вида граничного условия. Затем коэффициент b0 = 1, c0 = 0 и d0 = TW.
(18)
(19)
Слайд 15ПРОДОЛЖЕНИЕ
15
Аналогична процедура представления граничного условия на правой границе области
решения.
очевидно, что значение температуры TN+1 – выходит за границу области
решения, поэтому необходимо принять cN = 0. Значение cN = 0 принимается всегда, независимо от вида граничного условия. Затем коэффициент aN = 0,
bN = 1,и dN = TW.2. Граничные условия второго рода – задается значение удельного теплового потока для каждой точки поверхности (или границы) тела в любой момент времени (закон Фурье):
где n – нормаль к поверхности тела, qW – удельный тепловой поток (Вт/м2). Наиболее часто используется условие qW = const.
(20)
Слайд 16ПРОДОЛЖЕНИЕ
16
Рис. 5. Расположение узлов в расчетной области решения: ×
– узлы на границе расчетной области; ○ – узлы внутри
расчетной областиМатематическое представление граничного условия:
t > 0, x = 0, y = yfix:
знак «–» означает, что происходит подвод тепла в расчетную область.
Аппроксимация граничного условия на расчетной сетке в узле (i = 0) будем осуществлять левой конечной разностной схемой (11):
(21)
(22)
Слайд 17ПРОДОЛЖЕНИЕ
17
Разрешим следующую систему состоящую из аппроксимации граничного условия (22)
и разностного шаблона (18) относительно коэффициентов (a0, b0, c0, d0):
для
этого преобразуем верхнее выражение в системе (23), получимТогда необходимо принять следующие коэффициенты разностного шаблона:
(23)
(24)
Слайд 18ПРОДОЛЖЕНИЕ
18
Аналогична процедура представления граничного условия на правой границе области
решения.
Математическое представление граничного условия:
t > 0, x = L, y = yfix:
знак «+» означает, что
происходит отвод тепла из расчетной области.Аппроксимация граничного условия на расчетной сетке в узле (i = N) будем осуществлять левой конечной разностной схемой (11):
или
(25)
(26)
Слайд 19ПРОДОЛЖЕНИЕ
19
Разрешим следующую систему состоящую из аппроксимации граничного условия (26)
и разностного шаблона (20) относительно коэффициентов (aN, bN, cN, dN):
Тогда
необходимо принять следующие коэффициенты разностного шаблона: 3. Граничные условия третьего рода – задается взаимосвязь между потоком тепла за счет теплопроводности от твердой стенки и тепловым потоком из окружающей среды за счет температурного напора (закон Ньютона – Рихмана) [1]:
где αe – коэффициент теплообмена (Вт/(м2·ºС)), Te – температура окружающей среды вблизи поверхности тела.
(27)
(28)
Слайд 20ПРОДОЛЖЕНИЕ
20
Рис. 6. Расположение узлов в расчетной области решения: ×
– узлы на границе расчетной области; ○ – узлы внутри
расчетной областиЛевая граница Правая граница
Слайд 21ЛИТЕРАТУРА
Патанкар С. Численные методы решения задач теплообмена и динамики
жидкости. – М.: Энергоатомиздат, 1984. – 152 с.
Андерсон Д., Таннехилл
Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: В 2-х т., Т. 1: Пер. с англ. — М.: Мир, 1990. — 384 с., ил. ISBN 5-03-001927-8 Численные методы. Сборник задач: учеб. Пособие для вузов / В.Ю. Гидаспов, И.Э. Иванов, Д.Л. Ревизников и др.; под ред. У.Г. Пирумова. — М.: Дрофа, 2007. — 144 с.: ил. ISBN 978-5-358-01310-0
21