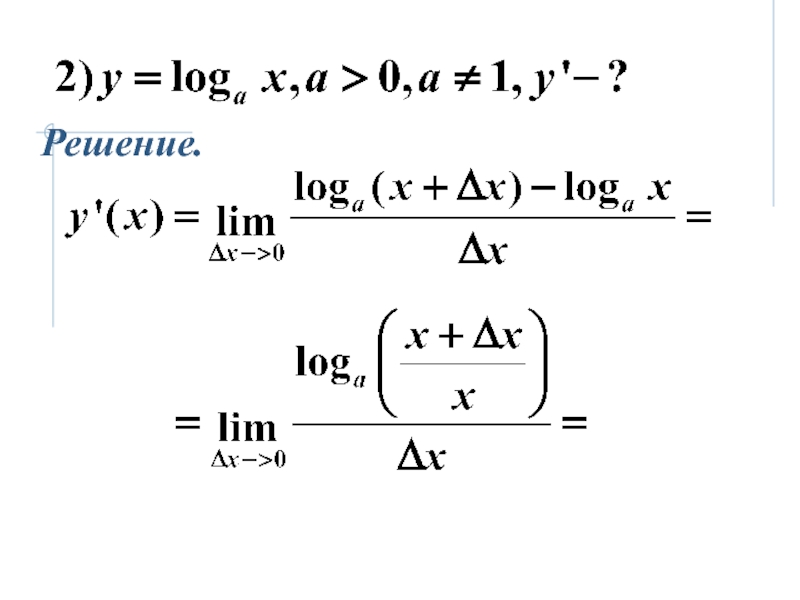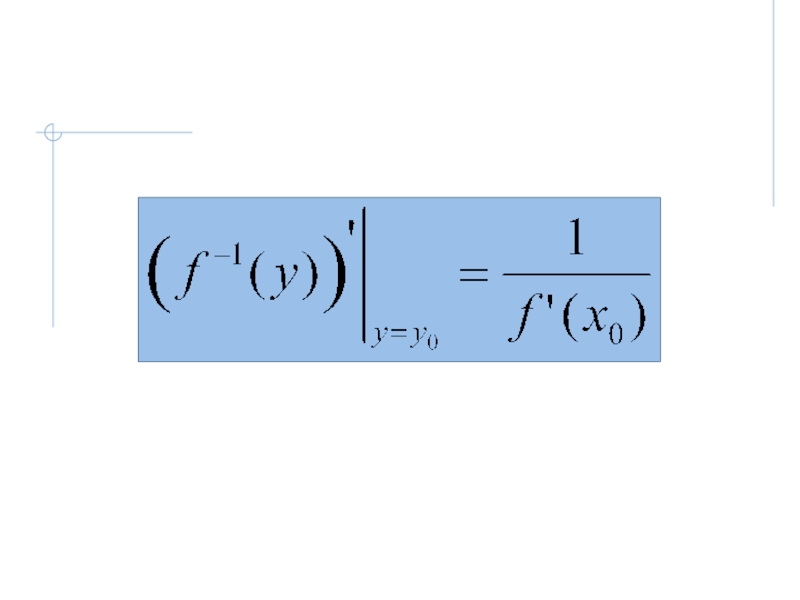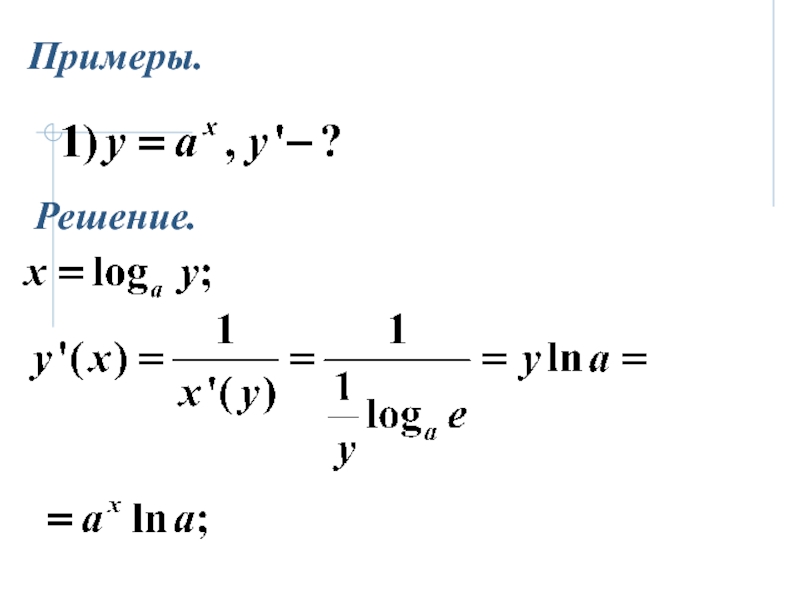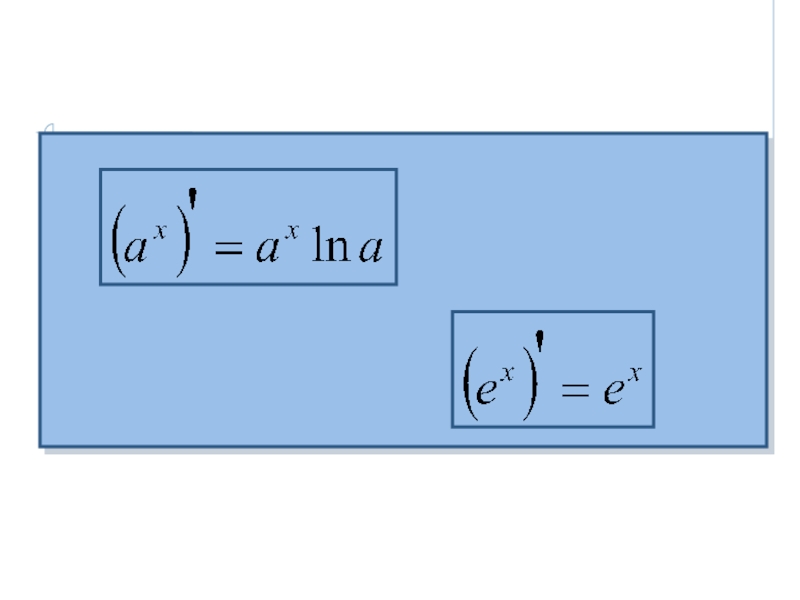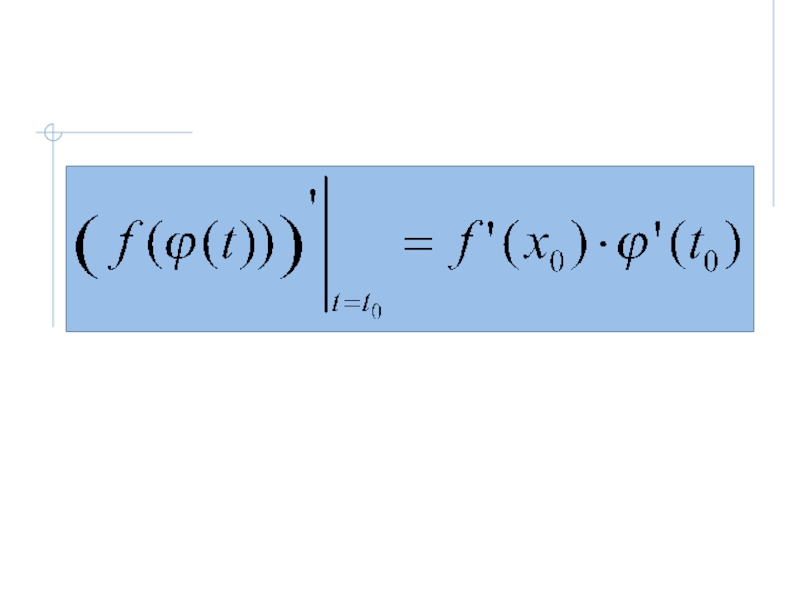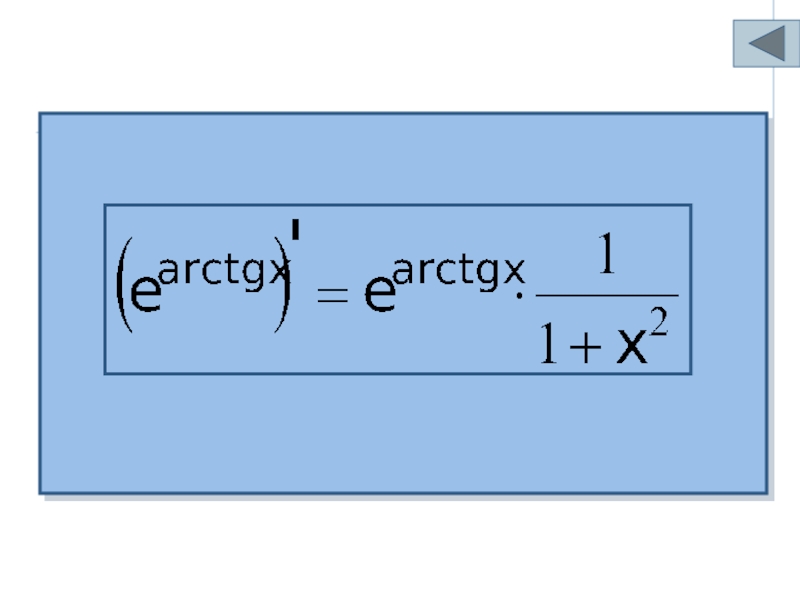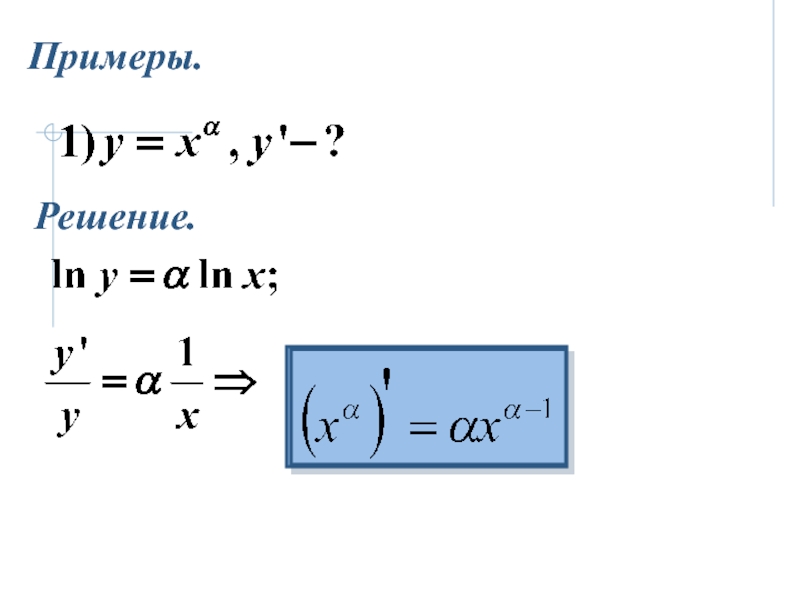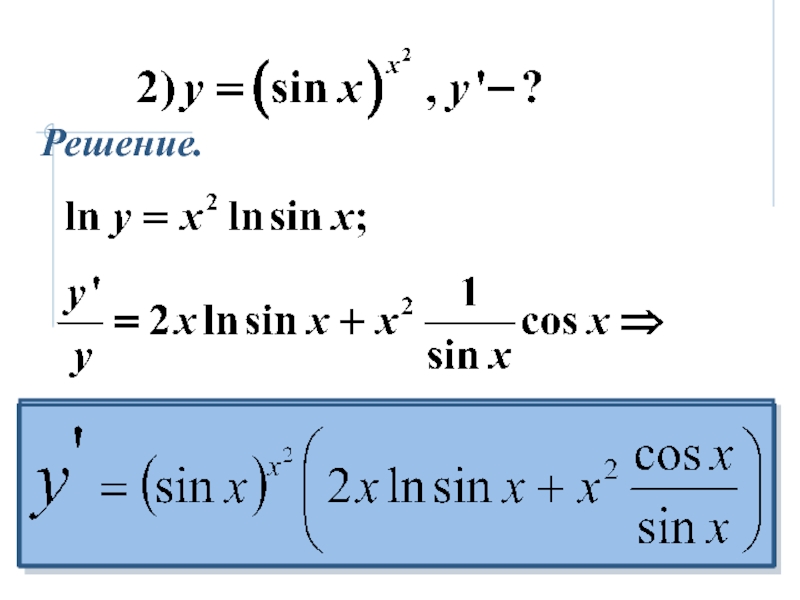Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика Часть 1
Содержание
- 1. Математика Часть 1
- 2. Лекция 102. Геометрический смысл производной 3. Механический
- 3. 9. Производная функции, заданной параметрически6.
- 4. 1. Производная функцииПусть f(x) определена на (a,b),
- 5. Слайд 5
- 6. Примеры вычисления y'(x). Решение.
- 7. Слайд 7
- 8. Решение.
- 9. Слайд 9
- 10. Слайд 10
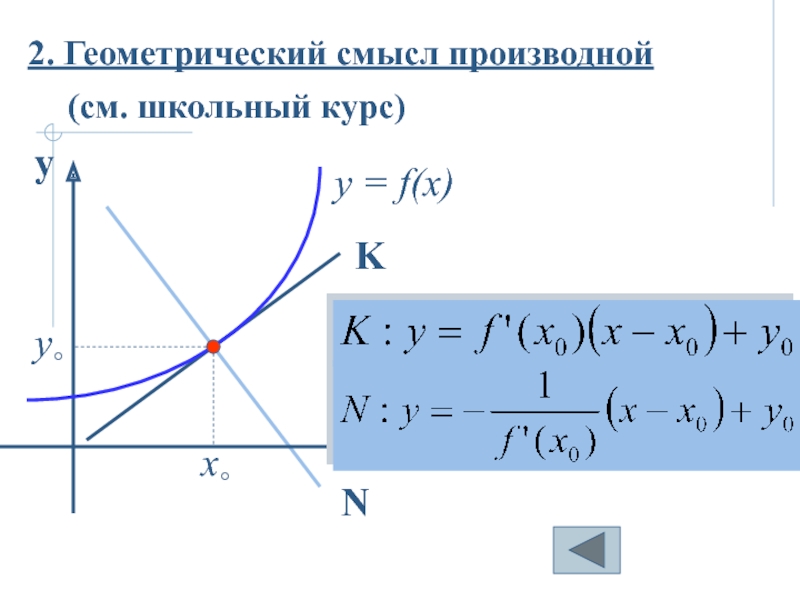
- 11. 2. Геометрический смысл производной(см. школьный курс)x° y°
- 12. 3. Механический смысл производной(см. школьный курс)- мгновенная скорость
- 13. 4. Правила и формулы дифференцирования.
- 14. Пример. Решение.
- 15. 5. Производная обратной функции.Если:
- 16. Тогда: в окрестности точки
- 17. Доказательство
- 18. Слайд 18
- 19. Слайд 19
- 20. Примеры.Решение.
- 21. Слайд 21
- 22. Решение.
- 23. Слайд 23
- 24. Слайд 24
- 25. 6. Производная сложной функции.Если
- 26. Тогда:
- 27. Доказательство. Рассмотрим Пусть тогдаТогда
- 28. Вычислим
- 29. Слайд 29
- 30. Замечание.В теореме t - независимая переменная, x - промежуточный аргумент.На практике чаще имеем дело с функциями вида
- 31. Пример.Решение.
- 32. Слайд 32
- 33. 7. Производная неявной функции.Пример.Решение. а)Переход к явной функции
- 34. б)Правило.Чтобы найти первую производную функции, заданной неявно, нужно один раз продифференцировать выражение, задающее функцию по x.
- 35. 8. Логарифмическое дифференцирование -прием предварительного логарифмирования выражения
- 36. Примеры.Решение.
- 37. Решение.
- 38. Решение.
- 39. 9. Производная функции, заданной параметрически.Здесь y зависит от x через параметр t; Если:
- 40. Тогда: Доказательство.
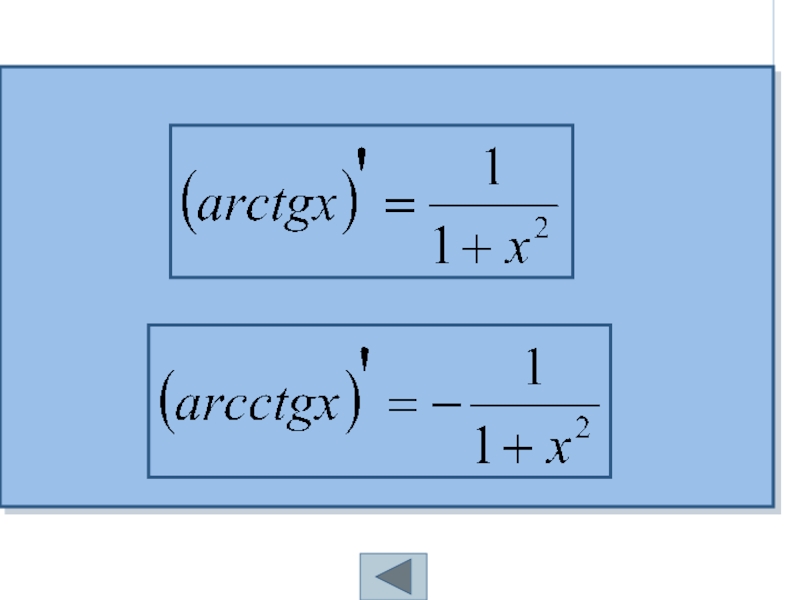
- 41. Таблица производных
- 42. Гиперболический синус: Гиперболический косинус: Гиперболический тангенс: Гиперболический котангенс:
- 43. Скачать презентанцию
Лекция 102. Геометрический смысл производной 3. Механический смысл производнойПравила и формулы дифференцирования 5. Производная обратной функции 1. Производная функции
Слайды и текст этой презентации
Слайд 2Лекция 10
2. Геометрический смысл производной
3. Механический смысл производной
Правила и
формулы
функции
Слайд 39. Производная функции, заданной
параметрически
6. Производная сложной
функции
7. Производная неявной функции
8. Логарифмическое дифференцирование
Слайд 41. Производная функции
Пусть f(x) определена на (a,b),
x
(a,b) - некоторая фиксированная точка,
x - любое число:
x + x (a,b). x - приращение аргумента в точке x,
y = f(x+ x) - f(x) - приращение функции
в точке x.
Слайд 30Замечание.
В теореме t - независимая переменная,
x - промежуточный аргумент.
На практике
чаще имеем дело с функциями вида
Слайд 34б)
Правило.
Чтобы найти первую производную функции, заданной неявно, нужно один раз
продифференцировать выражение, задающее функцию по x.
Слайд 358. Логарифмическое дифференцирование -
прием предварительного логарифмирования выражения при вычислении его
производной:
Решение.
а)Логарифмирование выражения
здесь y - неявная функция.
Слайд 399. Производная функции, заданной
параметрически.
Здесь y зависит от x через
параметр t;
Если:
Слайд 42 Гиперболический синус:
Гиперболический косинус:
Гиперболический тангенс:
Гиперболический котангенс:
