Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика ППИ
Содержание
- 1. Математика ППИ
- 2. УЧЕБНЫЕ ВОПРОСЫ1. Уравнения, допускающие понижение порядка, их интегрирование. 2. Линейные ДУ второго порядка, однородные и неоднородные.
- 3. Литература[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
- 4. Учебный вопрос.Уравнения, допускающие понижение порядка.
- 5. Уравнения, допускающие понижение порядка.
- 6. Уравнения, допускающие понижение порядка, их интегрирование. 1.
- 7. Далее, аналогично находим
- 8. Слайд 8
- 9. 2. Дифференциальное уравнение второго порядка вида
- 10. ПримерНайти решение дифференциального уравнения
- 11. Слайд 11
- 12. 3. Дифференциальное уравнение второго порядка вида
- 13. Пример.Найти решение дифференциального уравненияРешение.
- 14. Слайд 14
- 15. Интегрирование ДУ движения авиабомбы без учета
- 16. Положение авиабомбы после сброса в момент
- 17. Подставим начальные условия
- 18. Решаем уравнение для функции х,Из начальных условий
- 19. Таким образом, координаты положения авиабомбы характеризуются уравнениямиИсключим
- 20. Учебный вопрос.ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ОДНОРОДНЫЕ И НЕОДНОРОДНЫЕ
- 21. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ОДНОРОДНЫЕ
- 22. Теорема (о структуре общего решения
- 23. Теорема (о структуре общего решения однородного уравнения).
- 24. Определение. Система { у1 (х), у2(х) },
- 25. Существуют общие методы нахождения ФСР. Один из
- 26. Полученное квадратное уравнение называется характеристическим уравнением однородного
- 27. 1. Составим характеристическое уравнение
- 28. 2. Если корни k1 и k2 характеристического
- 29. Пример. Найти общее решение дифференциального уравнения
- 30. Задание на самостоятельную работу[2] Н.С. Пискунов. Дифференциальное
- 31. Я́коб Берну́лли (27.12.1654-16.08.1705), Базель, Швейцария. Якобу Бернулли принадлежат значительные достижения
- 32. учебный вопросРассмотрим случай, когда в уравнениифункции p(x) и g(x) – постоянные величины.
- 33. Уравнение виданазывается линейным ДУ с постоянными коэффициентами1
- 34. Где у – искомая функция, p, g
- 35. Рассмотрим сначала однородное уравнение:Будем искать решение этого
- 36. Это уравнение называется характеристическим уравнением для уравнения (1).
- 37. ПРИМЕРЫ.Решить дифференциальное уравнение:1
- 38. Решение:Корни вещественные и разные, поэтому общее решение будет иметь вид:
- 39. Решить дифференциальное уравнение:2
- 40. Решение:Корни вещественные и одинаковые, поэтому общее решение будет иметь вид:
- 41. Решить дифференциальное уравнение:3
- 42. Решение:Корни комплексные, поэтому общее решение будет иметь вид:
- 43. Теперь рассмотрим решение неоднородного ЛДУ с постоянными
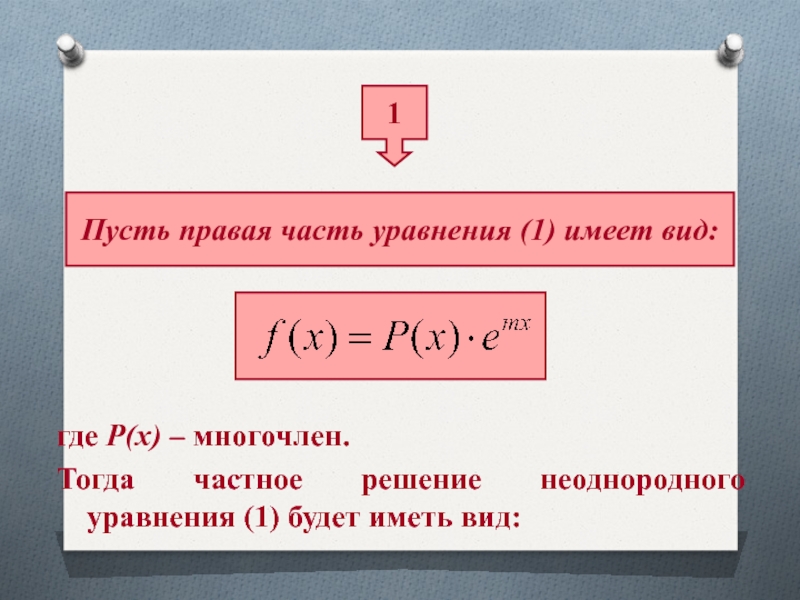
- 44. 1Пусть правая часть уравнения (1) имеет вид:где
- 45. где Q(х) – многочлен той же степени,
- 46. ПРИМЕР.Решить дифференциальное уравнение:
- 47. Решение:Корни вещественные и одинаковые, поэтому общее решение однородного уравнения будет иметь вид:Сначала решаем однородное уравнение:
- 48. Теперь решаем неоднородное уравнение. Правая часть представляет
- 49. Находим производные и подставляем в исходное уравнение:Частное решение неоднородного уравнения имеет вид:
- 50. Общее решение неоднородного уравнения запишем как сумму общего решения однородного уравнения и частного решения неоднородного уравнения:
- 51. 2Пусть правая часть уравнения (1) имеет вид:
- 52. Если числане являются корнями характеристического уравнения, то
- 53. ПРИМЕР.Решить дифференциальное уравнение:
- 54. Решение:Сначала решаем однородное уравнение:
- 55. Корни комплексные, поэтому общее решение будет иметь
- 56. Находим производные и подставляем в исходное уравнение:
- 57. Частное решение неоднородного уравнения имеет вид:Общее решение
- 58. 3Пусть правая часть уравнения (1) имеет вид:где Р1(х) и Р2(х) – многочлены.
- 59. Если числане являются корнями характеристического уравнения, то
- 60. где R1(х) и R2(х) – многочлены той
- 61. учебный вопрос.Решить дифференциальное уравнение:
- 62. Решение:Сначала находим общее решение однородного уравнения:
- 63. Корни вещественные и разные, поэтому общее решение
- 64. Пусть Тогда Подставляем в уравнение:
- 65. Получаем:
- 66. Вычитаем из второго уравнения первое:Теперь подставляем в первое уравнение:
- 67. Интегрируем эти выражения:Частное решение неоднородного уравнения имеет вид:Общее решение будет:
- 68. Скачать презентанцию
УЧЕБНЫЕ ВОПРОСЫ1. Уравнения, допускающие понижение порядка, их интегрирование. 2. Линейные ДУ второго порядка, однородные и неоднородные.
Слайды и текст этой презентации
Слайд 2УЧЕБНЫЕ ВОПРОСЫ
1. Уравнения, допускающие понижение порядка, их интегрирование.
2. Линейные
ДУ второго порядка, однородные и неоднородные.
Слайд 3Литература
[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2. Москва:
Интеграл-Пресс, 2005. с. 13-90;
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий курс
высшей математики. Москва: Издательство АСТ, 2004. с. 446-490Слайд 6Уравнения, допускающие понижение порядка, их интегрирование.
1. Простейшим уравнением n-го порядка
является уравнение вида
Найдём общий интеграл этого уравнения.
Интегрируем по x левую и правую части и принимая во внимание, что , получим
,
где С1 постоянная интегрирования.
Слайд 92. Дифференциальное уравнение второго порядка вида
,
не содержащее искомой функции у ,
с помощью подстановки
,
преобразуется в уравнение первого порядка
.
Слайд 12
3. Дифференциальное уравнение второго порядка вида
,
не содержащее независимой переменной x, с помощью подстановки
сводится к уравнению первого порядка
.
Слайд 15 Интегрирование ДУ движения авиабомбы без учета сопротивления воздуха.
Найдем траекторию
движения
авиационной бомбы, брошенной
с самолета на
скорости V0, падающей под действием
одной только силы тяжести
(сопротивлением воздуха
пренебрегаем).
Слайд 16
Положение авиабомбы после сброса в момент времени t будет
задаваться координатами x и у. Будем считать, что
Т.к.
рассматривается движение без сопротивления воздуха, при t=0 имеем x=0, y=0,Решим дифференциальные уравнения,
поскольку , то , тогда
Слайд 19Таким образом, координаты положения авиабомбы характеризуются уравнениями
Исключим параметр t:
и
.Траектория движения авиабомбы без учета сопротивления воздуха представляет собой параболу .
Слайд 20Учебный вопрос.
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ОДНОРОДНЫЕ И НЕОДНОРОДНЫЕ
Слайд 21 ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ОДНОРОДНЫЕ И НЕОДНОРОДНЫЕ
Определение. Линейное
неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами имеет
видгде действительные числа; f(х) – непрерывная функция.
Определение. Если то уравнение
называется однородным дифференциальным уравнением (ЛОДУ), соответствующим данному неоднородному.
Слайд 22 Теорема (о структуре общего решения неоднородного уравнения).
Если известно
какое-либо частное решение yчн неоднородного уравнения, то его общее решение
равно сумме общего решения однородного уравнения yо и частного решения неоднородного yчн:Слайд 23Теорема (о структуре общего решения однородного уравнения).
Если у1(х) и
у2(х) - частные решения уравнения ЛОДУ, причем отношение
(по-другому, у1(х) и у2(х) - линейно независимые решения), то их линейная комбинация есть общее решение yо этого уравнения:
yо= у1(х) С1 + у2(х) С2.
Слайд 24Определение. Система { у1 (х), у2(х) }, функции которой удовлетворяют
условиям теоремы 2, называется фундаментальной системой решений (ФСР) ЛОДУ уравнения
2-го порядка.Слайд 25Существуют общие методы нахождения ФСР. Один из них это метод
Эйлера. Суть его в следующем.
Решением однородного уравнения может быть
экспоненциальная функция вида так как она сохраняет свой вид при дифференциро-вании: и , где к – постоянная.Подставив в однородное уравнение, имеем
Слайд 26Полученное квадратное уравнение называется характеристическим уравнением однородного уравнения. Решив характеристическое
уравнение, построим ФСР. Таким образом, найдем все частные решения уравнения
однородного уравнения.Постановка задачи.
Найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами
Слайд 271. Составим характеристическое уравнение
.
Найдем его корни k1 и k2.
2. В зависимости от значений k1 и k2 , построим ФСР и запишем общее решение однородного уравнения. При этом выделяют три случая:
1) Если корни k1 и k2 характеристического уравнения действительные и , тогда ФСР имеет вид { } и общее решение запишется так
Слайд 282. Если корни k1 и k2 характеристического уравнения действительные
и , тогда
ФСР имеет вид и общее решение запишется так .3. Если характеристическое уравнение имеет комплексно – сопряженные корни:
тогда ФСР имеет вид и общее решение запишется так
Слайд 29Пример. Найти общее решение дифференциального уравнения
Решение.
1.
Составим характеристическое уравнение
Решим полученное квадратное уравнение:
2. Так
как и - комплексно – сопряженные корни, тогда ФСР имеет вид и общее решение
запишется так
Слайд 30Задание на самостоятельную работу
[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления.
Т 2. Москва: Интеграл-Пресс, 2005. с. 13-90;
[3] Б.П. Демидович, В.А.
Кудрявцев. Краткий курс высшей математики. Москва: Издательство АСТ, 2004. с. 446-490Слайд 31Я́коб Берну́лли (27.12.1654-16.08.1705), Базель, Швейцария.
Якобу Бернулли принадлежат
значительные достижения
в теории рядов,
дифференциальном исчислении,
теории вероятностей и теории чисел, где его
именем
названы «числа Бернулли».
Слайд 32 учебный вопрос
Рассмотрим случай, когда в уравнении
функции p(x) и g(x)
– постоянные величины.
Слайд 34Где у – искомая функция, p, g – постоянные величины.
Если
f(х)=0, то уравнение называется
линейным однородным.
Если f (х) не равно 0,
то уравнение называется линейным неоднородным.
Слайд 35Рассмотрим сначала однородное уравнение:
Будем искать решение этого уравнения в виде
Где
k - некоторое число.
Находим производные и подставляем в исходное уравнение:
2
Слайд 43Теперь рассмотрим решение неоднородного ЛДУ с постоянными коэффициентами (1).
Общее решение
неоднородного ЛДУ
с постоянными коэффициентами
находится как сумма общего решения
однородного уравнения и
какого-либочастного решения неоднородного
уравнения.
Слайд 441
Пусть правая часть уравнения (1) имеет вид:
где Р(х) – многочлен.
Тогда частное решение неоднородного уравнения (1) будет иметь вид:
Слайд 45где Q(х) – многочлен той же степени, что и Р(х).
Причем, если m не является корнем характеристического уравнения, то
r=0,
а если является, то r – кратность этого корня.


![Математика ППИ Литература[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2. Москва: Интеграл-Пресс, Литература[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2. Москва: Интеграл-Пресс, 2005. с. 13-90;[3] Б.П. Демидович, В.А.](/img/thumbs/f1f88a2fb09b71ebe4a2143b3ec75dd7-800x.jpg)


























![Математика ППИ Задание на самостоятельную работу[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т Задание на самостоятельную работу[2] Н.С. Пискунов. Дифференциальное и интегральное исчисления. Т 2. Москва: Интеграл-Пресс, 2005. с. 13-90;[3]](/img/thumbs/96b0bd4efd2a5ecdfe4e96c575236584-800x.jpg)