Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
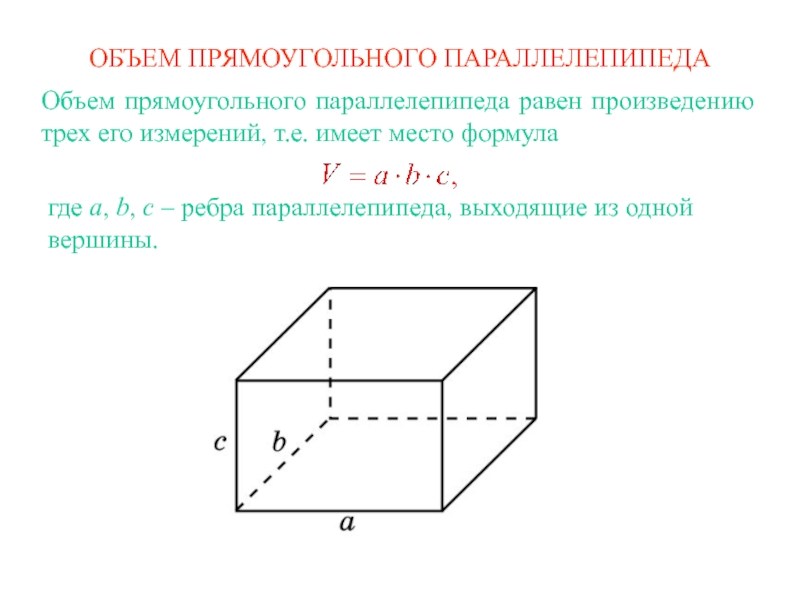
ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
Содержание
- 1. ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
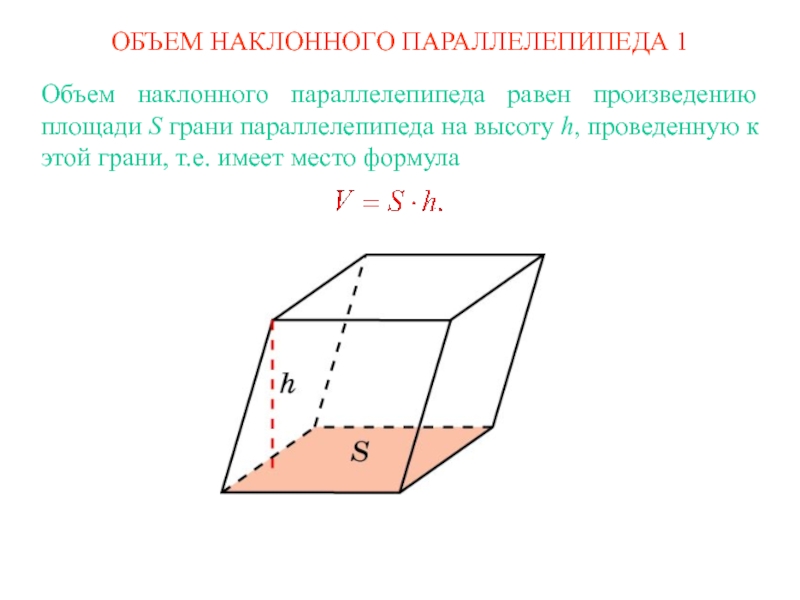
- 2. ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 1Объем наклонного параллелепипеда равен
- 3. ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 2Если ребро параллелепипеда равно
- 4. ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 3Пусть ребра параллелепипеда, выходящие
- 5. Упражнение 1Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите объем параллелепипеда.Ответ: 6.
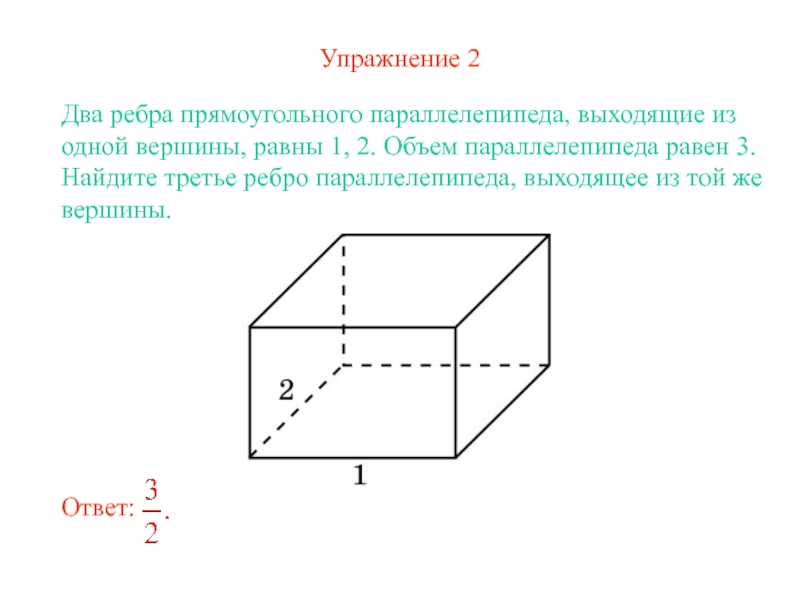
- 6. Упражнение 2Два ребра прямоугольного параллелепипеда, выходящие из
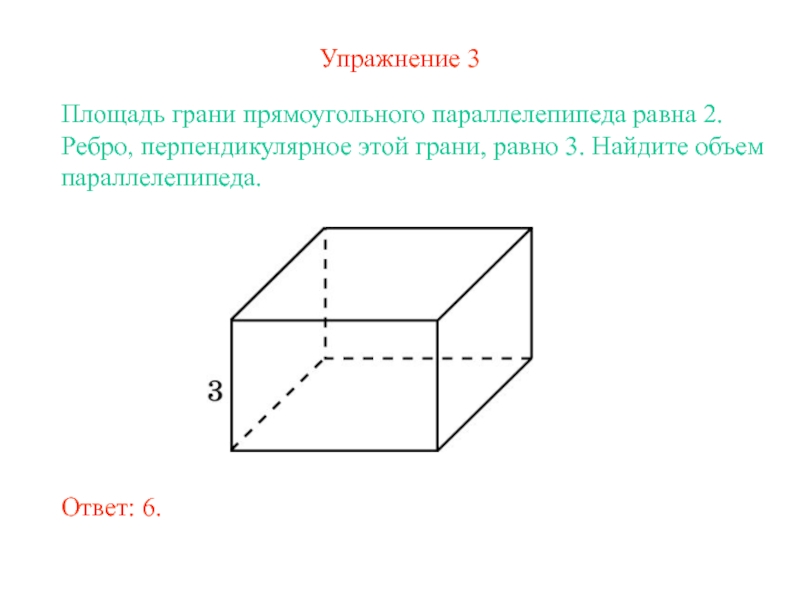
- 7. Упражнение 3Площадь грани прямоугольного параллелепипеда равна 2.
- 8. Упражнение 4Два ребра прямоугольного параллелепипеда, выходящие из
- 9. Упражнение 5Диагональ куба равна 1. Найдите его объем.
- 10. Упражнение 6Во сколько раз увеличится объем куба,
- 11. Упражнение 7Площадь поверхности куба равна 1. Найдите его объем.
- 12. Упражнение 8Если каждое ребро куба увеличить на
- 13. Упражнение 9Два ребра прямоугольного параллелепипеда, выходящие из
- 14. Упражнение 10Ребро прямоугольного параллелепипеда равно 1. Диагональ
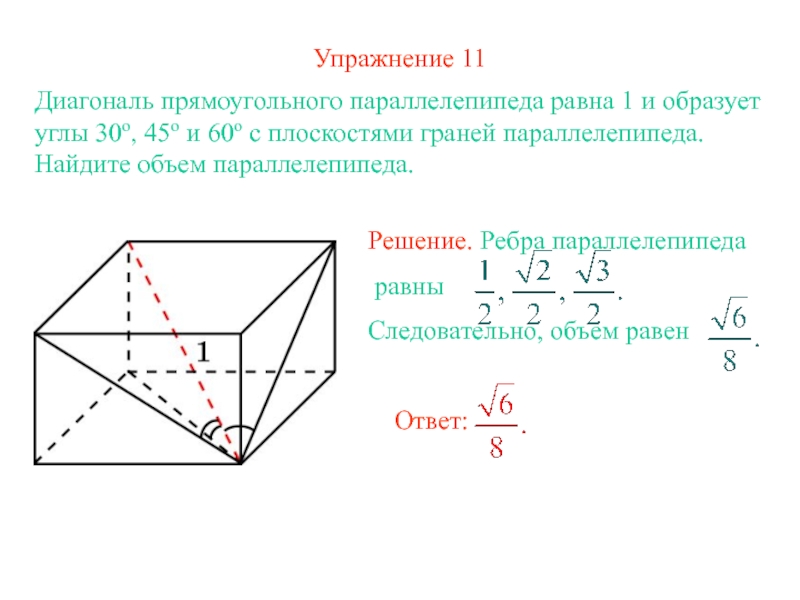
- 15. Упражнение 11Диагональ прямоугольного параллелепипеда равна 1 и
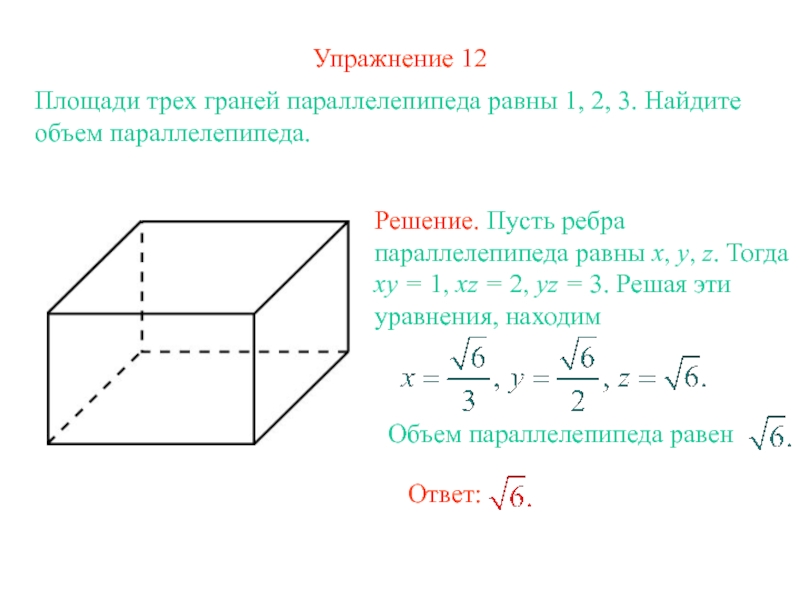
- 16. Упражнение 12Площади трех граней параллелепипеда равны 1, 2, 3. Найдите объем параллелепипеда.
- 17. Упражнение 13Две противоположные грани параллелепипеда – квадраты
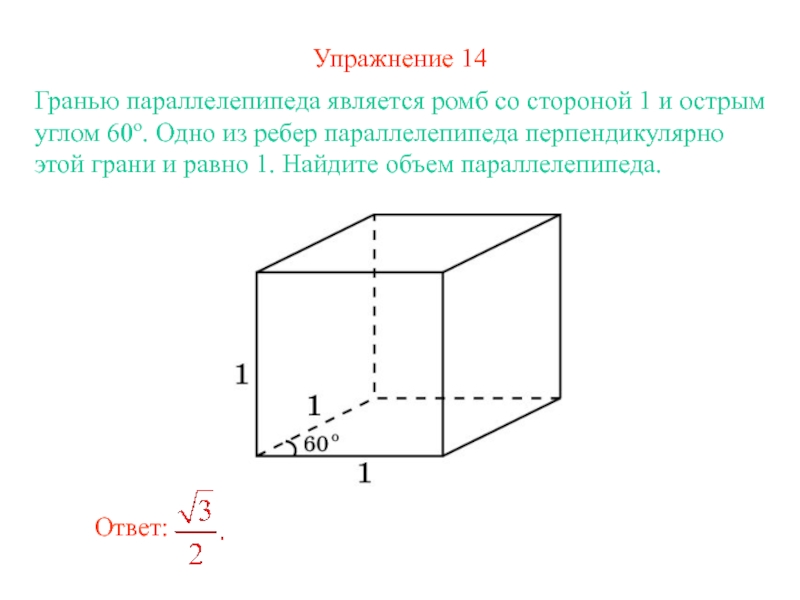
- 18. Упражнение 14Гранью параллелепипеда является ромб со стороной
- 19. Упражнение 15Гранью параллелепипеда является ромб со стороной
- 20. Упражнение 16Три грани параллелепипеда, имеющие общую вершину,
- 21. Упражнение 17В параллелепипеде две грани имеют площади
- 22. Упражнение 18В параллелепипеде две грани являются прямоугольниками
- 23. Упражнение 19Прямоугольный параллелепипед описан около цилиндра, радиус
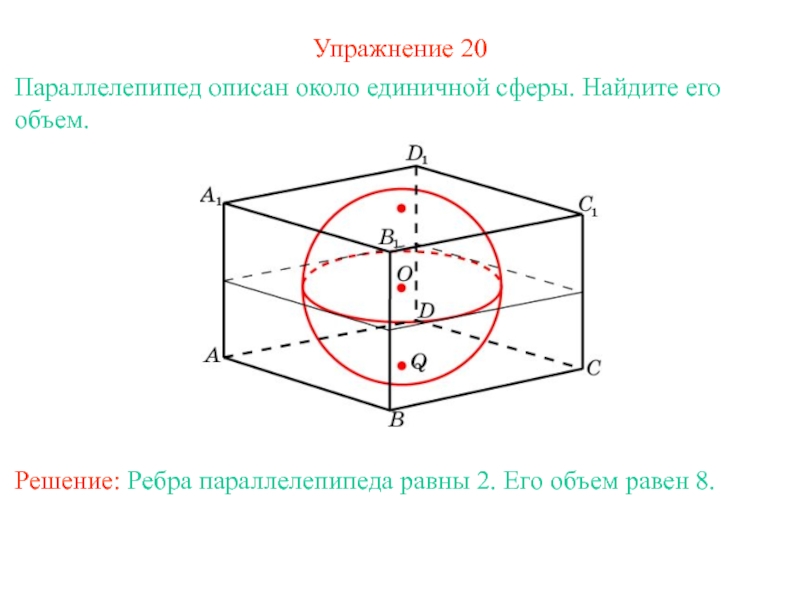
- 24. Упражнение 20Параллелепипед описан около единичной сферы. Найдите его объем.
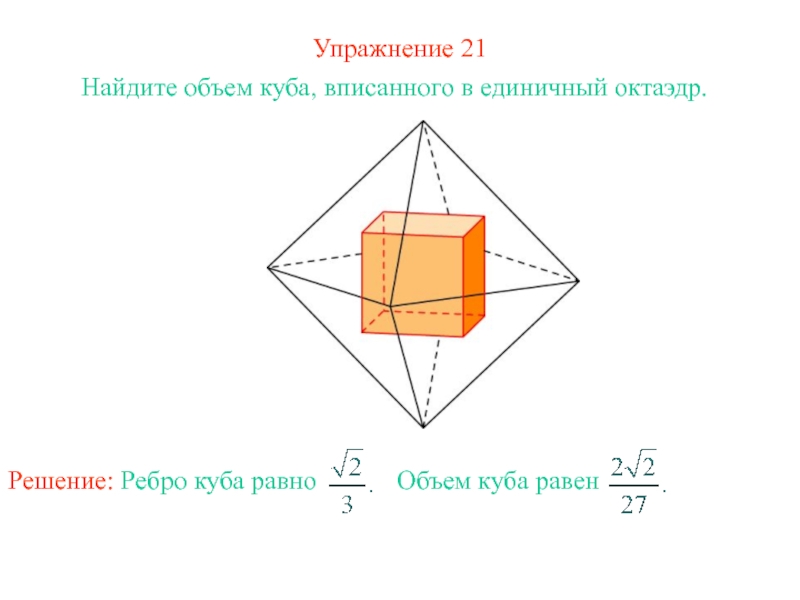
- 25. Упражнение 21Найдите объем куба, вписанного в единичный октаэдр.
- 26. Упражнение 22Найдите объем куба, описанного около единичного октаэдра.
- 27. Упражнение 23Найдите объем куба, вписанного в единичный додекаэдр.
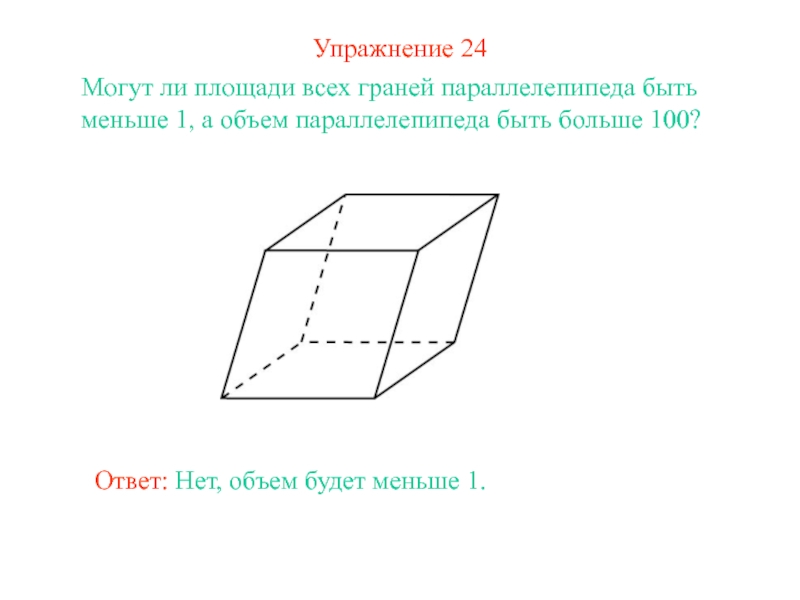
- 28. Упражнение 24Могут ли площади всех граней параллелепипеда
- 29. Упражнение 25Могут ли площади всех граней параллелепипеда
- 30. Упражнение 26Сколько имеется плоскостей, делящих параллелепипед на две равновеликие части?Ответ: Бесконечно много.
- 31. Упражнение 27Четыре грани параллелепипеда – прямоугольники со
- 32. Упражнение 28Какой наибольший объем может иметь параллелепипед,
- 33. Упражнение 29Какой наибольший объем может иметь параллелепипед,
- 34. Упражнение 30Какой наибольший объем может иметь параллелепипед, вписанный в сферу радиуса 1?
- 35. Скачать презентанцию
ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 1Объем наклонного параллелепипеда равен произведению площади S грани параллелепипеда на высоту h, проведенную к этой грани, т.е. имеет место формула
Слайды и текст этой презентации
Слайд 1ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА
Объем прямоугольного параллелепипеда равен произведению трех его измерений,
т.е. имеет место формула
выходящие из одной вершины.
Слайд 2ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 1
Объем наклонного параллелепипеда равен произведению площади S
грани параллелепипеда на высоту h, проведенную к этой грани, т.е.
имеет место формула
Слайд 3ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 2
Если ребро параллелепипеда равно c и образует
с гранью площади S угол , то объем
параллелепипеда вычисляется по формуле
Слайд 4ОБЪЕМ НАКЛОННОГО ПАРАЛЛЕЛЕПИПЕДА 3
Пусть ребра параллелепипеда, выходящие из одной вершины,
равны a, b, c. Ребра a и b образуют угол
, а ребро c наклонено к плоскости ребер a и b под углом Тогда объем V параллелепипеда выражается формулой
Слайд 5Упражнение 1
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1,
2, 3. Найдите объем параллелепипеда.
Ответ: 6.
Слайд 6Упражнение 2
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
1, 2. Объем параллелепипеда равен 3. Найдите третье ребро параллелепипеда,
выходящее из той же вершины.
Слайд 7Упражнение 3
Площадь грани прямоугольного параллелепипеда равна 2. Ребро, перпендикулярное этой
грани, равно 3. Найдите объем параллелепипеда.
Ответ: 6.
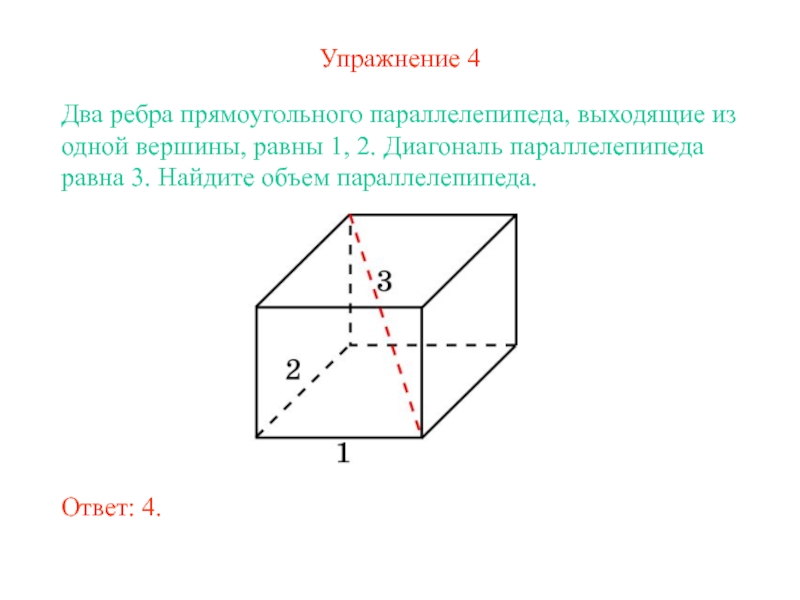
Слайд 8Упражнение 4
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
1, 2. Диагональ параллелепипеда равна 3. Найдите объем параллелепипеда.
Ответ: 4.
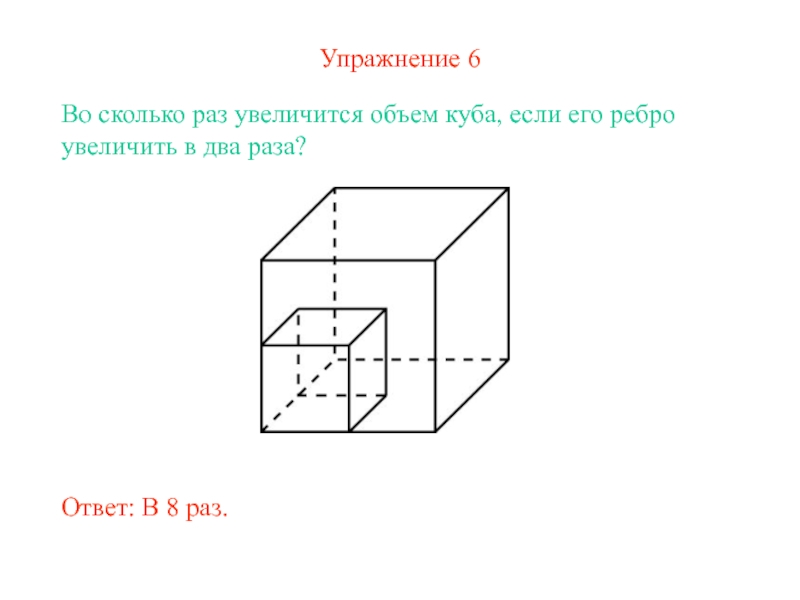
Слайд 10Упражнение 6
Во сколько раз увеличится объем куба, если его ребро
увеличить в два раза?
Ответ: В 8 раз.
Слайд 12Упражнение 8
Если каждое ребро куба увеличить на 2 см, то
его объем увеличится на 98 см2. Найдите ребро куба.
Ответ: 3.
Решение.
Пусть ребро куба равно x. Тогда Решая это уравнение, получим
Слайд 13Упражнение 9
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны
1, 2. Площадь поверхности параллелепипеда равна 10. Найдите объем параллелепипеда.
Слайд 14Упражнение 10
Ребро прямоугольного параллелепипеда равно 1. Диагональ равна 3. Площадь
поверхности параллелепипеда равна 16. Найдите объем параллелепипеда.
Слайд 15Упражнение 11
Диагональ прямоугольного параллелепипеда равна 1 и образует углы 30о,
45о и 60о с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
Слайд 16Упражнение 12
Площади трех граней параллелепипеда равны 1, 2, 3. Найдите
объем параллелепипеда.
Слайд 17Упражнение 13
Две противоположные грани параллелепипеда – квадраты со стороной 1.
Соединяющее их ребро равно 1 и наклонено к плоскостям этих
граней под углом 60о. Найдите объем параллелепипеда.
Слайд 18Упражнение 14
Гранью параллелепипеда является ромб со стороной 1 и острым
углом 60о. Одно из ребер параллелепипеда перпендикулярно этой грани и
равно 1. Найдите объем параллелепипеда.
Слайд 19Упражнение 15
Гранью параллелепипеда является ромб со стороной 1 и острым
углом 60о. Одно из ребер параллелепипеда составляет с этой гранью
угол 60о и равно 1. Найдите объем параллелепипеда.
Слайд 20Упражнение 16
Три грани параллелепипеда, имеющие общую вершину, являются ромбами со
сторонами 1 и острыми углами при этой вершине 60о. Найдите
объем параллелепипеда.
Слайд 21Упражнение 17
В параллелепипеде две грани имеют площади S1 и S2,
их общее ребро равно a, и они образуют между собой
двугранный угол 150о. Найдите объем параллелепипеда.
Слайд 22Упражнение 18
В параллелепипеде две грани являются прямоугольниками с площадями 20
см2 и 24 см2. Угол между их плоскостями равен 30о.
Еще одна грань этого параллелепипеда имеет площадь 15 см2. Найдите объем параллелепипеда.
Слайд 23Упражнение 19
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота
которого равны 1. Найдите объем параллелепипеда.
Решение: Ребра параллелепипеда равны 2,
2 и 1. Его объем равен 4.
Слайд 28Упражнение 24
Могут ли площади всех граней параллелепипеда быть меньше 1,
а объем параллелепипеда быть больше 100?
Ответ: Нет, объем будет меньше
1.
Слайд 29Упражнение 25
Могут ли площади всех граней параллелепипеда быть больше 100,
а объем параллелепипеда быть меньше 1?
Ответ: Да.
Слайд 30Упражнение 26
Сколько имеется плоскостей, делящих параллелепипед на две равновеликие части?
Ответ:
Бесконечно много.
Слайд 31Упражнение 27
Четыре грани параллелепипеда – прямоугольники со сторонами 1 и
2. Какой наибольший объем может иметь этот параллелепипед?
Слайд 32Упражнение 28
Какой наибольший объем может иметь параллелепипед, вписанный в прямой
цилиндр, радиус основания и высота которого равны 1?
Слайд 33Упражнение 29
Какой наибольший объем может иметь параллелепипед, сумма длин ребер
которого, выходящих из одной вершины, равна 1?
Слайд 34Упражнение 30
Какой наибольший объем может иметь параллелепипед, вписанный в сферу
радиуса 1?
