Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИКА Готовимся к Всероссийской проверочной работе 6 КЛАСС
Содержание
- 1. МАТЕМАТИКА Готовимся к Всероссийской проверочной работе 6 КЛАСС
- 2. Время выполнения работы – 60 минут.Работа содержит 13 заданий.Готовимся к Всероссийской проверочной работе6 КЛАСС
- 3. Нельзя пользоваться учебниками, справочниками, калькулятором.Можно пользоваться черновиком.
- 4. Готовимся к Всероссийской проверочной работе6 КЛАССРабота содержит
- 5. Готовимся к Всероссийской проверочной работе6 КЛАСССВОЙСТВА АРИФМЕТИЧЕСКИХ
- 6. Готовимся к Всероссийской проверочной работе6 КЛАСССВОЙСТВА АРИФМЕТИЧЕСКИХ
- 7. Готовимся к Всероссийской проверочной работе6 КЛАСССВОЙСТВА АРИФМЕТИЧЕСКИХ
- 8. Готовимся к Всероссийской проверочной работе6 КЛАСССВОЙСТВА АРИФМЕТИЧЕСКИХ
- 9. Готовимся к Всероссийской проверочной работе6 КЛАСССВОЙСТВА АРИФМЕТИЧЕСКИХ
- 10. Готовимся к Всероссийской проверочной работе6 КЛАССВЫПОЛНЕНИЕ ДЕЙСТВИЙ
- 11. Готовимся к Всероссийской проверочной работе6 КЛАССНАХОЖДЕНИЕ НЕИЗВЕСТНОГО
- 12. Готовимся к Всероссийской проверочной работе6 КЛАССНАХОЖДЕНИЕ НЕИЗВЕСТНОГО
- 13. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 14. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 15. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИИз
- 16. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 17. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 18. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 19. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 20. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 21. Готовимся к Всероссийской проверочной работе6 КЛАССОБЫКНОВЕННЫЕ ДРОБИ
- 22. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 23. Готовимся к Всероссийской проверочной работе6 КЛАССДЕСЯТИЧНЫЕ ДРОБИЧтобы
- 24. Готовимся к Всероссийской проверочной работе6 КЛАССДЕСЯТИЧНЫЕ ДРОБИ
- 25. Готовимся к Всероссийской проверочной работе6 КЛАССОКРУГЛЕНИЕ ДЕСЯТИЧНЫХ
- 26. Готовимся к Всероссийской проверочной работе6 КЛАССДЕСЯТИЧНЫЕ ДРОБИЧтобы
- 27. Готовимся к Всероссийской проверочной работе6 КЛАССДЕСЯТИЧНЫЕ ДРОБИЧтобы
- 28. Готовимся к Всероссийской проверочной работе6 КЛАССДЕСЯТИЧНЫЕ ДРОБИЧтобы
- 29. Готовимся к Всероссийской проверочной работе6 КЛАСССРЕДНЕЕ АРИФМЕТИЧЕСКОЕЧтобы
- 30. Готовимся к Всероссийской проверочной работе6 КЛАССНАХОЖДЕНИЕ ЧАСТИ
- 31. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 32. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 33. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 34. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 35. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 36. Готовимся к Всероссийской проверочной работе6 КЛАСС
- 37. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 38. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 39. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 40. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 41. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 42. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 43. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 44. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 45. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 46. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 47. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 48. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 49. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 50. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 51. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 52. Готовимся к Всероссийской проверочной работе6 КЛАССЧерняева М.
- 53. МАТЕМАТИКАЧерняева М. А., Доброхвалов Р. А. Всероссийские проверочные работы. Математика. 15 типовых вариантов. 6 КЛАСС.6 КЛАСС
- 54. МАТЕМАТИКАhttps://prosv.ru/
- 55. МАТЕМАТИКА
- 56. Скачать презентанцию
Время выполнения работы – 60 минут.Работа содержит 13 заданий.Готовимся к Всероссийской проверочной работе6 КЛАСС
Слайды и текст этой презентации
Слайд 2
Время выполнения работы – 60 минут.
Работа содержит 13 заданий.
Готовимся к
Всероссийской проверочной работе
Слайд 3Нельзя пользоваться учебниками, справочниками, калькулятором.
Можно пользоваться черновиком.
Записи в черновике
проверяться
и оцениваться не будут.
Готовимся к Всероссийской проверочной работе
6 КЛАСС
Слайд 4Готовимся к Всероссийской проверочной работе
6 КЛАСС
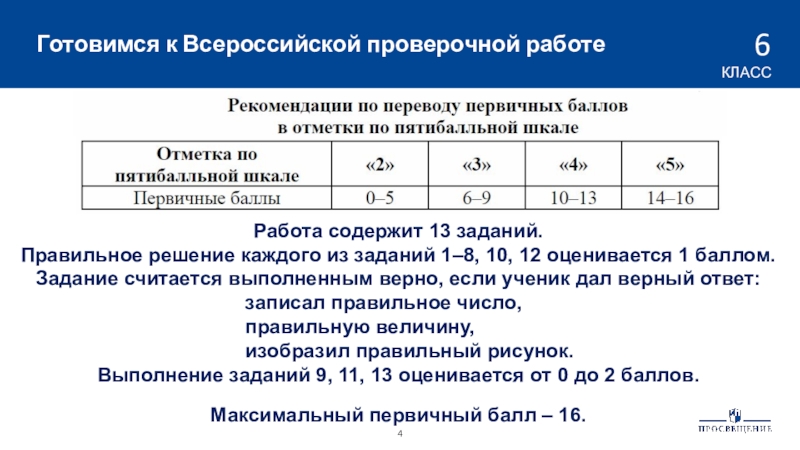
Работа содержит 13 заданий.
Правильное решение
каждого из заданий 1–8, 10, 12 оценивается 1 баллом.
Задание
считается выполненным верно, если ученик дал верный ответ: записал правильное число,
правильную величину,
изобразил правильный рисунок.
Выполнение заданий 9, 11, 13 оценивается от 0 до 2 баллов.
Максимальный первичный балл – 16.
Слайд 5Готовимся к Всероссийской проверочной работе
6 КЛАСС
СВОЙСТВА АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы умножить число
на произведение двух чисел,
можно сначала умножить его на первый
множитель, а потом полученное произведение
умножить на второй множитель
(сочетательное свойство умножения).
ПРИМЕР. Найдите значение выражения 25 · (4 · 16).
Решение. 25 · (4 · 16) = (25 · 4) · 16 = 100 · 16 = 1600.
Слайд 6Готовимся к Всероссийской проверочной работе
6 КЛАСС
СВОЙСТВА АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы вычесть сумму
из числа, можно вначале вычесть из этого
числа первое слагаемое, а
потом из полученной разности вычесть второе слагаемое.ПРИМЕР. Найдите значение выражения 94 – (4 + 29).
Решение. 94 – (4 + 29) = (94 – 4) – 29 = 90 – 29 = 61.
Слайд 7Готовимся к Всероссийской проверочной работе
6 КЛАСС
СВОЙСТВА АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы из суммы
вычесть число, можно вычесть его из одного слагаемого, а к
полученной разности прибавить оставшееся слагаемое.ПРИМЕР. Найдите значение выражения (86 + 34) – 26.
Решение. (86 + 34) – 26 = (86 – 26) + 34 = 60 + 34 = 94.
Слайд 8Готовимся к Всероссийской проверочной работе
6 КЛАСС
СВОЙСТВА АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы умножить сумму
на число, можно умножить на это число
каждое слагаемое и сложить
получившиеся произведения (распределительное свойство умножения относительно сложения).ПРИМЕР. Найдите значение выражения (54 + 15) · 2.
Решение. (54 + 15) · 2 = (54 · 2) + (15 · 2) = 108 + 30 = 138.
Слайд 9Готовимся к Всероссийской проверочной работе
6 КЛАСС
СВОЙСТВА АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы умножить разность
на число, можно умножить уменьшаемое
и вычитаемое на это число и
из первого произведения вычесть второе(распределительное свойство умножения относительно вычитания).
ПРИМЕР. Найдите значение выражения (33 – 25) · 4.
Решение. (33 – 25) · 4 = (33 · 4) – (25 · 4) = 132 – 100 = 32.
Слайд 10Готовимся к Всероссийской проверочной работе
6 КЛАСС
ВЫПОЛНЕНИЕ ДЕЙСТВИЙ В ЧИСЛОВОМ ВЫРАЖЕНИИ
1)
Если в выражении нет скобок и оно содержит действия только
одной ступени (сложение и вычитание или умножение и деление), то их выполняют по порядку слева направо.2) Если выражение содержит действия первой (сложение и вычитание) и второй (умножение и деление) ступени и в нём нет скобок, то сначала выполняют действия второй ступени, а потом — действия первой ступени.
3) Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2).
Слайд 11Готовимся к Всероссийской проверочной работе
6 КЛАСС
НАХОЖДЕНИЕ НЕИЗВЕСТНОГО КОМПОНЕНТА
АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы найти
неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
ПРИМЕР. Найдите неизвестное,
записанное буквой x, в выражении x + 154 = 247.Решение. x + 154 = 247, x = 247 – 154, x = 93.
Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.
ПРИМЕР. Найдите неизвестное, записанное буквой x, в выражении x – 168 = 321.
Решение. x – 168 = 321, x = 168 + 321, x = 489.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
ПРИМЕР. Найдите неизвестное, записанное буквой x, в выражении 149 – x = 83.
Решение. 149 – x = 83, x = 149 – 83, x = 66.
Слайд 12Готовимся к Всероссийской проверочной работе
6 КЛАСС
НАХОЖДЕНИЕ НЕИЗВЕСТНОГО КОМПОНЕНТА
АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
Чтобы найти
неизвестный множитель, надо произведение разделить на известный множитель.
ПРИМЕР. Найдите неизвестное,
записанное буквой x, в выражении 37 · x = 148.Решение. 37 · x = 148, x = 148 : 37, x = 4.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
ПРИМЕР. Найдите неизвестное, записанное буквой x, в выражении x : 6 = 48.
Решение. x : 6 = 48, x = 6 · 48, x = 288.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
ПРИМЕР. Найдите неизвестное, записанное буквой а, в выражении 369 : x = 123.
Решение. 369 : x = 123, x = 369 : 123, x = 3.
Слайд 15Готовимся к Всероссийской проверочной работе
6 КЛАСС
ОБЫКНОВЕННЫЕ ДРОБИ
Из двух дробей с
одинаковыми знаменателями больше та дробь, у которой больше числитель.
Слайд 23Готовимся к Всероссийской проверочной работе
6 КЛАСС
ДЕСЯТИЧНЫЕ ДРОБИ
Чтобы сложить (вычесть) десятичные
дроби, нужно:
1) уравнять в этих дробях количество знаков после запятой;
2)
записать их друг под другом так, чтобы запятая была записана под запятой;3) выполнить сложение (вычитание), не обращая внимания на запятую;
4) поставить в ответе запятую под запятой в данных дробях.
Слайд 25Готовимся к Всероссийской проверочной работе
6 КЛАСС
ОКРУГЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
1) Если первая
отброшенная или заменённая нулём цифра равна 5, 6, 7, 8,
9, то стоящую перед ней цифру увеличивают на 1.2) Если первая отброшенная или заменённая нулём цифра равна 0, 1, 2, 3, 4, то стоящую перед ней цифру оставляют без изменения.
ПРИМЕР. Округлите:
1) 251,73 до десятых;
2) 4,547 до сотых;
Решение.
1) 251,73 ≈ 251,7;
2) 4,547 ≈ 4,55;
Слайд 26Готовимся к Всероссийской проверочной работе
6 КЛАСС
ДЕСЯТИЧНЫЕ ДРОБИ
Чтобы умножить десятичную дробь
на натуральное число, надо:
1) умножить её на это число, не
обращая внимания на запятую;2) в полученном произведении отделить запятой столько цифр справа,
сколько их отделено запятой в десятичной дроби.
ПРИМЕР. Найдите значение выражения 2,34 · 13.
Слайд 27Готовимся к Всероссийской проверочной работе
6 КЛАСС
ДЕСЯТИЧНЫЕ ДРОБИ
Чтобы разделить десятичную дробь
на натуральное число, надо:
1) разделить дробь на это число, не
обращая внимания на запятую;2) поставить в частном запятую, когда кончится деление целой части.
ПРИМЕР. Найдите значение выражения 662,4 : 36.
Решение. 662,4 : 36 = 18,4.
Слайд 28Готовимся к Всероссийской проверочной работе
6 КЛАСС
ДЕСЯТИЧНЫЕ ДРОБИ
Чтобы разделить десятичную дробь
на натуральное число, надо:
1) разделить дробь на это число, не
обращая внимания на запятую;2) поставить в частном запятую, когда кончится деление целой части.
ПРИМЕР. Найдите значение выражения 662,4 : 36.
Решение. 662,4 : 36 = 18,4.
Чтобы разделить число на десятичную дробь, надо:
1) в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
2) после этого выполнить деление на натуральное число.
ПРИМЕР. Найдите значение выражения 10 872 : 3,6.
Решение. 10 872 : 3,6 = 108 720 : 36 = 3020.
Слайд 29Готовимся к Всероссийской проверочной работе
6 КЛАСС
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
Чтобы найти среднее арифметическое
нескольких чисел, надо:
1) найти сумму этих чисел;
2) разделить полученную сумму
на число слагаемых.ПРИМЕР. Найдите среднее арифметическое чисел 12, 19, 11, 24, 73 и 65.
Слайд 30Готовимся к Всероссийской проверочной работе
6 КЛАСС
НАХОЖДЕНИЕ ЧАСТИ ОТ ЧИСЛА
Чтобы найти
дробь от числа, надо умножить число на эту дробь.
ПРИМЕР. Найдите
треть от 90.Слайд 37Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6№ 13. На доске было написано двузначное число. Саша переставил цифры, и полученное число увеличилось в 1,75 раза. Какое двузначное число было записано первоначально?
Слайд 38Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6№ 13. На доске было написано двузначное число. Саша переставил цифры, и полученное число увеличилось в 1,75 раза. Какое двузначное число было записано первоначально?
Решение.
Запись любого двузначного числа: 10a + b, где a цифра десятков, а b цифра единиц.
Если цифры переставить, как это сделал Саша, то получится новое число:
10b+a, которое по условию больше написанного на доске в 1,75 раз.
Слайд 39Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6№ 13. На доске было написано двузначное число. Саша переставил цифры, и полученное число увеличилось в 1,75 раза. Какое двузначное число было записано первоначально?
Решение.
Запись любого двузначного числа: 10a + b, где a цифра десятков, а b цифра единиц.
Если цифры переставить, как это сделал Саша, то получится новое число:
10b+a, которое по условию больше написанного на доске в 1,75 раз.
Составим уравнение:
1,75(10a + b) = 10b + a;
17,5a + 1,75b = 10b + a;
16,5a = 8,25b.
Слайд 40Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6№ 13. На доске было написано двузначное число. Саша переставил цифры, и полученное число увеличилось в 1,75 раза. Какое двузначное число было записано первоначально?
Решение.
Запись любого двузначного числа: 10a + b, где a цифра десятков, а b цифра единиц.
Если цифры переставить, как это сделал Саша, то получится новое число:
10b+a, которое по условию больше написанного на доске в 1,75 раз.
Составим уравнение:
1,75(10a + b) = 10b + a;
17,5a + 1,75b = 10b + a;
16,5a = 8,25b. Умножим обе части уравнения на 100, получим:
1650a = 825b
Слайд 41Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6№ 13. На доске было написано двузначное число. Саша переставил цифры, и полученное число увеличилось в 1,75 раза. Какое двузначное число было записано первоначально?
Решение.
Запись любого двузначного числа: 10a + b, где a цифра десятков, а b цифра единиц.
Если цифры переставить, как это сделал Саша, то получится новое число:
10b+a, которое по условию больше написанного на доске в 1,75 раз.
Составим уравнение:
1,75(10a + b) = 10b + a;
17,5a + 1,75b = 10b + a;
16,5a = 8,25b. Умножим обе части уравнения на 100, получим:
1650a = 825b. Разделим обе части уравнения на 825, получим:
2a = b. То есть цифра единиц написанного на доске числа в два раза больше цифры десятков. Этому условию соответствую двузначные числа 12; 24; 36 и 48.
Ответ: 12; 24; 36 и 48.
Слайд 42Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
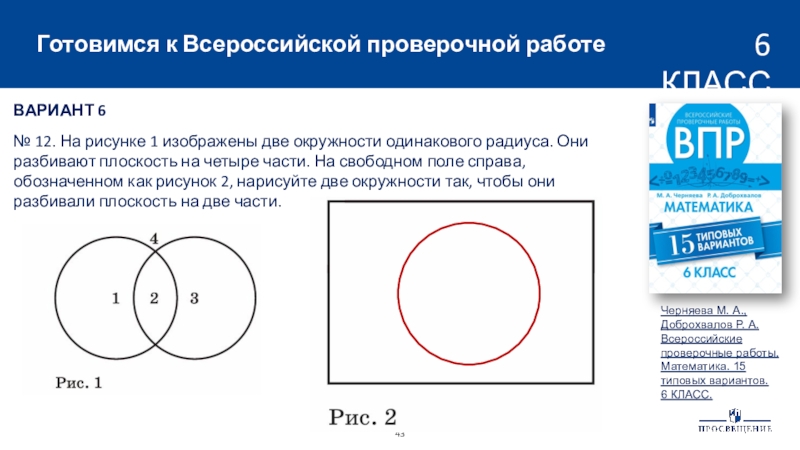
6№ 12. На рисунке 1 изображены две окружности одинакового радиуса. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рисунок 2, нарисуйте две окружности так, чтобы они разбивали плоскость на две части.
Слайд 43Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
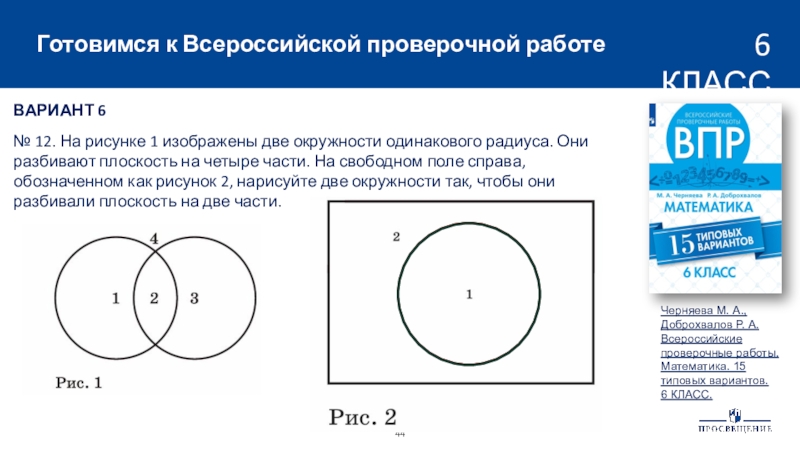
6№ 12. На рисунке 1 изображены две окружности одинакового радиуса. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рисунок 2, нарисуйте две окружности так, чтобы они разбивали плоскость на две части.
Слайд 44Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6№ 12. На рисунке 1 изображены две окружности одинакового радиуса. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рисунок 2, нарисуйте две окружности так, чтобы они разбивали плоскость на две части.
Слайд 45Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6Слайд 46Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6Слайд 47Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6Слайд 48Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6Слайд 49Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6Слайд 50Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
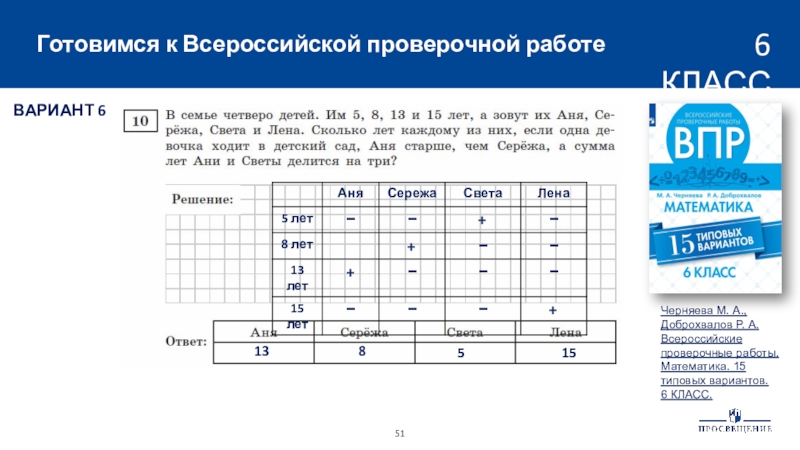
6Слайд 51Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
65
15
8
13
Слайд 52Готовимся к Всероссийской проверочной работе
6 КЛАСС
Черняева М. А., Доброхвалов Р.
А. Всероссийские проверочные работы. Математика. 15 типовых вариантов.
6 КЛАСС.
ВАРИАНТ
6Весь путь 100 %.
100% - 15% - 55% = 30% - путь, пройденный по лесу.
56 ∙ 0,3 = 16,8 (км)
16,8 км