Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Механическое равновесие, механические колебания и волны Сила Архимеда, закон
Содержание
- 1. Механическое равновесие, механические колебания и волны Сила Архимеда, закон
- 2. 4.2.1 Диапазон голоса мужского баса занимает частотный
- 3. 4.2.2 На рисунке изображён участок натянутого резинового
- 4. Механическое равновесие, механические колебания и волныСила Архимеда, закон ПаскаляВолныПружинный и математический маятники, колебанияМеханическое равновесие
- 5. 4.3.1. Период колебаний потенциальной энергии горизонтального пружинного
- 6. 4.3.2. На рисунке представлен график зависимости потенциальной
- 7. 4.3.3. На рисунке изображена зависимость амплитуды установившихся
- 8. 4.3.4. На графиках представлена зависимость координаты х
- 9. 4.3.5. Груз на длинной лёгкой пружине совершает
- 10. 4.3.6. Груз, закреплённый на лёгкой пружине жёсткостью
- 11. Скачать презентанцию
4.2.1 Диапазон голоса мужского баса занимает частотный интервал от до Каково отношение граничных длин звуковых волн этого интервала?Частота, длина и скорость распространения звуковых волн связаны соотношением
Слайды и текст этой презентации
Слайд 1Механическое равновесие, механические колебания и волны
Сила Архимеда, закон Паскаля
Волны
Пружинный и
математический маятники, колебания
Слайд 24.2.1 Диапазон голоса мужского баса занимает частотный интервал от до
Каково отношение граничных длин звуковых волн этого интервала?
Частота, длина и
скорость распространения звуковых волн связаны соотношением 
Слайд 34.2.2 На рисунке изображён участок натянутого резинового шнура, по которому
распространяется поперечная волна, имеющая частоту 1,6 Гц. Чему равна скорость
распространения волны? (Ответ дайте в метрах в секунду.)Скорость распространения волны связана с частотой и длиной волны соотношением
Из рисунка видно, что 20 см составляют 1/4 длины волны, следовательно:
Слайд 4Механическое равновесие, механические колебания и волны
Сила Архимеда, закон Паскаля
Волны
Пружинный и
математический маятники, колебания
Механическое равновесие
Слайд 54.3.1. Период колебаний потенциальной энергии горизонтального пружинного маятника 1 с. Каким
будет период ее колебаний, если массу груза маятника увеличить в
2 раза, а жесткость пружины вдвое уменьшить? (Ответ дайте в секундах.)Период колебаний потенциальной энергии пружинного маятника
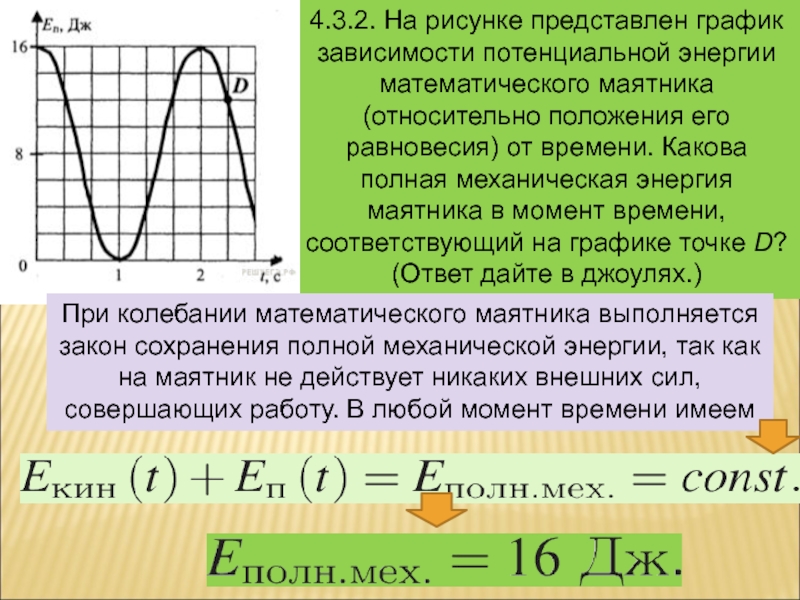
Слайд 64.3.2. На рисунке представлен график зависимости потенциальной энергии математического маятника
(относительно положения его равновесия) от времени. Какова полная механическая энергия
маятника в момент времени, соответствующий на графике точке D? (Ответ дайте в джоулях.)При колебании математического маятника выполняется закон сохранения полной механической энергии, так как на маятник не действует никаких внешних сил, совершающих работу. В любой момент времени имеем
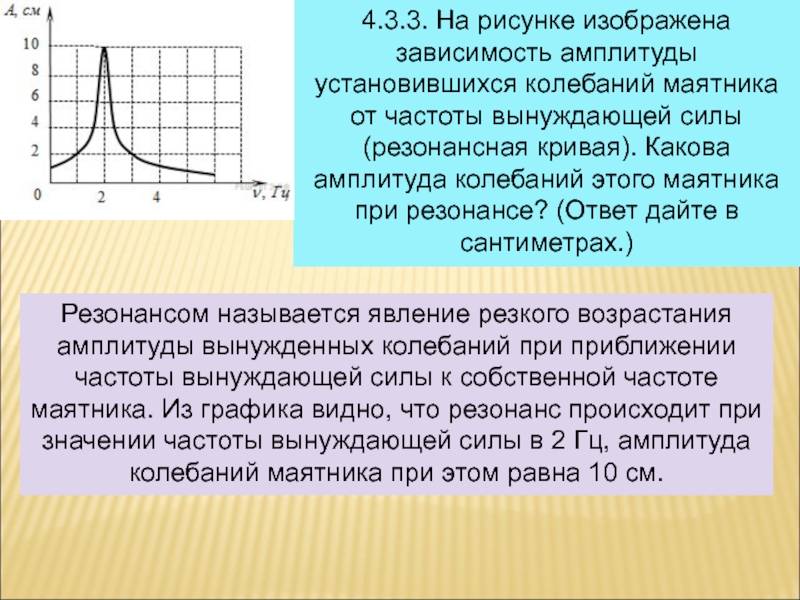
Слайд 74.3.3. На рисунке изображена зависимость амплитуды установившихся колебаний маятника от
частоты вынуждающей силы (резонансная кривая). Какова амплитуда колебаний этого маятника
при резонансе? (Ответ дайте в сантиметрах.)Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте маятника. Из графика видно, что резонанс происходит при значении частоты вынуждающей силы в 2 Гц, амплитуда колебаний маятника при этом равна 10 см.
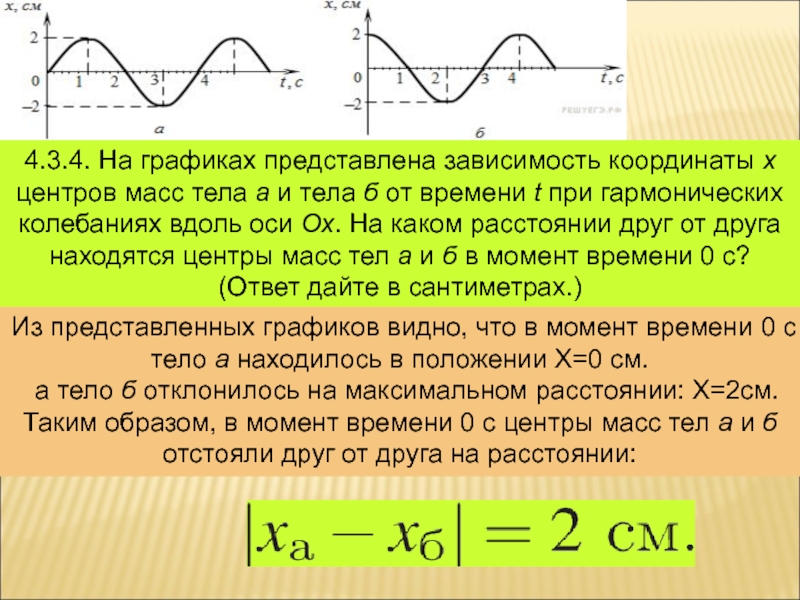
Слайд 84.3.4. На графиках представлена зависимость координаты х центров масс тела
а и тела б от времени t при гармонических колебаниях
вдоль оси Ox. На каком расстоянии друг от друга находятся центры масс тел а и б в момент времени 0 с? (Ответ дайте в сантиметрах.)Из представленных графиков видно, что в момент времени 0 с тело а находилось в положении Х=0 см.
а тело б отклонилось на максимальном расстоянии: Х=2см. Таким образом, в момент времени 0 с центры масс тел а и б отстояли друг от друга на расстоянии:
Слайд 94.3.5. Груз на длинной лёгкой пружине совершает колебания с частотой
0,5 Гц. Пружину разрезали на 4 равные части и прикрепили
к одной из частей тот же груз. Чему стал равен период колебаний получившегося пружинного маятника? (Ответ дайте в секундах.)При последовательном соединении пружин, общая жёсткость получается из формулы:
Отсюда следует, что жёсткость 1/4 части исходной пружины равна 4k.
Увеличение жёсткости пружины в 4 раза приводит к уменьшению периода колебаний в два раза, а частота, являясь обратной периоду величиной, в свою очередь должна увеличиться в два раза и станет равной 1 Гц. Тогда период колебаний получившегося маятника будет равен 1 с.
Слайд 104.3.6. Груз, закреплённый на лёгкой пружине жёсткостью 200 Н/м, совершает
вертикальные колебания. На рисунке изображены графики зависимости смещения x груза
от времени t и проекции Vx скорости груза от времени. Определите, чему равна масса груза. Ответ выразите в кг.При колебаниях кинетическая энергия груза переходит в потенциальную энергию пружины и обратно.
