Слайд 2ЭКСПЕРТИЗА В УПРАВЛЕНИИ
Роль экспертов в управлении:
Основные трудности, связанные с информацией,
возникающие при выработке сложных решений:
Исходная статистическая информация зачастую бывает
недостаточно достоверной.
Некоторая часть информации имеет качественный характер и не поддается количественной оценке.
В процессе подготовки решений часто возникают ситуации, когда в принципе необходимую информацию получить можно, однако в момент принятия решения она отсутствует, поскольку это связано с большими затратами времени или средств.
Существует большая группа факторов, которые могут повлиять на реализацию решения в будущем, но их нельзя точно предсказать.
любая научная или техническая идея содержит в себе потенциальную возможность различных схем ее реализации, а любое экономическое действие может приводить к многочисленным исходам.
В-шестых, при выборе наилучшего решения мы нередко сталкиваемся с многозначностью обобщенного критерия, на основе которого можно произвести сравнение возможных исходов.
Слайд 3Метод экспертных оценок
Сущность метода экспертных оценок заключается в проведении экспертами
интуитивно-логического анализа проблемы с количественной оценкой суждений и формальной обработкой
результатов. Получаемое в результате обработки обобщенное мнение экспертов принимается как решение проблемы.
Слайд 4В процессе управления эксперты производят две основные функции:
формируют объекты (альтернативные
ситуации, цели, решения и т. п.)
производят измерение их характеристик (вероятности
свершения событий, коэффициенты значимости целей, предпочтения решений и т. п.)
Слайд 5Область применения метода экспертных оценок:
составление перечня возможных событий в различных
областях за определенный промежуток времени;
определение наиболее вероятных интервалов времени свершения
совокупности событий;
определение целей и задач управления с упорядочением их по степени важности;
определение альтернативных (вариантов решения задачи с оценкой их предпочтения;
альтернативное распределение ресурсов для решения задач с оценкой их предпочтительности;
альтернативные варианты принятия решений в определенной ситуации с оценкой их предпочтительности.
Слайд 6Разновидности метода экспертных оценок
анкетирование и интервьюирование
мозговой штурм
дискуссия
совещание
оперативная игра
сценарий
метод Дельфи
Слайд 7Организация экспертного оценивания
1) Подготовка и издание руководящего документа. Формулировка цели
и основных положений работы.
2) Назначение руководителя экспертизы
3) Формирование рабочей
группы (РГ)
4) Разработка организации и методики проведения опроса
5)Проведение опроса
6) Обработка результатов
Слайд 8Подбор экспертов
Формирование системы характеристик эксперта
Организация процедуры подбора экспертов
Составление списка возможных
экспертов
Выбор из них экспертной комиссии в соответствии с компетентностью кандидатов.
Слайд 9Опрос экспертов
Опрос – главный этап совместной работы группы управления и
экспертов. Основным содержанием опроса является:
постановка задачи и предъявление вопросов
экспертам
информационное обеспечение работы экспертов
выработка экспертами суждений, оценок, предложений
сбор результатов работы экспертов
Можно назвать три типа задач, которые решаются в процессе опроса:
оценка качественная или количественная заданных объектов
построение новых объектов
построение и оценка новых объектов
Слайд 10Фактор – это множество, состоящее, по крайней мере, из двух
элементов, отражающих различные уровни некоторых подлежащих рассмотрению величин.
Факторы могут
быть:
количественные и качественные
дискретные и непрерывные.
Формализация информации и шкалы сравнений
Слайд 11При использовании номинальных шкал исследуемые объекты можно опознавать и различать
на основе трех аксиом идентификации:
i либо есть j, либо есть
не j;
если i есть j, то j есть i;
если i есть j и j есть k, то i есть k.
Факторы в данном случае выступают как ассоциативные показатели, обладающие информацией, которая может быть формализована в виде бинарных оценок двух уровней: 1 (идентичен) или 0 (различен).
Номинальные шкалы
Слайд 12В случаях, когда исследуемые объекты можно в результате сравнения расположить
в определенной последовательности с учетом какого-либо существенного фактора (факторов), используются
порядковые шкалы.
Предположим, что необходимо расположить в определенной последовательности n объектов по какому-либо фактору (критерию). Представим это упорядочение в виде матрицы А где i, j = 1,2,…, n.
Слайд 13Величины устанавливают соотношения между объектами и могут быть определены следующим
образом :
Слайд 15Для формализации оценок, полученных от экспертов, часто используют интервальные шкалы.
При использовании таких шкал для этих целей можно брать почти
все обычные статистические меры. Исключением являются те меры, которые предполагают знание «истинно» нулевой точки шкалы, которая вводится здесь условно.
Интервальные шкалы предполагают возможность трансформации оценок, полученных на одной шкале, в оценки на другой шкале при помощи уравнения x’=ax+b
Слайд 16В ряде случаев при формализации экспертных оценок используется свойство аддитивности,
которое присуще только шкале отношений. Наличие аддитивности выражается следующими аксиомами
:
если j = a и i > 0, то i + j > a;
i + j = j + i;
если i = a и j = b, то i + j = a + b;
(i + j) + k = i + (j + k).
Слайд 17ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК
В зависимости от целей экспертного оценивания и выбранного
метода измерения при обработке результатов опроса возникают следующие основные задачи:
построение
обобщенной оценки объектов на основе индивидуальных оценок экспертов
построение обобщенной оценки на основе парного сравнения объектов каждым экспертом
определение относительных весов объектов
определение согласованности мнений экспертов
определение зависимостей между ранжировками
оценка надежности результатов обработки
Слайд 18Групповая оценка объектов
Пусть m экспертов произвели оценку n объектов по
l показателям. Результаты оценки представлены в виде величин , где
j – номер эксперта, i – номер объекта, h – номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжирования, то величины представляют собой ранги. Если оценка объектов выполнена методом непосредственной оценки или методом последовательного сравнения, то величины представляют собой числа из некоторого отрезка числовой оси, или баллы. Обработка результатов оценки существенно зависит от рассмотренных методов измерения.
Слайд 21Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, т. е.
по результатам оценки объектов. Основной идеей этого вычисления является предположение
о том, что компетентность экспертов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов.
Слайд 24Рассмотрим теперь случай, когда эксперты производят оценку множества объектов методом
ранжирования так, что величины xij есть ранги.
Ранжировку можно представить
в виде матрицы парных сравнений, элементы которой определим следующим образом:
Слайд 29При ранжировании объектов эксперты обычно расходятся во мнениях по решаемой
проблеме. В связи с этим возникает необходимость количественной оценки степени
согласия экспертов. Получение количественной меры согласованности мнений экспертов позволяет более обоснованно интерпретировать причины в расхождении мнений.
В настоящее время известны две меры согласованности мнений группы экспертов: дисперсионный и энтропийный коэффициенты конкордации.
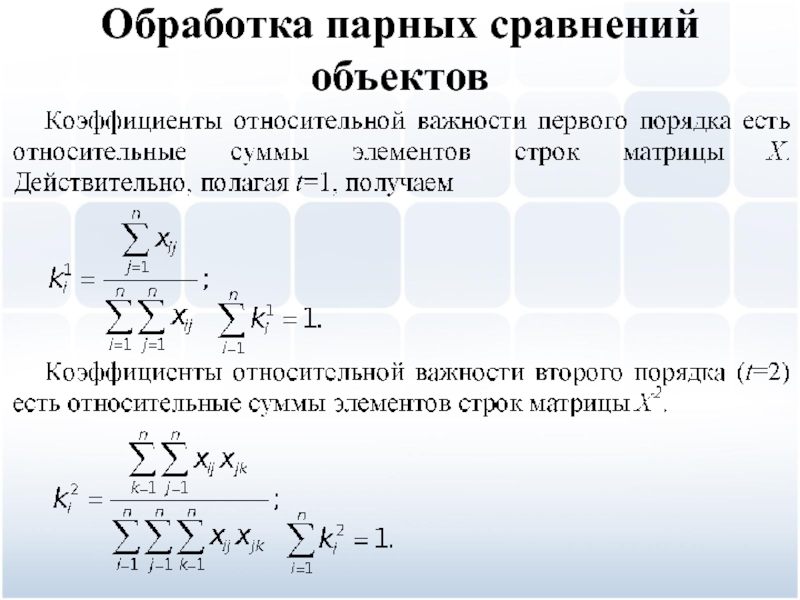
Слайд 34Обработка парных сравнений объектов
Слайд 35Обработка парных сравнений объектов
Слайд 36Обработка парных сравнений объектов
Слайд 37Обработка парных сравнений объектов
Слайд 43Определение взаимосвязи ранжировок
При обработке результатов ранжирования могут возникнуть задачи определения
зависимости между ранжировками двух экспертов, связи между достижением двух различных
целей при решении одной и той же совокупности проблем или взаимосвязи между двумя признаками.
В этих случаях мерой взаимосвязи может служить коэффициент ранговой корреляции. Характеристикой взаимосвязи множества ранжировок или целей будет являться матрица коэффициентов ранговой корреляции. Известны коэффициенты ранговой корреляции Спирмена и Кендалла.
Слайд 46Оценки средних рангов
Оценки средних рангов определяются формулами:
Слайд 47Вычислим оценки средних рангов и дисперсий в предположении, что в
ранжировках отсутствуют связанные ранги, т. е. обе ранжировки дают строгое
упорядочение объектов.
Две ранжировки могут отличаться друг от друга только перестановкой рангов, но сумма натуральных чисел и их квадратов не зависит от порядка (перестановки) слагаемых.
Слайд 48Дисперсии для двух любых ранжировок (при отсутствии связанных рангов) будут
одинаковы и равны
Дисперсии для двух любых ранжировок (при отсутствии
связанных рангов) будут одинаковы и равны
Слайд 49Для проведения практических расчетов удобнее пользоваться другой формулой
Первые две
суммы в правой части одинаковы и равны
Слайд 50Оценка коэффициента корреляцииявляется случайной величиной.
Слайд 53Сравнительная оценка коэффициентов ранговой корреляции Спирмена и Кендалла показывает, что
вычисление коэффициентов Спирмена производится по более простой формуле. Кроме того,
коэффициент Спирмена дает более точный результат, поскольку он является оптимальной по критерию минимума средней квадрата ошибки оценкой коэффициента корреляции.
Отсюда следует, что при практических расчетах корреляционной зависимости ранжировок предпочтительнее использовать коэффициент ранговой корреляции Спирмена.
Слайд 55ПРИМЕР:
Анализируя результаты работы экспертов, члены Правления фирмы были вынуждены констатировать,
что полного согласия между экспертами нет, а потому данные, приведенные
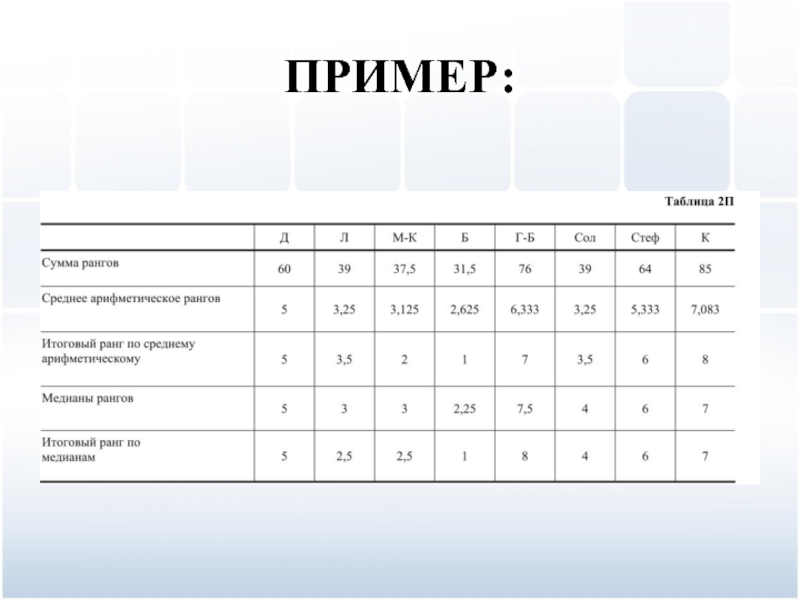
в табл. 1П, следует подвергнуть более тщательному математическому анализу. С этой целью был использован метод средних арифметических рангов. Для этого прежде всего была подсчитана сумма рангов, присвоенных проектам (табл. 1П). Затем эта сумма была разделена на число экспертов, в результате был рассчитан средний арифметический ранг. По средним рангам строится итоговая ранжировка (упорядочение), исходя из принципа – чем меньше средний ранг, тем лучше проект.
Слайд 56ПРИМЕР:
Результаты анализа показывают, что эксперт № 4 считает проекты М–К
и Б равноценными, они уступают лишь одному проекту – проекту
Сол. Поэтому проекты М–К и Б должны были бы стоять на втором и третьем местах и получить баллы 2 и 3. Поскольку они равноценны, то получают средний балл (2+3) / 2 = 5/ 2 = 2,5.
Наименьший средний ранг, равный 2,625, у проекта Б, следовательно, в итоговой ранжировке он получает ранг 1.
Следующая по величине сумма, равная 3,125, у проекта М–К. И он получает итоговый ранг 2. Проекты Л и Сол имеют одинаковые суммы (равные 3,25), значит, с точки зрения экспертов они равноценны (при рассматриваемом способе сведения вместе мнений экспертов с целью получения итоговой ранжировки), а потому они должны бы стоять на 3 и 4 местах и получают средний балл (3+4) /2 = 3,5. Дальнейшие результаты приведены в табл. 2П.
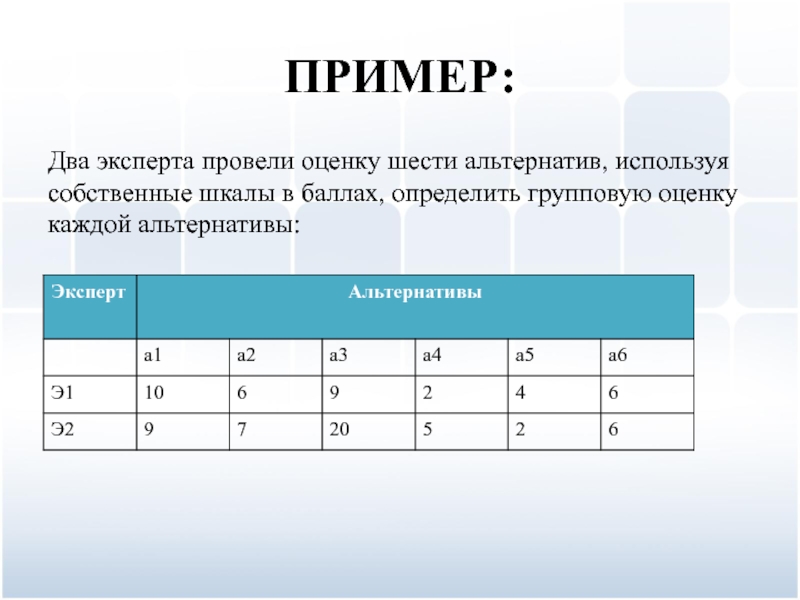
Слайд 58ПРИМЕР:
Два эксперта провели оценку шести альтернатив, используя собственные шкалы в
баллах, определить групповую оценку каждой альтернативы:
Слайд 59Установление степени согласованности мнений экспертов
В случае участия в опросе нескольких
экспертов расхождения в их оценках неизбежны, однако величина этого расхождения
имеет важное значение. Групповая оценка может считаться достаточно надежной только при условии хорошей согласованности ответов отдельных специалистов.
Для анализа разброса и согласованности оценок применяются статистические характеристики – методы разброса.
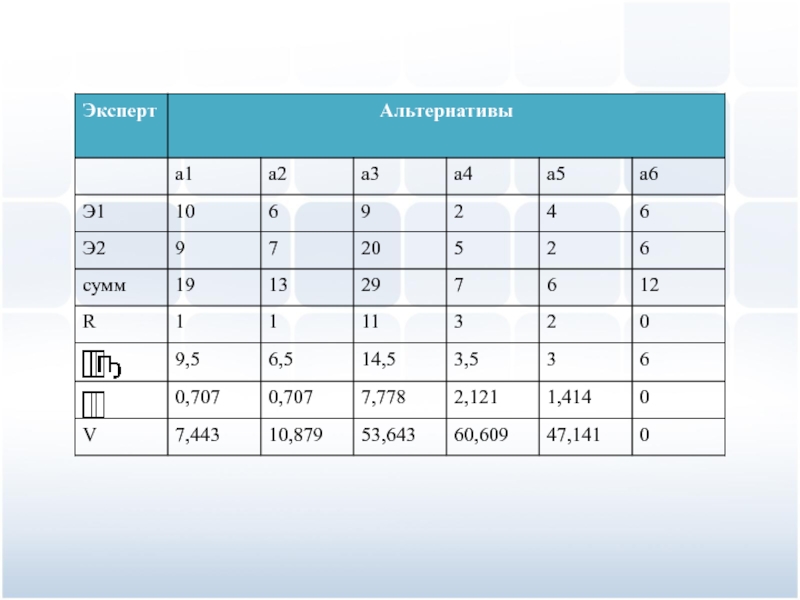
Слайд 60Вариационный размах:
Среднее квадратичное отклонение:
Коэффициент вариации:
Слайд 62Вычисление коэффициентов экспертов:
(см. слайд 22)
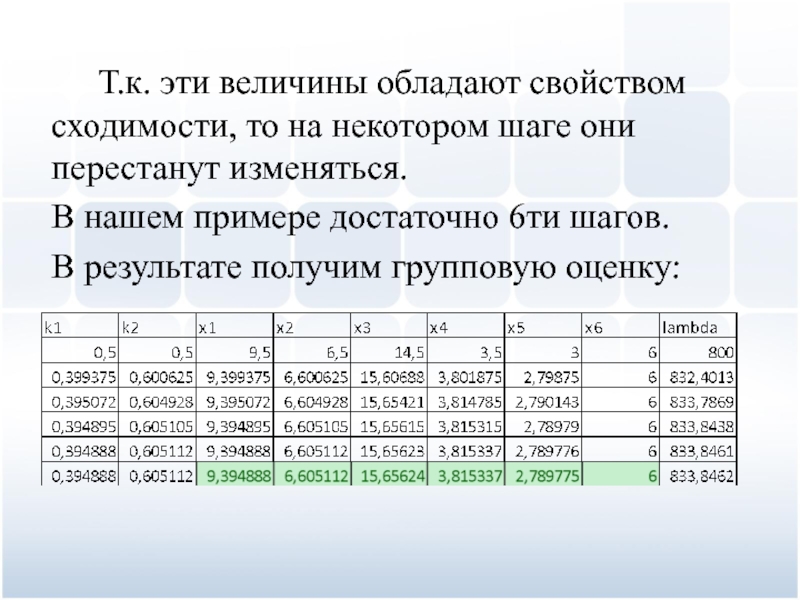
Слайд 64Т.к. эти величины обладают свойством сходимости, то на некотором шаге
они перестанут изменяться.
В нашем примере достаточно 6ти шагов.
В результате получим
групповую оценку: