Метод МО Хюккеля

и полезных вариантов общего метода МО ЛКАО.
Несколько приближений:
Каждая МО

i = С1  1 + С2  2 + . . . + Сn  n

n — число атомов

Полный набор МО:

оператора Фока
интегралы перекрывания для данной пары атомов
орбитальная энергия
В методе МОХ

МОХ относится к большой группе т.н. полуэмпирических вариантов общего метода МО.

интеграл)
(что все атомы, входящие в состав молекулы, одинаковы по своей

Третье приближение

недиагональные интегралы Fij

Пары атомов с хим. связями

Fij =  (т.н. резонансный интеграл)

Пары атомов без хим. связей

Fij = 0

Структура матрицы уравнений Рутана в методе Хюккеля определенным образом "приспосабливается" к топологии молекулы. Поэтому метод МОХ относится к классу т.н. топологических вариантов МО.

сделанных приближений
Система уравнений Рутана
разделим все элементы матрицы на число 

имеют решения только тогда, когда определитель системы равен нулю.
Раскрыв этот

При подстановке их в систему, получим n экземпляров системы, причем все они будут заведомо совместны (разрешимы).

Энергии соответствующих орбиталей легко рассчитать через значения корней: i =  –  • хi .

+ C1b pb
2 = С2а pa + C2b pb
Уравнения

характеристическое уравнение: х2 – 1 = 0

х1 = +1 и х2 = –1

С1a = (0,5)1/2 и C1b = – (0,5)1/2

С2a = (0,5)1/2 и C2b = (0,5)1/2

равны:
1 =  –  • х1

Корреляционная энергетическая диаграмма

Е = 2

Связывающая МО

Разрыхляющая МО

 ~ 65 кДж/моль (по частоте перехода молекулы в возбуждённое состояние)

высокой энергией имеет дополнительную узловую поверхность, относительно МО с меньшей

и Сb = – Cd
Поскольку поднаборы никак не связаны

них две линейно независимые и взаимно ортогональные МО, которые будут

Например, такой базис можно получить, если положить:

Возможны и другие варианты выбора базиса. Например, образуем еще один базис из предыдущего путем построения суммы и разности орбиталей ' и ''

+ = (0,5)1/2 [ ' + '' ] – = (0,5)1/2 [ ' – '' ]

+ = 0,5 ( pa + pb – pс – pd )  + = 
– = 0,5 ( pa – pb – pс + pd )  – = 

Ситуация аналогична модели плоского ротатора!

 + 2 до  – 2, располагаясь, по мере

энергетические зоны

полупроводниковые свойства

связывающие и разрыхляющие энергетические уровни располагаются симметрично, относительно атомного уровня (). Для нечетных полиенов (нечетное число атомов) наблюдается, кроме того, один несвязывающий уровень.

набор углов:
k = ( • k • ) /

Построим для каждого такого угла (угол нужно отсчитывать от горизонтальной оси) радиус-вектор в круге радиусом R = [2 / (n + 1)]1/2. Проекции этих векторов на вертикальную ось и дадут величины коэффициентов Сk

/5; 2/5; 3/5; 4/5 Коэффициенты:
{0,372 0,602 0,602

Молекулярная орбиталь:

Углы: : 2 = 2/5; 4/5; 6/5; 8/5. Коэффициенты :

{0,602 0,372 – 0,372 – 0,602}

k = 2

k = 1

Молекулярная орбиталь:

{0,602 – 0,372 – 0,372 0,602}.
Молекулярная орбиталь:
k

Углы: 4 = 4/5; 8/5; 12/5; 16/5 Коэффициенты:

{0,372 – 0,602 0,602 – 0,372}

Молекулярная орбиталь:

исключением самого нижнего у всех циклов и самого верхнего у

число связывающих МО

нечетное (2n + 1)

полная электронная емкость равна 2(2n + 1) = 4n + 2

Ароматической является плоская моноциклическая сопряженная система, содержащая (4n + 2) -электронов (где n = 0,1,2…).

Правило Хюккеля

Если число электронов в аннулене можно выразить как 4n, то два из этих электронов будут располагаться на паре вырожденных МО, то молекула приобретет электронную конфигурацию бирадикала и будет отличаться повышенной химической активностью. Такие структуры называются антиароматическими.

3

n = 2 2 6 6 6

числа типа:
Рассмотрим пример трехчленного цикла. Матрица коэффициентов МО будет выглядеть

+ 2) =
= (1/6)0,5 { e i(2/3)

Таким образом, набор коэффициентов действительных МО можно записать в виде матрицы:

о

узловые плоскости

Формулы для расчета коэффициентов действительных МО в общем виде

при атоме с номером n
заселенность данной МО (число электронов)
no
число

избыточный электрический заряд, локализованный в области пространства молекулы, занимаемой данным атомом


Рассчитанные порядки относятся только к p-связям. Полные порядки связи

Индекс свободной валентности

In = Nmax - Pn

Nmax - некоторая калибровочная константа (для атомов углерода она, обычно принимается равной 1,732

Pn- сумма порядков всех связей π-типа, которые атом с номером n образует со своими соседями

диаграммы", представляющей собой топологический граф молекулы, снабженный значениями зарядов атомов,

Молекулярная диаграмма фульвена

– в виде т.н. "матрицы порядков"
квадратная матрица, размером

по диагонали ее располагаются электронные плотности атомов

недиагональным элементам соответствуют порядки -связей для данной пары атомов

Эти формулы были предложены Коулсоном, и матрица поэтому часто называется "матрицей Коулсона"

молекулы.
углеводородные молекулы
альтернантные (АУ)
неальтернантные (НАУ)
топологический граф может быть раскрашен

такую раскраску найти нельзя

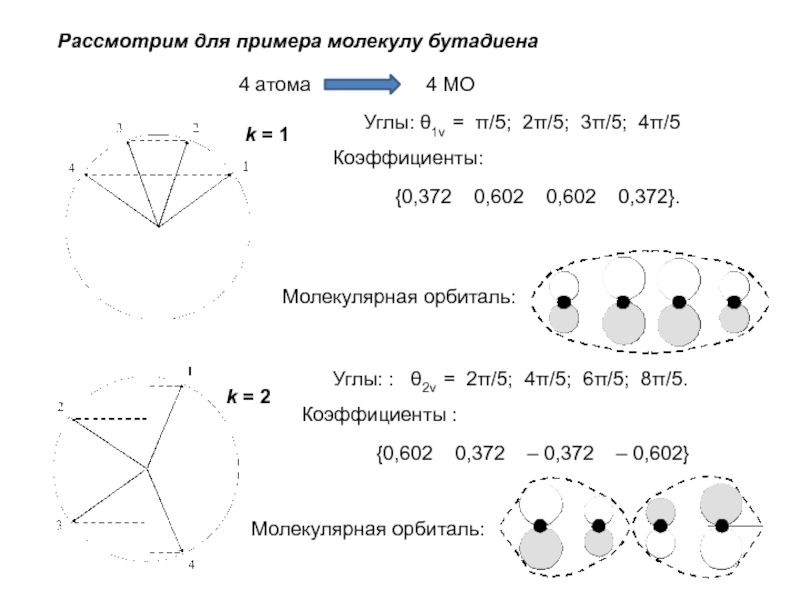
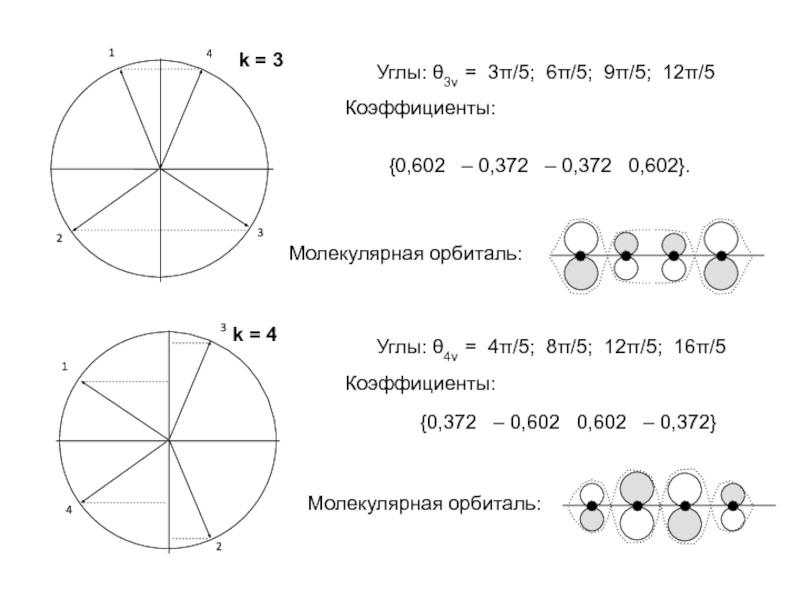
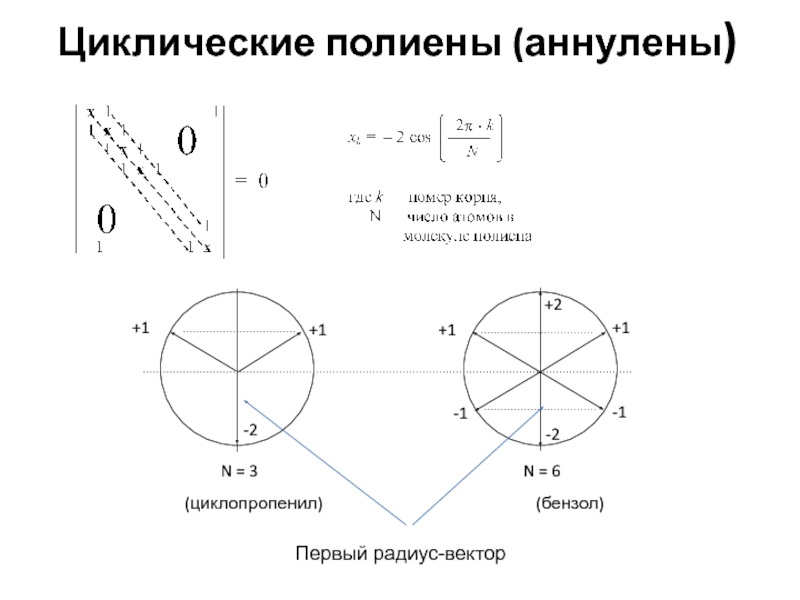
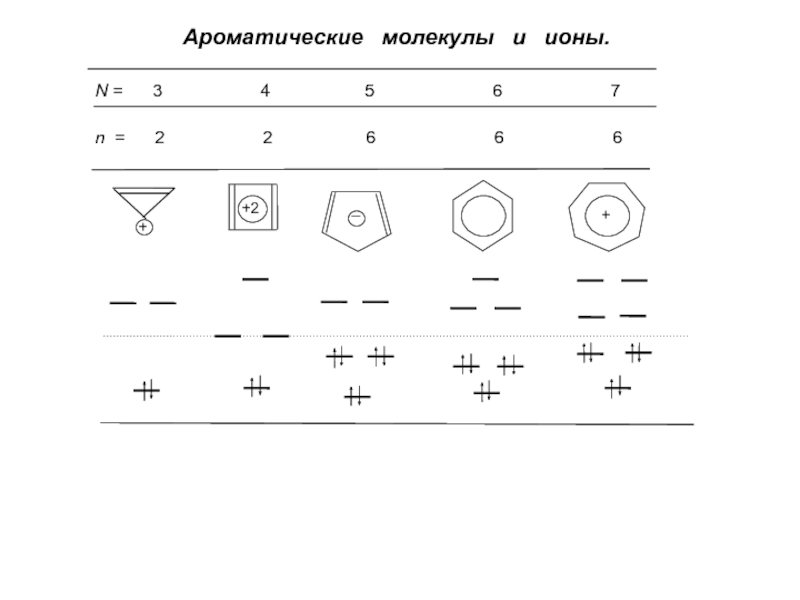
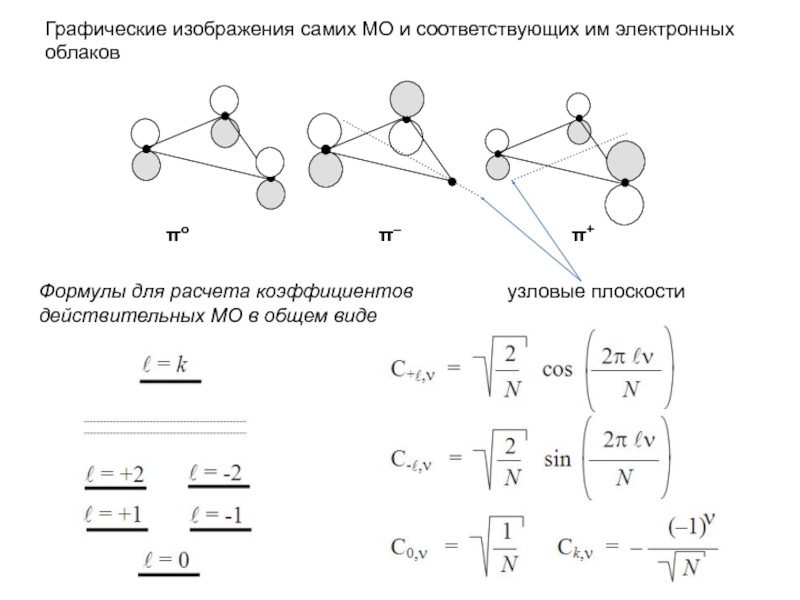
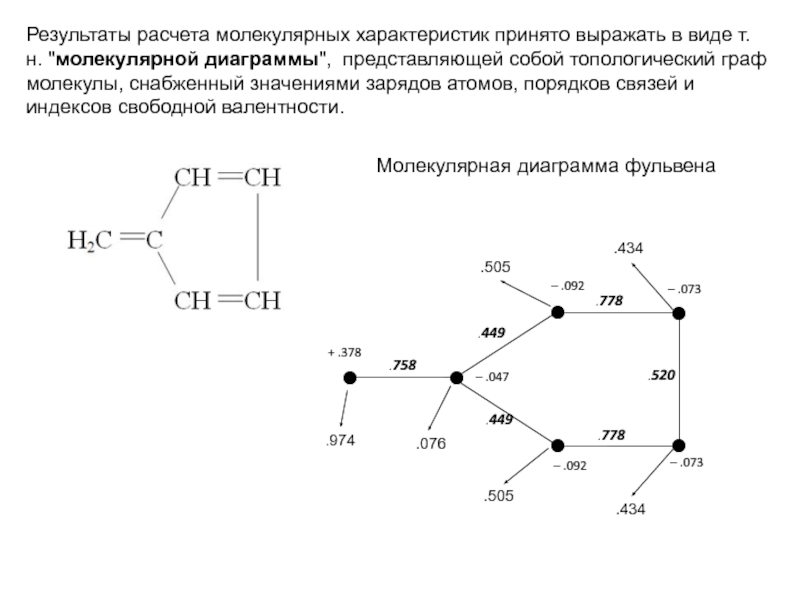
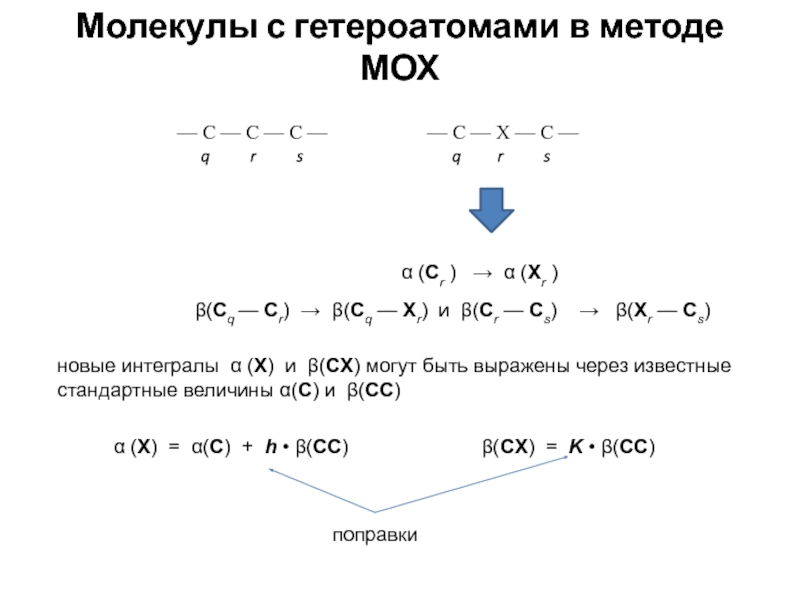
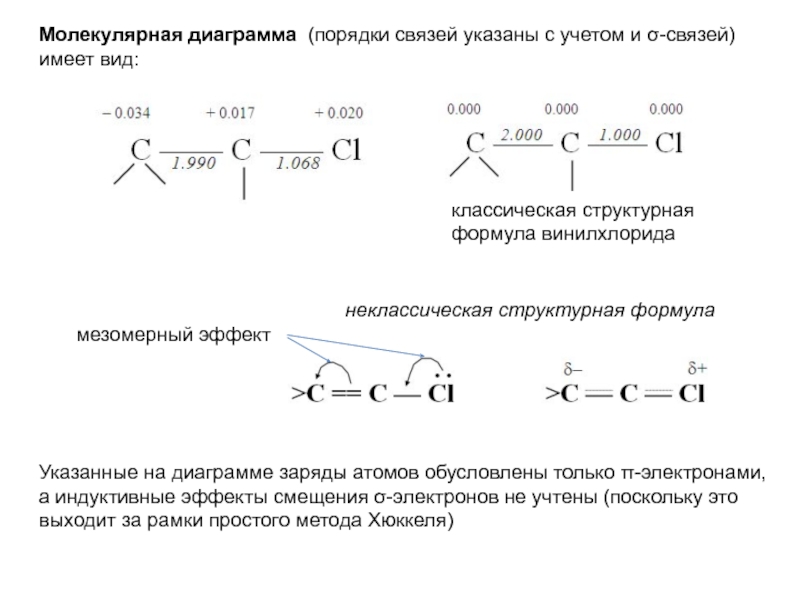
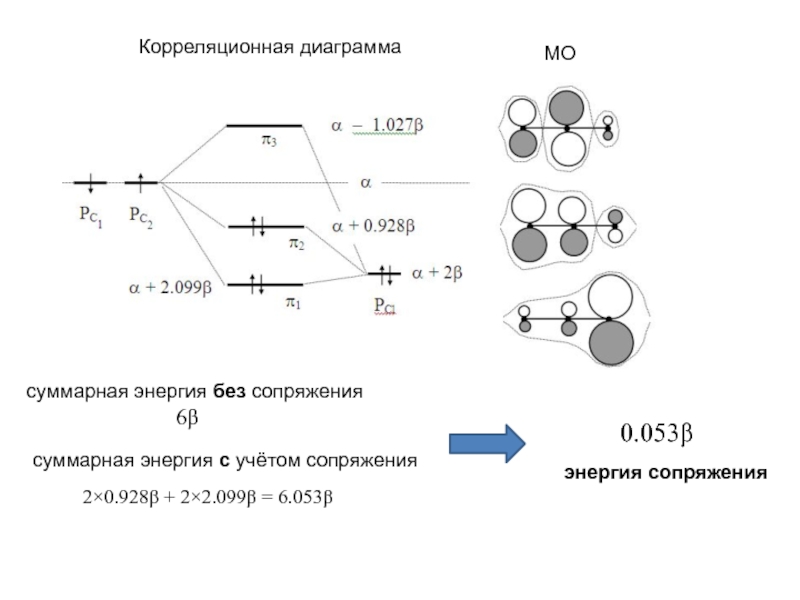
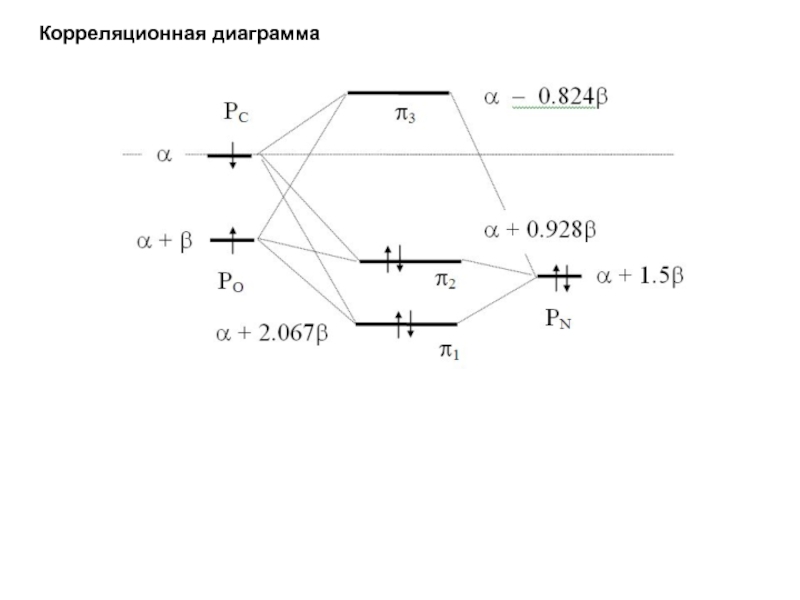
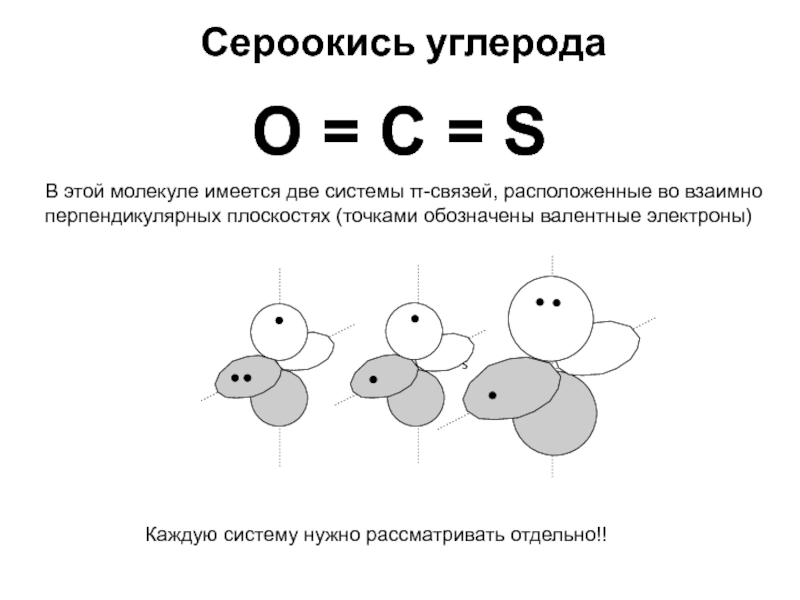
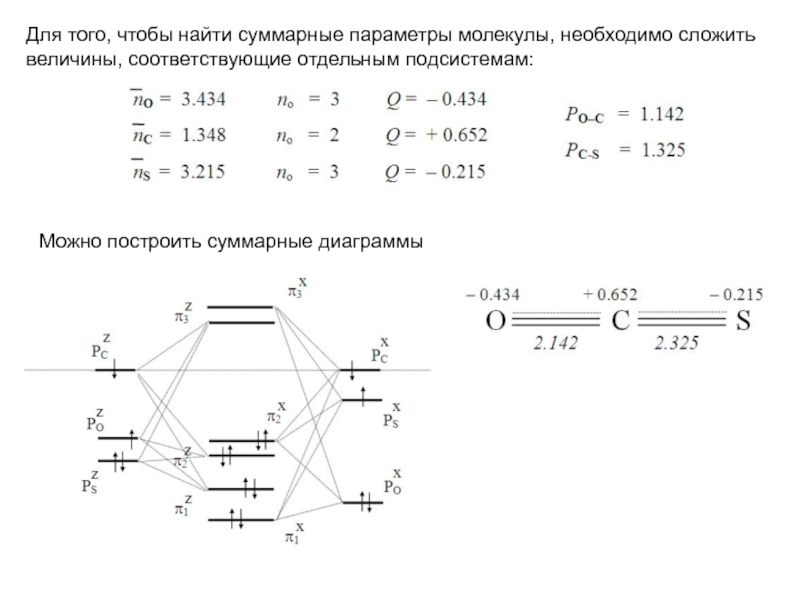
 хk
энергетические уровни расположены всегда симметрично, относительно нулевого уровня

среди них могут быть и нулевые (циклические структуры), тогда в молекуле имеется две вырожденные несвязывающие МО

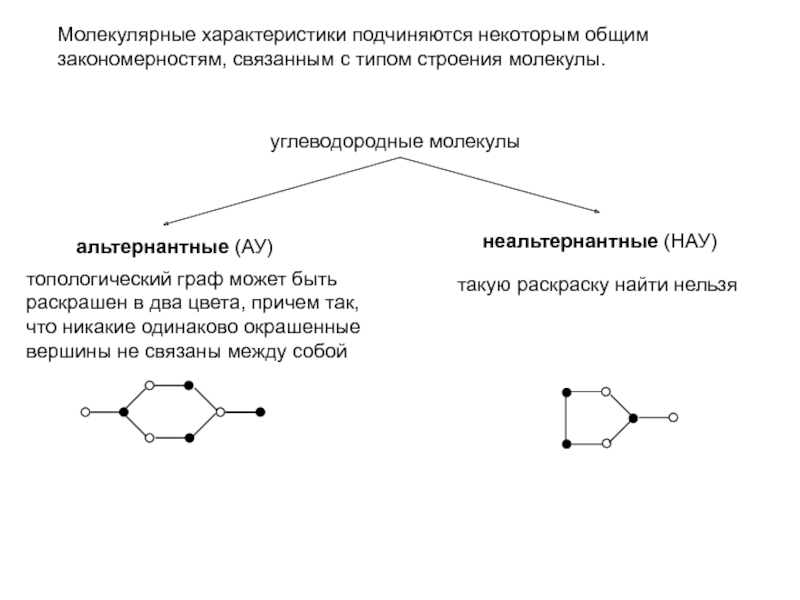
в нечетных АУ величины х имеют вид 0,  хk

среди энергетических уровней обязательно имеется и нулевой (  ), соответствующий несвязывающей МО

для нециклических НАУ все величины х различны между собой (за исключением случайных совпадений), и все энергетические уровни невырождены;

для циклических НАУ дважды вырожденные уровни располагаются несимметрично, относительно нулевого уровня и среди них нет уровня с    (несвязывающей МО)

для АУ (как четных, так и нечетных) все атомные электронные плотности равны 1, а электрические заряды атомов равны нулю (за исключением молекулярных ионов)

С —

q r s q r s

 (Сr )   (Xr )

(Cq — Cr)  (Cq — Xr) и (Cr — Cs)  (Xr — Cs)

новые интегралы  (X) и (CХ) могут быть выражены через известные стандартные величины (С) и (CС)

 (X) = (С) + h • (CС) (CХ) = K • (CС)

поправки

разница в размерах гетероатома и атома углерода
гетероатомы
>С=Х
>C=C—X:

= 2.0 K = 0.4
Решив уравнения Рутана, найдем и

Располагая коэффициентами МО и заселенностями, рассчитаем молекулярные параметры:

вид:
классическая структурная формула винилхлорида
неклассическая структурная формула
мезомерный эффект
Указанные на

суммарная энергия с учётом сопряжения
0.053b
энергия сопряжения

h = 1.5 K = 0.8
Запишем матрицу

коэффициенты МО

амидной группы:

две системы -связей, расположенные во взаимно перпендикулярных плоскостях (точками обозначены

Каждую систему нужно рассматривать отдельно!!

соответствующие отдельным подсистемам:
Можно построить суммарные диаграммы

молекул.
Во-вторых, полуэмпиричность метода приводит к необходимости экспериментального определения величины ,