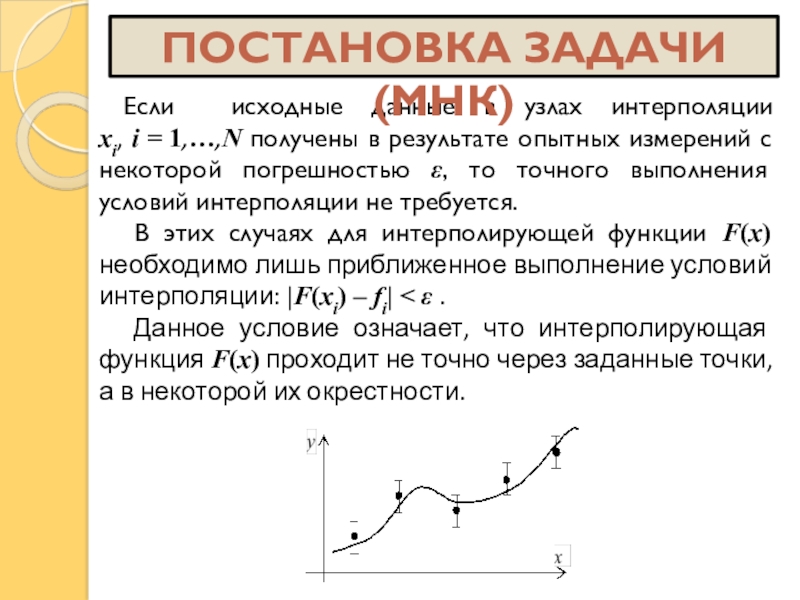
результате опытных измерений с некоторой погрешностью ε, то точного выполнения
условий интерполяции не требуется.В этих случаях для интерполирующей функции F(x) необходимо лишь приближенное выполнение условий интерполяции: |F(xi) – fi| < ε .
Данное условие означает, что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности.
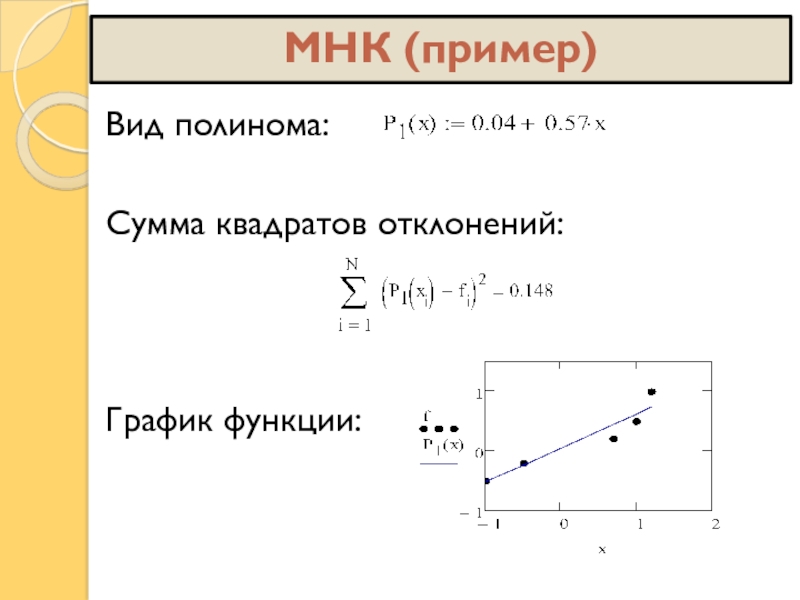
ПОСТАНОВКА ЗАДАЧИ (МНК)








![Метод наименьших квадратов (МНК) Найти значение определенного интеграладля функции f(x), заданной на некотором отрезке [a, Найти значение определенного интеграладля функции f(x), заданной на некотором отрезке [a, b].Исходя из геометрической интерпретации определенного интеграла,](/img/tmb/5/499346/b18d32cd91766d06a9beb478854eb269-800x.jpg)


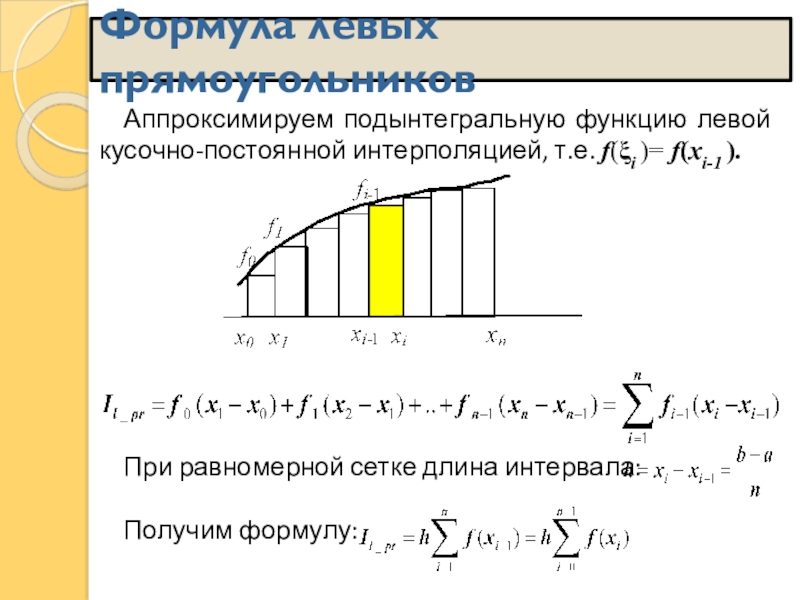

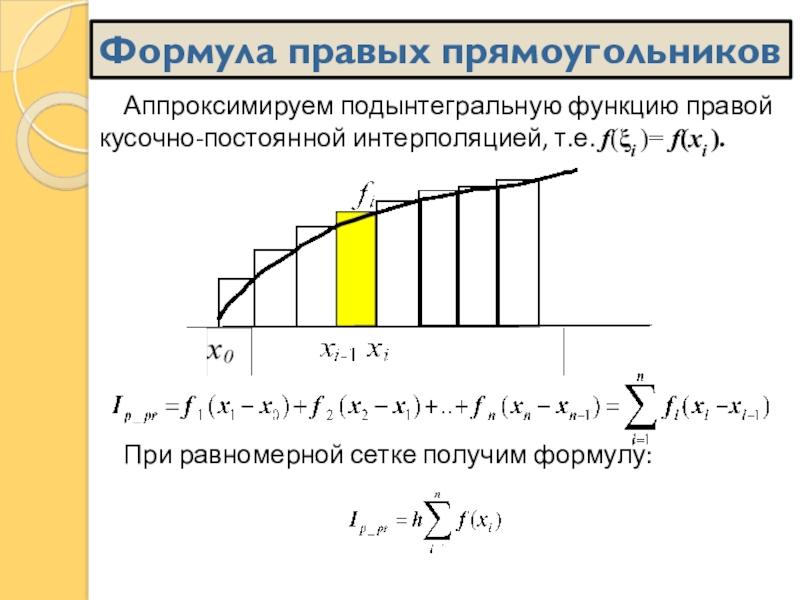
![Метод наименьших квадратов (МНК) Заменим на каждом локальном отрезке [xi-1, xi] значение подынтегральной функции на Заменим на каждом локальном отрезке [xi-1, xi] значение подынтегральной функции на ее значение в середине интервала, т.е.](/img/thumbs/e9f10b4752767824f7538a627a8fa888-800x.jpg)
![Метод наименьших квадратов (МНК) На каждом локальном отрезке [xi-1, xi] аппроксимируем подынтегральную функцию линейной зависимостью На каждом локальном отрезке [xi-1, xi] аппроксимируем подынтегральную функцию линейной зависимостью (кусочно-линейная интерполяция). В этом случае криволинейная](/img/thumbs/02d140e4c870c77b172039b40410a947-800x.jpg)
![Метод наименьших квадратов (МНК) На каждом локальном отрезке [xi-1, xi] аппроксимируем подынтегральную функцию кусочно-параболической зависимостью, На каждом локальном отрезке [xi-1, xi] аппроксимируем подынтегральную функцию кусочно-параболической зависимостью, т.е. параболой, проходящей через три точки:](/img/thumbs/17957688e202e9c13e89cbd5941dd6cc-800x.jpg)