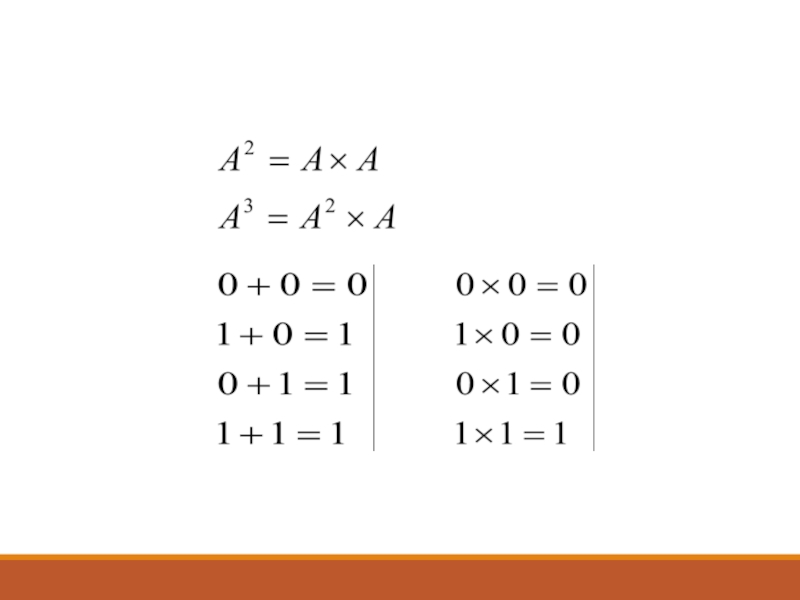Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы и приемы реализации математических моделей теплотехнических систем
Содержание
- 1. Методы и приемы реализации математических моделей теплотехнических систем
- 2. Расчет тепловой технологической схемы заключается в нахождении
- 3. Первый метод заключается в решении СБУ одним
- 4. Модульный метод. Для разомкнутых систем данный метод
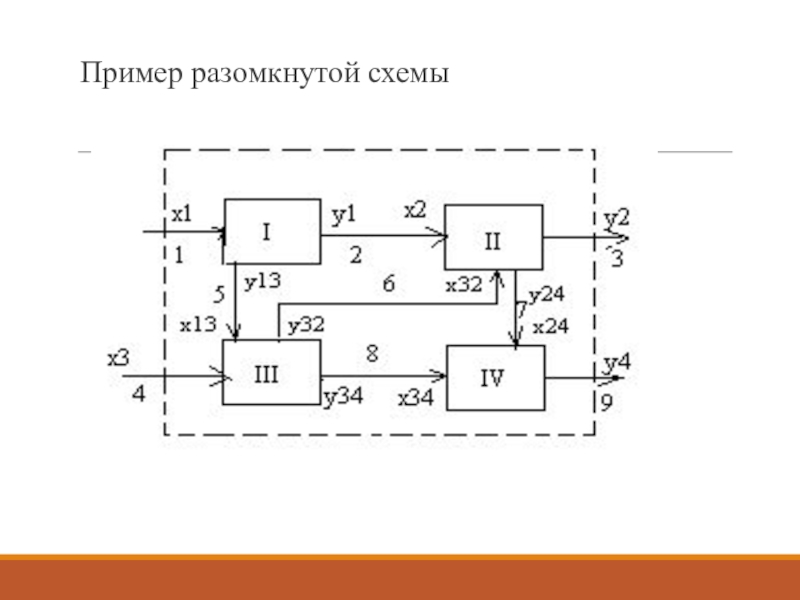
- 5. Пример разомкнутой схемы
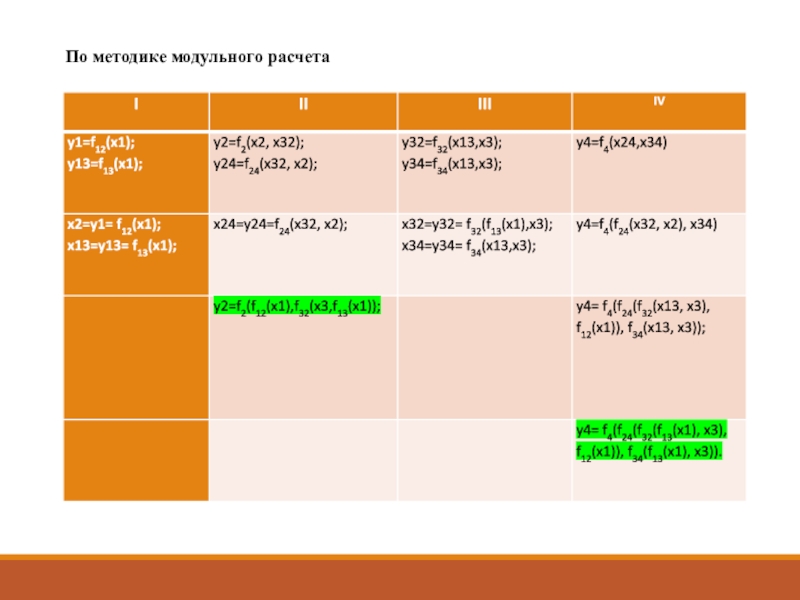
- 6. По методике модульного расчета
- 7. Для небольших схем порядок расчета может быть
- 8. Матрица процессов на примере схемы для ГТУ
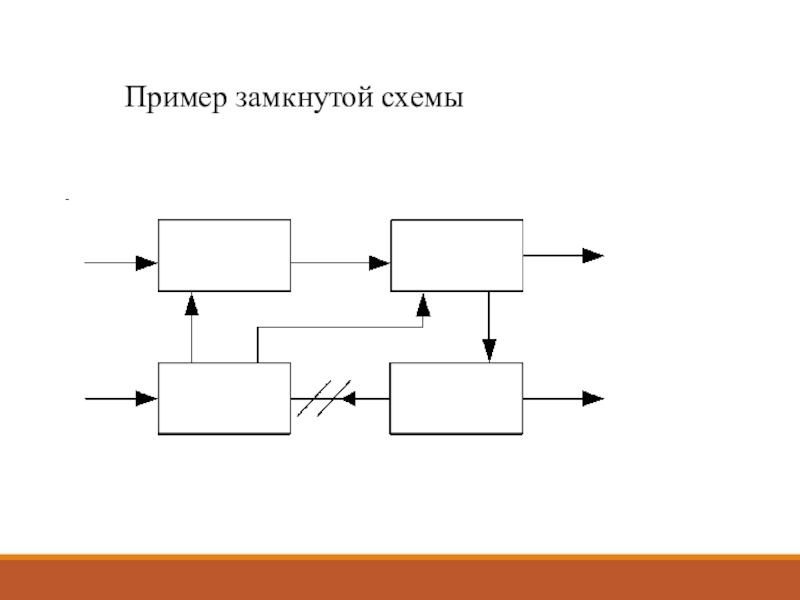
- 9. Пример замкнутой схемы
- 10. Исходными (известными) являются связи 1 и 4.
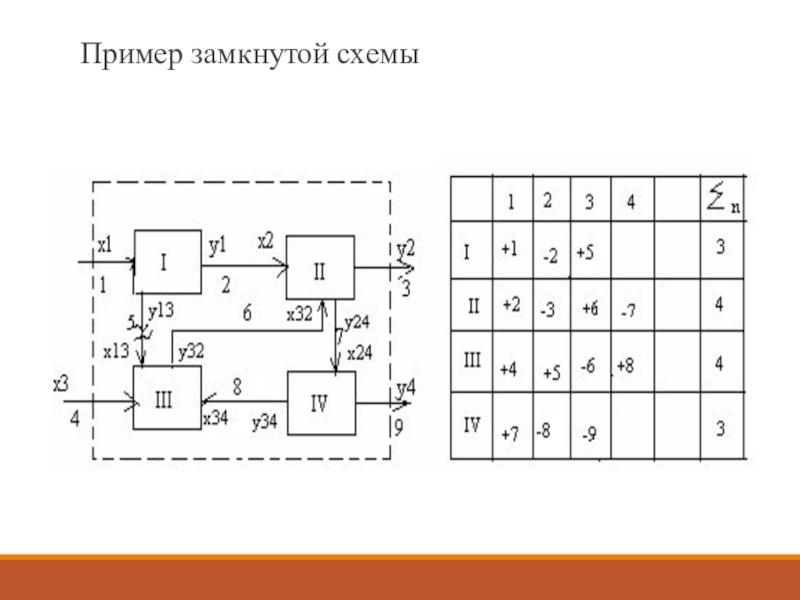
- 11. Пример замкнутой схемы
- 12. Таким образом, последовательность расчета замкнутой схемы можно
- 13. Матрица смежности
- 14. Единица в ij эл-те матрицы смежности является
- 15. В результате этого перемножения в главной диагонали
- 16. Слайд 16
- 17. 1-ца в ij эл-те матрицы контуров является
- 18. Слайд 18
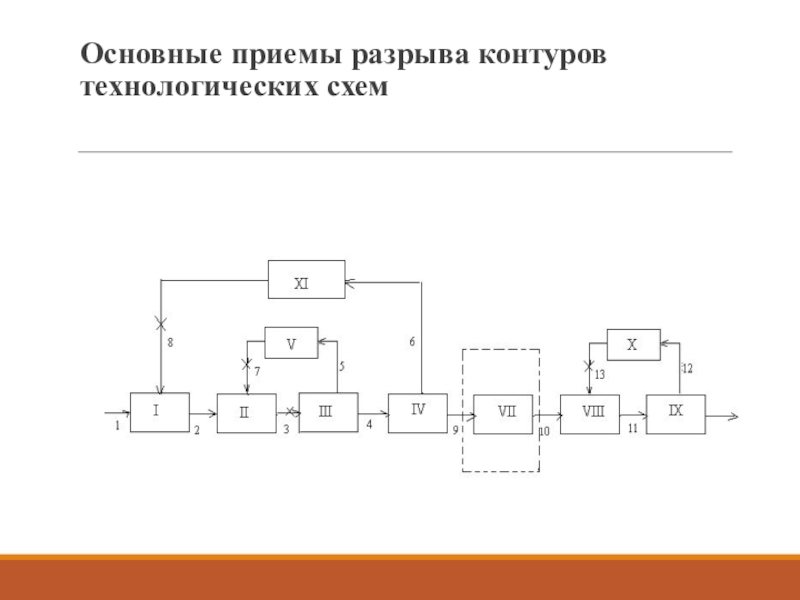
- 19. Основные приемы разрыва контуров технологических схем
- 20. Данная схема состоит из 10 эл-ов и
- 21. Слайд 21
- 22. Однако если учесть, что 3 контур независим
- 23. Очевидно, если разорвать связи 7, 8, 13,
- 24. При этом правильный выбор разрываемых потоков или
- 25. СПАСИБО ЗА ВНИМАНИЕ!Минск 29 апреля 2020 года
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Скачать презентанцию
Расчет тепловой технологической схемы заключается в нахождении точных значений параметров всех потоков, а при необходимости и конструктивных пар-ров, которые удовлетворяют как уравнения системы балансовых уравнений, так и моделям всех элементов, а
Слайды и текст этой презентации
Слайд 1Методы и приемы реализации математических моделей теплотехнических систем макроуровня
(продолжение)
ИЮНЬ 2020
г.
Слайд 2Расчет тепловой технологической схемы заключается в нахождении точных значений параметров
всех потоков, а при необходимости и конструктивных пар-ров, которые удовлетворяют
как уравнения системы балансовых уравнений, так и моделям всех элементов, а так же системе ограничений на параметры.Различают 3 подхода к расчету технологической схемы:
интегральный метод (одновременный расчет всех неизвестных);
последовательный (модульный) расчет;
комбинированный (модульно-интегральный) расчет.
Методики расчета ТТС
(систем балансовых уравнений)
Слайд 3Первый метод заключается в решении СБУ одним из итерационных методов,
обычно применяется в том случае, если модели всех элементов либо
линейные, либо могут быть приведены к квазилинейному виду.Второй метод основан на использовании анализа структуры теплотехнической системы и представление модели ее элементов в виде зависимости между входными и выходными параметрами. Он заключается в последовательном, элемент за элементом расчете.
Заключается в том, что расчет СБУ выполняется с учетом структуры теплотехнической системы. В данном случае определяется оптимальная последовательность решений уравнений исходя из анализа структуры схемы.
Слайд 4
Модульный метод. Для разомкнутых систем данный метод предпочтителен и, как
правило, не вызывает трудностей для определения последовательности элементов.
Для большинства ТТС
характерны схемы с множеством обратных связей, т.е. существование контуров. В этом случае для применения последовательного метода расчета необходимо выявить разомкнутую схему эквивалентную исходной замкнутой. Другими словами определить связи, по которым происходит разрыв контуров, после чего происходит итерациональный расчет методом последовательных приближений.Слайд 7Для небольших схем порядок расчета может быть определен простым перебором
вариантов расчета, для более сложных используется матрица процессов.
Прямоугольная матрица, в
которой строки соответствуют номерам элементов, а столбцы порядковому номеру связи. Таким образом, ij элемент матрицы процессов равен номеру связи со знаком плюс для входящей в i элемент и со знаком минус для выходящей из него связи.Поэтому если последовательно просматривать строки матрицы и находить элементы с известными параметрами входящих связей означает, что этот элемент может быть рассчитан по его модели, и следовательно, параметры выходящих из него связей пополняют число известных параметров. Таким образом, в последовательном итерационном процессе можно определить последовательность расчета схемы, а, следовательно, и теплотехнической системы.
Слайд 10Исходными (известными) являются связи 1 и 4. Легко видеть, в
том числе и из матрицы процессов, что последовательный расчет схемы
не возможен. Одним из приемов расчета замкнутых схем, т.е. имеющих контура, является переход к эквивалентно-разомкнутой схеме. Путем разрыва связи 5 и задания параметров этой связи, наша схема превращается в разомкнутую эквивалентной исходную замкнутой схеме. При этом эквивалентность будет соблюдаться только в том случае, если будет соблюдаться равенство параметров в точке разрыва.Очевидно, если использовать методику построения комбинированных математических моделей, рассмотренную ранее, в этом случае мы можем вывести обобщенную математическую модель итерационного вида.
Слайд 12Таким образом, последовательность расчета замкнутой схемы можно представить в следующем
виде:
1) определяются все контура схемы;
2) определяются оптимальные точки разрыва для
перехода к эквивалентно-разомкнутой схеме;3) в точках разрыва связи задаются параметры связей;
4) производится итерационный расчет схемы по условию схождения параметров в точках разрыва с заданной точностью.
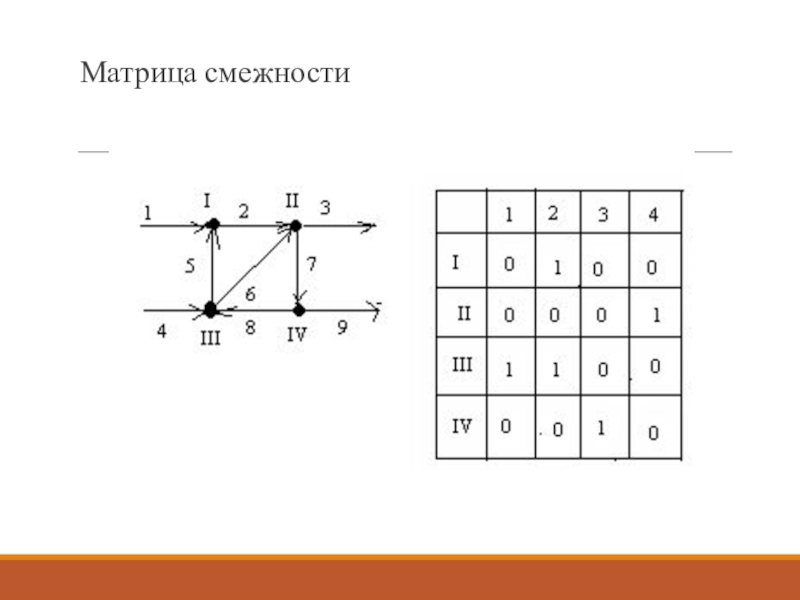
Для формализации определения контуров в схеме используется матрица смежности, которая представляет собой квадратную матрицу, строки и столбцы которой обозначают номера элементов схемы.
Слайд 14Единица в ij эл-те матрицы смежности является принципом существования связи,
выходящей из i-го эл-та и входящей в j-ый элемент.
После
составления матрицы смежности производится ее анализ на наличие пустых столбцов и пустых строк. Если таковые существуют, то они исключаются из матрицы и получают сокращенную матрицу смежности. Пустая строка означает, что из данного элемента не выходит ни одной внутренней связи. Пустой столбец означает, что в данный элемент не входит ни одна внутренняя связь. Далее производится умножение сокращенной матрицы смежности саму на себя, по правилам булевой алгебры.
Слайд 15В результате этого перемножения в главной диагонали матрицы будет появляться
единицы, что будет означать, что данный элемент косвенно оказывает влияние
сам на себя, а, следовательно, входит в контур.Для определения оптимальной точки разрывов, а, следовательно, оптимальной последовательности расчета схемы, используется матрица контуров, которых представляет собой прямоугольную матрицу, строки обозначает порядковый номер контура, а столбцы номера внутреннюю связь.
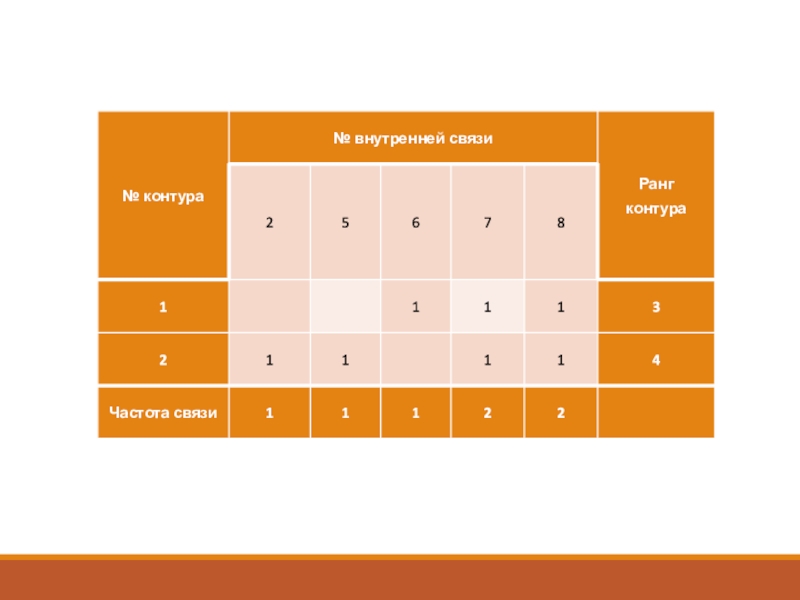
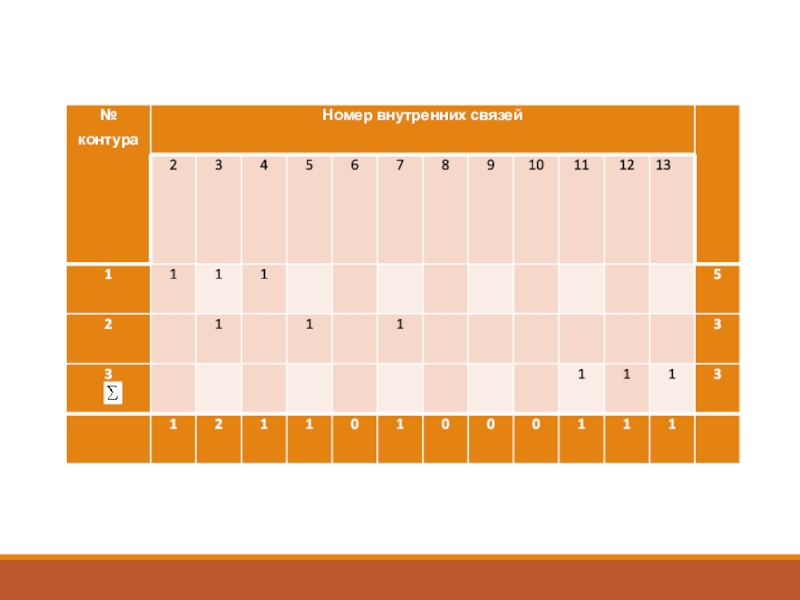
Слайд 171-ца в ij эл-те матрицы контуров является признаком, что j-ая
связь входит в i-ый контур. Оптимальной точкой разрыва является связь
с максимальной частотой, входящая в контур с максимальным рангом.Если имеется выбор по связям, как между 7 и 8 (в данном случае), то выбирается связь с наименьшим числом параметров.
Слайд 20Данная схема состоит из 10 эл-ов и 14 связей, и
содержит 3 контура:
I-II-III-IV-VI-I,
II-III-V-II,
VIII-IX-X-VIII.
Первые 2 контура взаимосвязаны и являются контурами 1
ранга. Третий контур независимый от первых двух и является контуром нулевого ранга.
Слайд 22Однако если учесть, что 3 контур независим от первых двух,
что отражается на схеме тем, что данную систему уравнений можно
разделить на 2 подсистемы, по связи 9-10, слабым связям, т.е. вводная система разбивается на 2 подсистемы состоящие, соответственно из 6 и из 3 уравнений.Дальнейший анализ показывает, так как 1 и 2 контуры взаимосвязаны, то они имеют общие связи, разрыв одной из которых приводит к разрыву сразу обоих контуров. В данной схеме такой связью является связь 3: следовательно, окончательно, мы имеем 2 замыкающие системы уравне-ний по связям 3 и 13, каждая из которых состоит из 3 уравнений. Следовательно, в сложных технологических имеются оптимальные варианты перехода от замкнутой структуры, к условно разомкнутой.
Слайд 23Очевидно, если разорвать связи 7, 8, 13, мы будем иметь
замыкающую систему уравнений, состоящую из 9 уравнений, если все связи
будут 3-х параметрическими.Слайд 24При этом правильный выбор разрываемых потоков или связей, позволяет существенно
понизить размерность системы замыкающих нелинейных уравнений к решению которых сводится
расчет технологической схемы, или заменить систему уравнений высокого порядка на несколько независимых систем более низкого порядка. Применяют две основные операции с помощью которых возможно понизить размерность решаемой задачи:1-ая операция заключается в том, что в схеме необходимо выделять элементы охваченные контурами и элементы, не входящие ни в один из контуров. Тогда схему можно разделить на подсистемы. И расчет всей схемы можно разделить на расчет систем уравнений для отдельных контуров и расчет элементов, не входящих в контуры.
2-ая операция – выбор внутри каждого контура, в определенном смысле наилучших совокупностей связей, разрыв которых превращает в контур разомкнутую схему. Наилучшей можно назвать такую совокупность связей, сумма параметров которой является минимальной.