Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы зондирования окружающей среды
Содержание
- 1. Методы зондирования окружающей среды
- 2. Эффективная площадь рассеяния (ЭПР) электромагнитных волнрадиолокационной целью
- 3. При радиолокационных наблюдениях рассеивающие свойства целей
- 4. При этом, если излучение и прием осуществляется
- 5. Рассмотрим вывод выражения для эффективной площадью
- 6. Эффективная площадь рассеяния объекта σ в
- 7. RP1P2 При равномерном рассеивании во все стороны энергии
- 8. ЭПР зависит от электрических свойств
- 9. Достаточно просто теоретически ЭПР может быть
- 10. Коэффициенты an и bn
- 11. Запишем выражение для при следующих упрощающих
- 12. Для таких малых частиц сферической формы описывается формулой Релея:
- 13. Множитель для воды в сантиметровом диапазоне
- 14. С увеличением размеров частиц, когда a
- 15. Пространственно-распределенные метеорологические цели Эффективная площадь рассеяния единицы объема
- 16. Пространственно-распределенные метеорологические цели формируют отраженные сигналы, создаваемые
- 17. Если положение рассеивающих частиц в объеме взаимно
- 18. Теоретически наиболее просто можно рассчитать удельную ЭПР
- 19. С учетом закона распределения рассеивающих частиц по
- 20. Разрешаемый объем метеорологической цели
- 21. Эффективная площадь рассеяния реальной метеорологической цели
- 22. При использовании импульсных РЛС разрешаемый объем метеорологической
- 23. При длительности формируемого РЛС импульса, равного ,
- 24. Однако сигналы, отраженные от частиц, заполняющих данный
- 25. В результате для узкой симметричной диаграммы направленности
- 26. Тогда, в случае релеевского рассеяния для монодисперсных метеорологических объектов их ЭПР будет описываться следующим выражением:
- 27. Напомним, что ширина угла диаграммы направленности параболических
- 28. Полученные выше выражения для ЭПР справедливы в
- 29. Радиолокационная отражаемость
- 30. Удельная ЭПР метеорологического объекта η при
- 31. Величина называется радиолокационной отражаемостью. Радиолокационная отражаемость Za
- 32. Величина радиолокационной отражаемости Zа в отличие
- 33. Радиолокационная отражаемость Za определяется концентрацией и распределением
- 34. Формулы для Za и выражают еще
- 35. Радиолокационная отражаемость является одной изб основных характеристик,
- 36. Радиолокационная отражаемость Za является специфической метеорологической характеристикой
- 37. Величина радиолокационной отражаемости Za измеряется в м6/м3
- 38. В связи с тем, что
- 39. Отражаемость облаков
- 40. Расчет интенсивности рассеяния электромагнитной энергии
- 41. Функция распределения облачных капель по размерам f(a)
- 42. Спектр капель для облаков можно аппроксимировать формулой
- 43. Для вычисления радиолокационной отражаемости можно использовать такую
- 44. Отражаемость жидких осадков
- 45. Капли мороси и дождя значительно крупнее облачных.
- 46. Функция распределения капель даже для одного облака
- 47. При использовании функции распределения частиц осадков по
- 48. Соотношение, ,которое иногда называют Z I
- 49. Отражаемость снегопада
- 50. Для снегопада установлено, что в среднем Z
- 51. Какие будут вопросы ?
- 52. Среднее распределение капель дождя по
- 53. Слайд 53
- 54. При использовании импульсных РЛС разрешаемый объем метеорологической
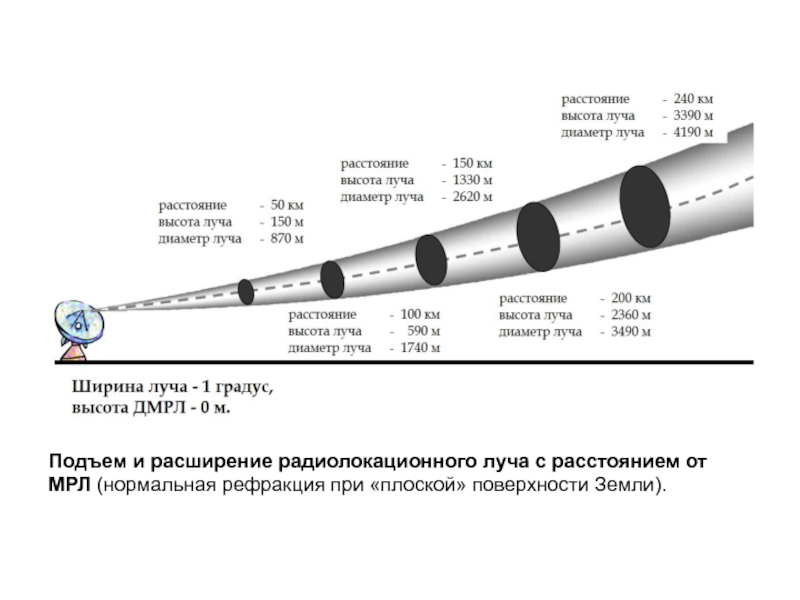
- 55. Подъем и расширение радиолокационного луча с расстоянием от МРЛ (нормальная рефракция при «плоской» поверхности Земли).
- 56. Диаграмма направленности антенны
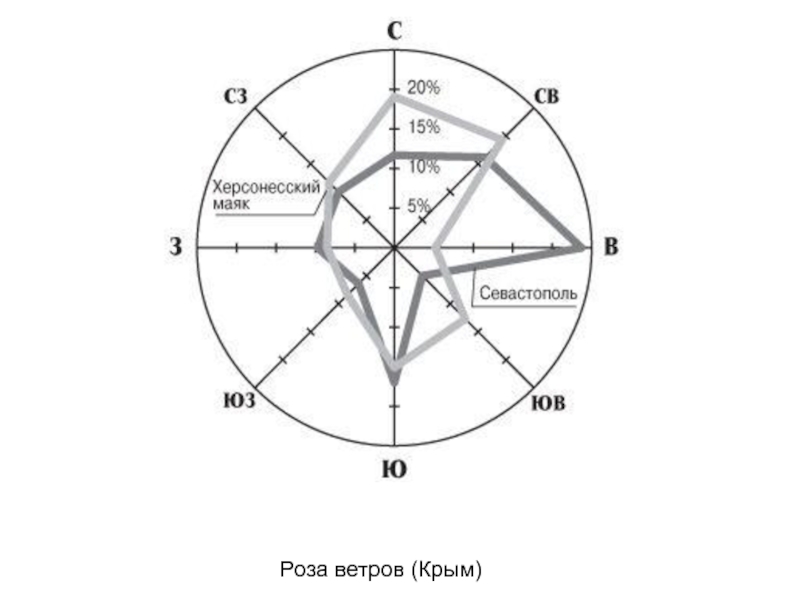
- 57. Роза ветров (Крым)
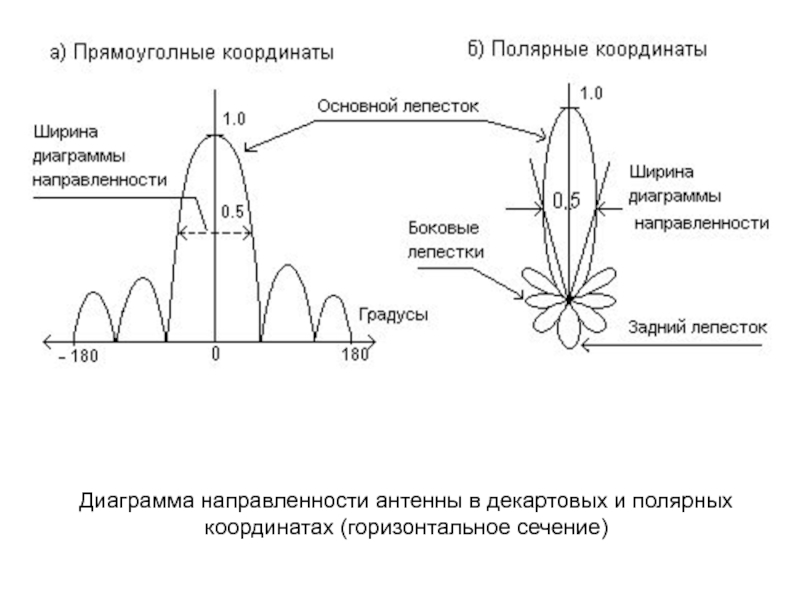
- 58. Диаграмма направленности антенны в полярных координатах (горизонтальное сечение)
- 59. Слайд 59
- 60. Диаграмма направленности антенны в декартовых и полярных координатах (горизонтальное сечение)
- 61. Скачать презентанцию
Эффективная площадь рассеяния (ЭПР) электромагнитных волнрадиолокационной целью
Слайды и текст этой презентации
Слайд 1Методы зондирования окружающей среды
Профессор Кузнецов Анатолий Дмитриевич
Рассеяние электромагнитных волн атмосферными
образованиями
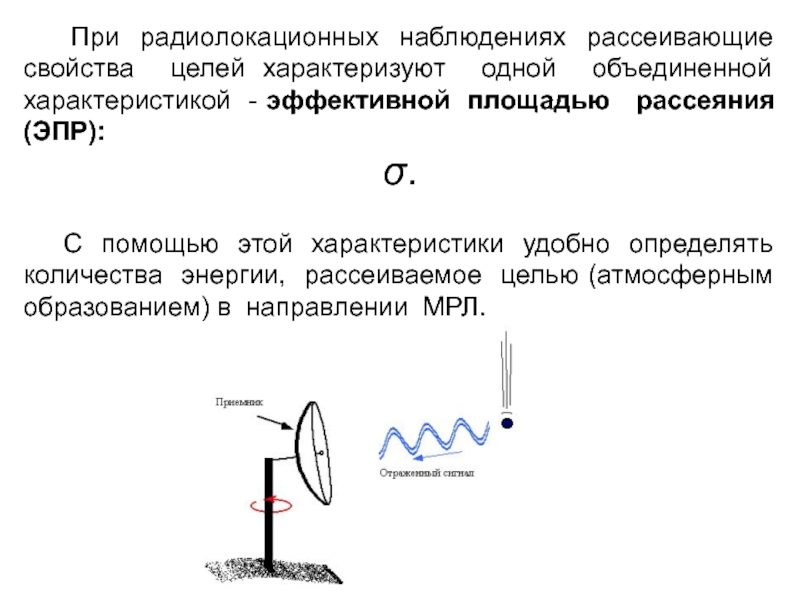
Слайд 3 При радиолокационных наблюдениях рассеивающие свойства целей характеризуют одной объединенной
характеристикой - эффективной площадью рассеяния (ЭПР):
σ.
С помощью
этой характеристики удобно определять количества энергии, рассеиваемое целью (атмосферным образованием) в направлении МРЛ. Слайд 4 При этом, если излучение и прием осуществляется в одной точке
пространства (на одну антенну), то для описания рассеивающих свойств радиолокационной
цели используется термин эффективная площадь обратного рассеяния.Слайд 5
Рассмотрим вывод выражения для эффективной площадью рассеяния σ
при следующих предположениях:
- рассеивающая поверхность цели расположена перпендикулярно падающему
лучу;- падающая на цель энергия P1 рассеивается равномерно во всех направлениях.
Слайд 6 Эффективная площадь рассеяния объекта σ в предположении, что падающая
на него энергия рассеивается равномерно во всех направлениях, равна
где
P1 - плотность потока мощности электромагнитной волны, пришедшего от МРЛ, в точке расположения объекта,
P2 - плотность потока мощности электромагнитной волны, рассеянной объектом и оказавшейся в точке расположения МРЛ;
R - расстояние от МРЛ до объекта.
Слайд 7R
P1
P2
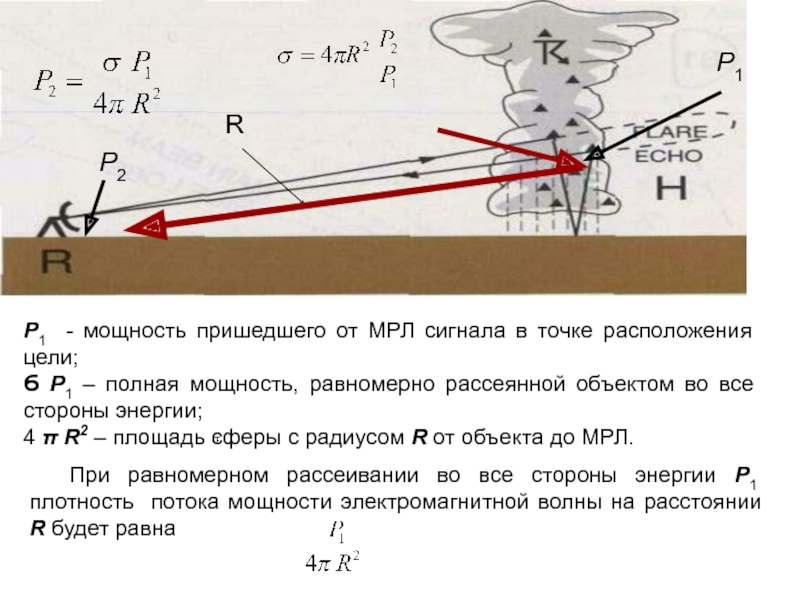
При равномерном рассеивании во все стороны энергии P1 плотность потока
мощности электромагнитной волны на расстоянии R будет равна
P1 -
мощность пришедшего от МРЛ сигнала в точке расположения цели;Ϭ P1 – полная мощность, равномерно рассеянной объектом во все стороны энергии;
4 π R2 – площадь сферы с радиусом R от объекта до МРЛ.
Слайд 8 ЭПР зависит от электрических свойств материала объекта, его
конфигурации, геометрических размеров и направления, с которого происходит облучение.
Применительно
к атмосферным образованиям сделанное определение ЭПР относится лишь к единичной локационной цели, в качестве которой, например, можно рассматривать отдельную облачную частицу.Для большинства объектов ЭПР можно определить лишь экспериментально; теоретически величина ЭПР может быть рассчитана только для объектов с заданными свойствами и простейших геометрических форм.
Слайд 9 Достаточно просто теоретически ЭПР может быть вычислена для частиц
несложной формы, в частности, сферических. Согласно теории Густава Ми (1908
г.), ЭПР сферической частицы выражается формулойгде an и bn комплексные коэффициенты.
Слайд 10
Коэффициенты an и bn могут быть сравнительно
легко вычислены лишь при упрощающих условиях, когда для расчета ЭПР
можно применять теорию Релея, описывающую рассеяние электромагнитного излучения на частицах, размеры которых a существенно меньше длины волны λ:a << λ.
Слайд 11 Запишем выражение для при следующих упрощающих условиях:
- радиус частицы
a намного меньше длины волны : a 0.03
;- для радиуса частицы a дополнительно выполняется следующее условие:
a < 0.13 / I m I,
где m – комплексный коэффициент преломления материала частицы.
Слайд 13 Множитель
для воды в сантиметровом диапазоне длин волн равен
0.930.04, а а для льда с единичной плотностью: 0.197.
Отсюда следует, что величина эффективной площадью рассеяния для водяной сферической частицы почти в пять раз больше, чем для ледяной сферической частицы тех же размеров.
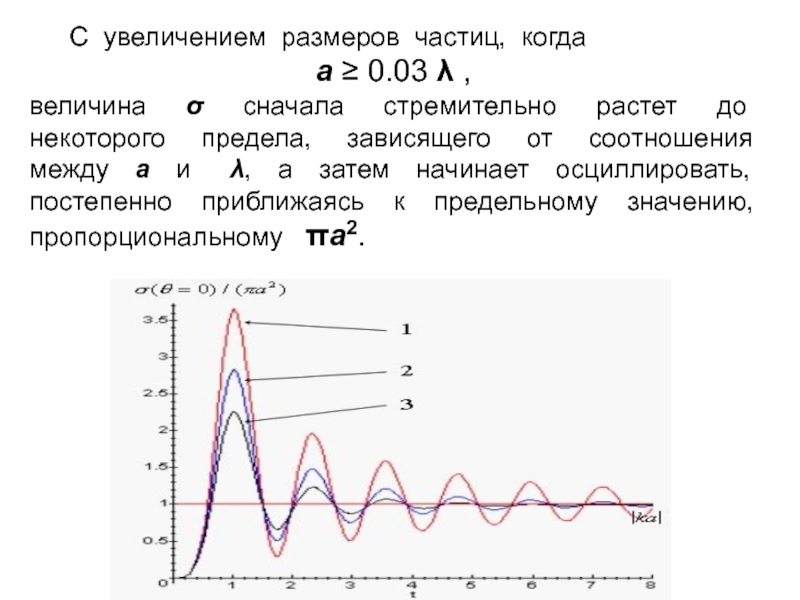
Слайд 14 С увеличением размеров частиц, когда
a 0.03
,
величина сначала стремительно растет до некоторого предела, зависящего
от соотношения между a и , а затем начинает осциллировать, постепенно приближаясь к предельному значению, пропорциональному a2. Слайд 15Пространственно-распределенные
метеорологические цели
Эффективная площадь рассеяния единицы объема
Слайд 16 Пространственно-распределенные метеорологические цели формируют отраженные сигналы, создаваемые не одной частицей,
а совокупностью частиц, которые заключены в разрешаемом объеме.
Поэтому для
характеристики эффективной площади рассеяния совокупности частиц пользуются понятием об эффективной площади рассеяния единицы объема : Слайд 17 Если положение рассеивающих частиц в объеме взаимно независимо и произвольно,
а расстояние между частицами такое, что отсутствует взаимодействие (интерференция)
между полями, создаваемыми при рассеянии отдельными частицами, то такое рассеяние является некогерентным (не согласованным). В этом случает.е. эффективная площадь рассеяния единицы объема равна сумме эффективных площадей рассеяния i отдельных частиц, находящихся в единице рассеивающего объема.
Величину часто называют удельной ЭПР.
Слайд 18 Теоретически наиболее просто можно рассчитать удельную ЭПР монодисперсных атмосферных образований,
состоящих из одинаковых по размеру и составу частиц сферической формы.
Предполагая, что суммарная мощность отраженных сигналов определяется суммой ЭПР отдельных рассеивателей, можно записать
= N i ,
где N количество рассеивающих частиц в единице объема.
Слайд 19
С учетом закона распределения рассеивающих частиц по размерам: N(a), выражение
для удельной ЭПР, содержащей информацию о метеорологических объектах в атмосфере
(облаках, осадках и т.п.); будет иметь видгде - эффективная площадь рассеяния частицы, имеющей радиус a, на длине волны λ, N(a) – функция распределения капель по размерам.
Удельная эффективная площадь рассеяния единицы объема имеет размерность м2/м3 = м-1.
Слайд 21
Эффективная площадь рассеяния реальной метеорологической цели может существенно
отличаться от величины удельной ЭПР.
Это происходи из-за того, что
при использовании радиометеорологического метода зондирования рассеянный сигнал формируется:- не точечной целью (например, самолетом);
- не единицей объема (как для удельной ЭПР).
При радиометеорологическом зондировании рассеянный сигнал формируется в пределах так называемого разрешаемого объема метеорологической цели.
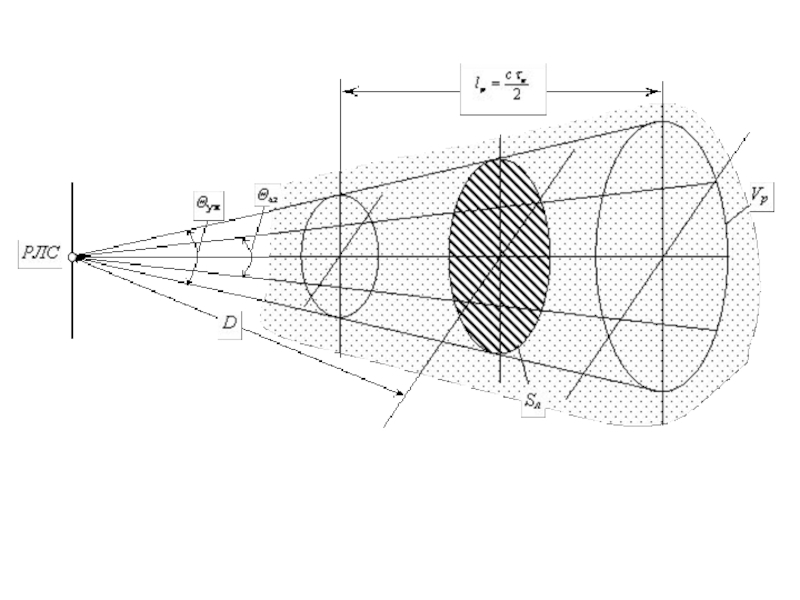
Слайд 22
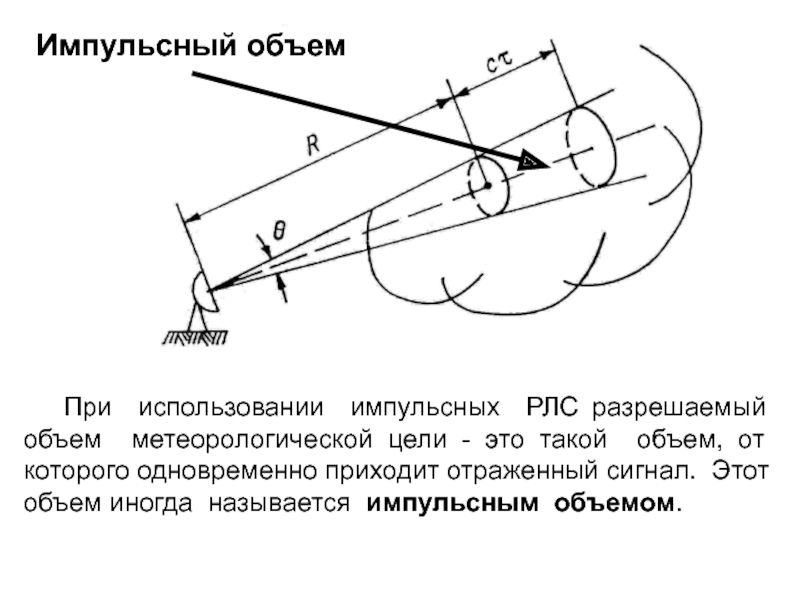
При использовании импульсных РЛС разрешаемый объем метеорологической цели - это
такой объем, от которого одновременно приходит отраженный сигнал. Этот объем
иногда называется импульсным объемом.Импульсный объем
Слайд 23
При длительности формируемого РЛС импульса, равного , занимаемый этим импульсом
в пространстве объем в любой момент времени будет равен объему
цилиндра с площадью основания S (зависящего от дальности R) и высотой L = с (с – скорость света):V = S L.
Слайд 24
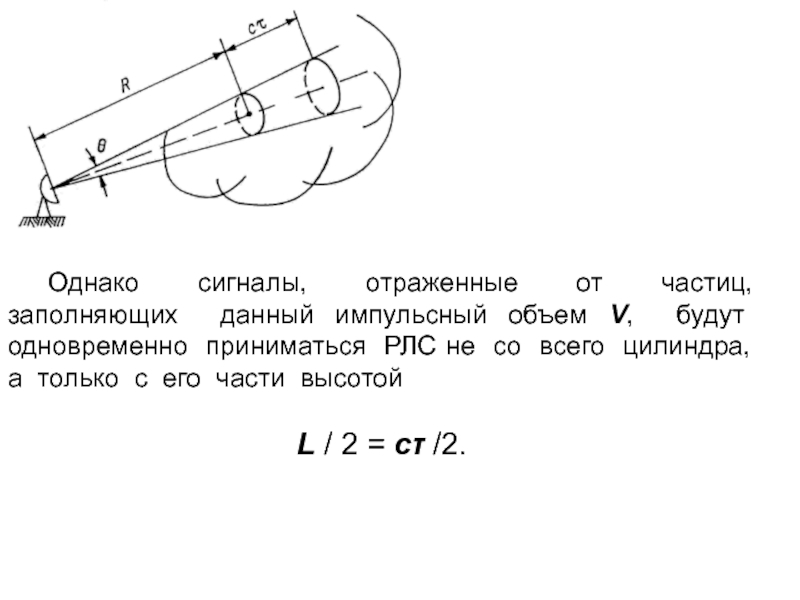
Однако сигналы, отраженные от частиц, заполняющих данный импульсный объем V,
будут одновременно приниматься РЛС не со всего цилиндра, а только
с его части высотойL / 2 = с /2.
Слайд 25
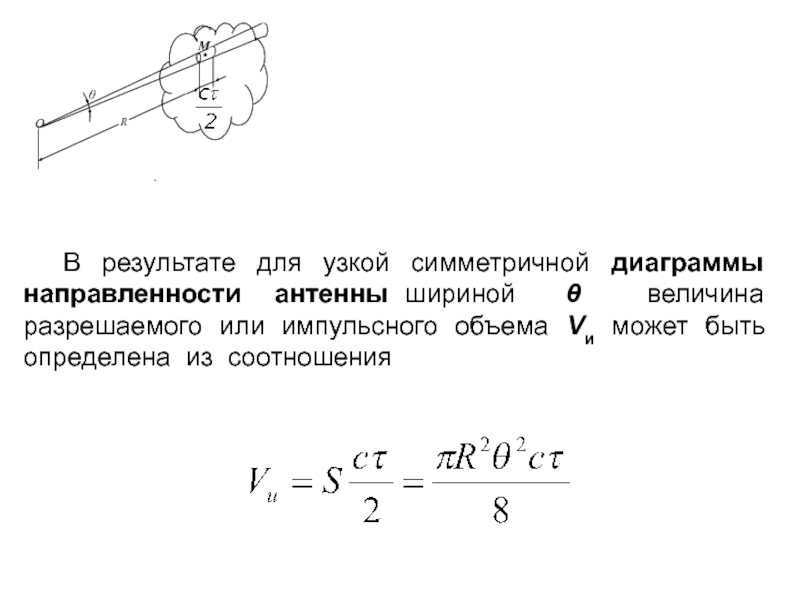
В результате для узкой симметричной диаграммы направленности антенны шириной
величина разрешаемого или импульсного объема Vи может быть
определена из соотношенияСлайд 26 Тогда, в случае релеевского рассеяния для монодисперсных метеорологических объектов их
ЭПР будет описываться следующим выражением:
Слайд 27 Напомним, что ширина угла диаграммы направленности параболических антенн зависит от
диаметра параболического отражателя и длины волны.
Ширина угла диаграммы направленности
(в градусах) определяется соотношениемПри диаметре антенны в 3 м (300 см) и длине волны 3 см ширина диаграммы направленности будет около 0.50.
Слайд 28 Полученные выше выражения для ЭПР справедливы в том случае, когда
разрешаемый объем пространства весь заполнен отражающими частицами.
В реальных
условиях, особенно при наблюдении метеорологических объектов на значительных расстояниях, разрешаемый объем пространства, который увеличивается по мере роста расстояния, может оказаться лишь частично заполненным отражающими частицами.Соответствующее уменьшение ЭПР метеорологического объекта учитывают с помощью коэффициента заполнения: kз ( 0 kз 1).
Слайд 30 Удельная ЭПР метеорологического объекта η при релеевском типе рассеяния
электромагнитной энергии может быть определена из соотношения
Если обозначить
то
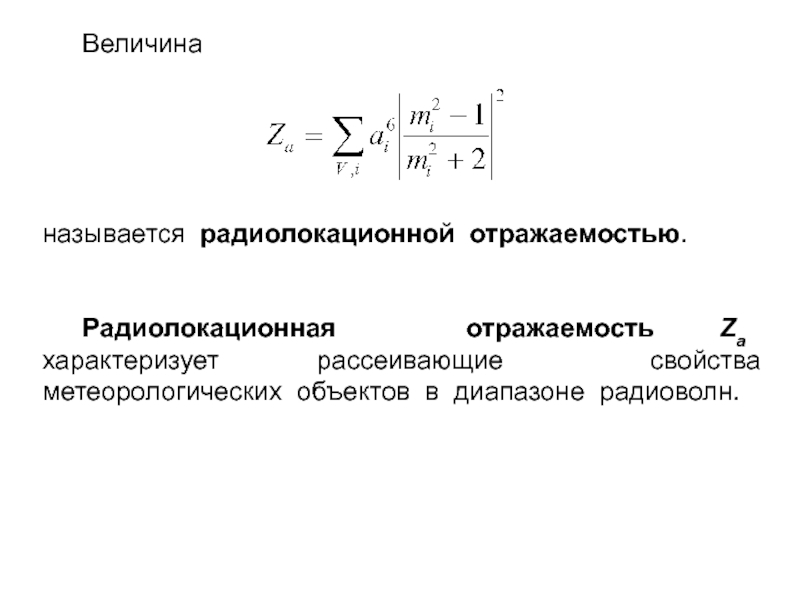
Слайд 31 Величина
называется радиолокационной отражаемостью.
Радиолокационная отражаемость Za характеризует рассеивающие
свойства метеорологических объектов в диапазоне радиоволн.
Слайд 32
Величина радиолокационной отражаемости Zа в отличие от удельной ЭПР
имеет следующие особенности:
- радиолокационная отражаемость метеорологического объекта не зависит
от длины волны ,- радиолокационная отражаемость метеорологического объекта не зависит от каких либо технических характеристик МРЛ, используемой для радиометеорологического зондирования атмосферы.
Слайд 33 Радиолокационная отражаемость Za определяется концентрацией и распределением частиц по размерам
в единичном объеме и их комплексным коэффициентом преломления для используемой
длины волны λ.Если в объеме метеорологического объекта находятся только частицы воды или только частицы льда, радиолокационная отражаемость определяется так:
Для водяных капель и частиц льда
и
Слайд 34
Формулы для Za и выражают еще одну особенность радиометеорологической
информации, а именно - ее сильную зависимость от размеров частиц
в метеорологическом объекте.Из-за этого величины Za и резко возрастают при увеличении размеров частиц и их концентрации в метеорологическом объекте, и резко падают по мере их уменьшения.
Слайд 35
Радиолокационная отражаемость является одной изб основных характеристик, которая измеряется с
помощью МРЛ. Чем она больше, тем точнее и с большего
расстояния она может быть измерена.Отсюда ясно, что радиометеорологический метод зондирования является наиболее эффективным при обнаружении и определении метеорологических объектов, состоящих из большого числа крупных водяных частиц.
Слайд 36 Радиолокационная отражаемость Za является специфической метеорологической характеристикой интегральной микроструктуры
облаков и осадков, такой же как водность облаков W или
интенсивность выпадающих осадков I и содержит метеорологическую информацию об объемах в облаках и осадках, рассеивающих электромагнитное излучение в радиодиапазоне.Слайд 37
Величина радиолокационной отражаемости Za измеряется в м6/м3 или м3.
Однако
для Za удобнее использование размерности мм6/м3, поскольку в этом
случае подчеркивается, что в единице объема (м3) суммируются не просто радиусы находящихся в нем частиц, а радиусы частиц в шестой степени (мм6), соответствующие релеевскому типу рассеяния электромагнитной энергии.Слайд 38
В связи с тем, что диапазон отражаемости Za
для реальных метеорологических объектов может быть очень велик (от 10-5
до 105 мм6/м3), часто для удобства записи Za используют логарифмы или децилогарифмы (lg Za или 10lg Za).Слайд 40 Расчет интенсивности рассеяния электромагнитной энергии объемом, содержащим частички
облаков, требует знания аналитического выражения для функции распределения облачных капель
по размерам (спектра капель).Сложность физических процессов, происходящих в облаках, позволяет говорить только об осредненных спектрах. Причем осреднение должно производиться по большому числу измерений, выполненных в разных облаках и на разных стадиях их развития.
Слайд 41 Функция распределения облачных капель по размерам f(a) описывает зависимость отношения
числа капель Na , радиус которых заключен между a и
a da , к общему числу капель N в некотором объеме воздуха:при условии
Слайд 42 Спектр капель для облаков можно аппроксимировать формулой ХргианаМазина:
где N0
число капель в единице объема, а средний радиус облачных
частиц определяется следующим уравнениемТогда
Последнее уравнение позволяет рассчитать отражаемость облака через средний радиус облачной частицы.
Слайд 43 Для вычисления радиолокационной отражаемости можно использовать такую характеристику как водность
облака W.
Так, для облаков с a < 15 мкм
и W 1.3 г/м3 расчетная формула для Z имеет следующий вид:Приведенные зависимости радиолокационной отражаемости от среднего радиуса облачных частиц и водности облака позволяют при реализации радиометеорологического метода зондирования решать и обратную задачу – по измеренной с помощью МРЛ радиолокационной отражаемости определять среднего радиуса облачных частиц и водности облака.
Слайд 45 Капли мороси и дождя значительно крупнее облачных. Радиус капель мороси
составляет 0.0250.25 мкм.
Радиус наиболее крупных капель дождя может достигать
34 мм; капли дождя большего размера не могут существовать в результате разбрызгивания. Количество капель существенно зависит от интенсивности дождя.
Значительное число дождевых капель имеют сферическую форму, однако, крупные капли дождя приобретают во время падения форму сплюснутых эллипсоидов.
Слайд 46 Функция распределения капель даже для одного облака не является постоянной
и ее изменения, в частности, связаны с изменением физических условий
на пути падения капель.Единственное, что можно с полной уверенностью утверждать относительно спектра капель это то, что этот спектр изменяется во времени и пространстве и, безусловно, зависит от типа облачности, из которой выпадают эти осадки.
Слайд 47 При использовании функции распределения частиц осадков по размерам, предложенной Маршаллом
и Пальмером,
была получена зависимость между Z и I, которая
может быть записана в следующем виде:Z = AI B 220 I B .
Здесь Z отражаемость в мм6/м3, I интенсивность дождя в мм/ч, В – коэффициент, величина которого зависит от многих факторов (сезона, региона, характера осадков: ливинь, морось и т.д.).
Слайд 48 Соотношение,
,
которое иногда называют Z I соотношением, дает достаточно
точную оценку интенсивности осадков до I 25 мм/ч.
При этом коэффициенты A и B зависят от многочисленных факторов (в частности, от типа осадков и особенностей метеорологических процессов в районе наблюдений) и могут изменяться в достаточно широких пределах.
Слайд 50 Для снегопада установлено, что в среднем Z и
I связаны соотношением
где Z в мм6/м3, I
в мм/ч.Поскольку с увеличением интенсивности снегопада меняется его фазовое состояние и происходит нарушение условий релеевского рассеяния, то связь между значениями Z и I может меняться.
Слайд 52 Среднее распределение капель дождя по размерам достаточно удовлетворительно
описывается соотношением
где F(a) характеризует ту часть общего объема
воды, которая приходится на капли радиусом от 0 до a ; параметр, зависящий от интенсивности дождя ( при I= 1 мм/ч =1.3, а при I=25 мм/ч =2.74).Слайд 54
При использовании импульсных РЛС разрешаемый объем метеорологической цели - это
такой объем, от которого одновременно приходит отраженный сигнал. Этот объем
иногда называется импульсным объемом.При длительности формируемого РЛС импульса, равного , занимаемый этим импульсом в пространстве объем в любой момент времени будет равен объему цилиндра с площадью основания S (зависящего от дальности R) и высотой L = с (с – скорость света): V = S L.