Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы зондирования окружающей среды
Содержание
- 1. Методы зондирования окружающей среды
- 2. Радиорефракцией называется искривление траектории распространения электромагнитных волн
- 3. Из-за неоднородности атмосферы как в горизонтальном, так
- 4. Распространение радиоволн в тропосфере
- 5. Тропосфера приземной слой атмосферы от ее
- 6. Основные зависящие от высоты h параметры тропосферы:
- 7. Особенности распространения электромагнитного излучения в неоднородной среде
- 8. Если электромагнитный луч попадает на границу
- 9. Если луч переходит из cреды с большим
- 10. Плотность реальной атмосферы ее плотность убывает с
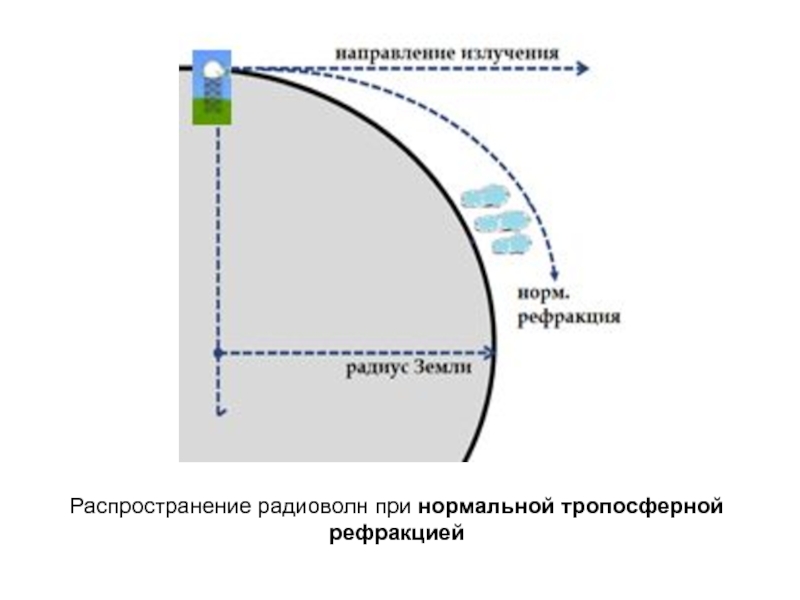
- 11. Распространение радиоволн при нормальной тропосферной рефракцией
- 12. Коэффициент преломления n в тропосфере обычно определяется
- 13. Для характеристики вертикальной изменчивости коэффициента преломления
- 14. Стандартная радиоатмосфера. При радиометеорологическом зондировании атмосферы, а
- 15. Изменение атмосферного давления с высотой определяется барометрическим
- 16. В стандартной радиоатмосфере коэффициент преломления изменяется
- 17. Виды рефракции радиоволн в тропосфере
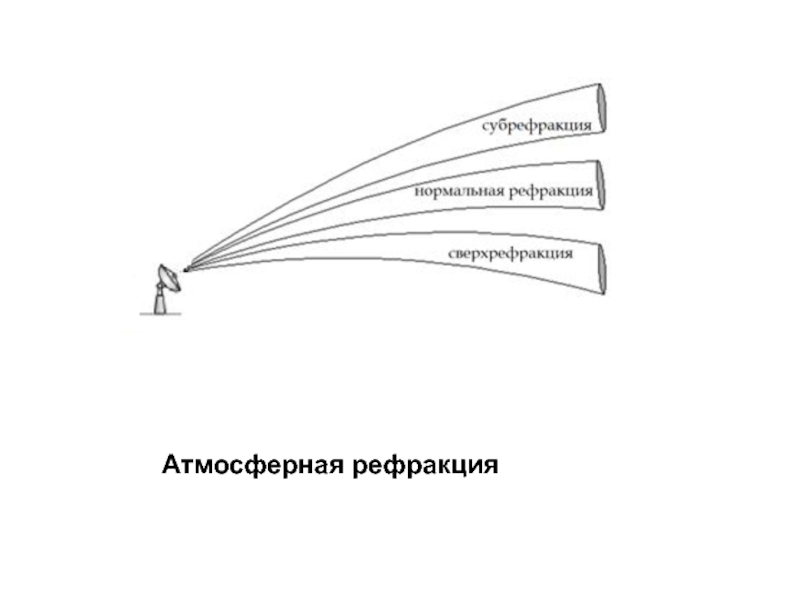
- 18. Схематическое представления видов атмосферной рефракции в тропосфере
- 19. 1. Отрицательная рефракция: на рисунке данная
- 20. 2. Положительная рефракция. Реализуется при В этом
- 21. 2-1. Нормальная рефракция (на рисунке данная траектория
- 22. 2-2. Повышенная рефракция (на рисунке данная траектория
- 23. 2-3. Критическая рефракция (на рисунке данная траектория
- 24. 2-4. Пониженная рефракция (на рисунке данная траектория
- 25. 3. Сверхрефракция (волноводная рефракция) (на рисунке данная
- 26. Количественные характеристики, описывающие радиорефракцию в атмосфере Земли
- 27. 1. Эффективная высота коэффициента преломления
- 28. 2. Радиус кривизны радиолуча в атмосфере Для
- 29. Пусть плоская волна, распространяясь в слое с
- 30. Но Продифференцируем равенство nsin = const :
- 31. Поскольку радиотрассы обычно можно считать пологими, т.
- 32. Если коэффициент преломления меняется с высотой по
- 33. ρ < 0ρ = RЗρ = 4
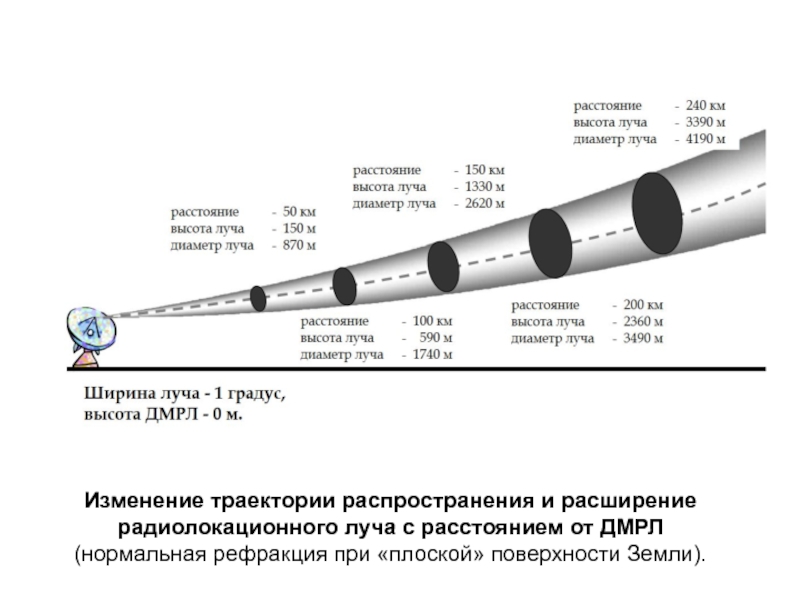
- 34. Законы рефракции в сферической атмосфере Земли
- 35. Если луч падает на границу раздела сферических
- 36. Теорема синусов: для произвольного треугольника выполняется следующее
- 37. Подставляя в соотношениеn1sin 1 = n2sin ’1значение
- 38. Если электромагнитный луч будет распространяться в плоскослоистой
- 39. Когда радиус кривизны радиолуча, направленного вдоль
- 40. Учет явления радиорефракции необходим: -
- 41. Методы учета радиорефракции
- 42. Различают два основных метода учета радиорефракции в
- 43. Метод эквивалентного радиуса Земли
- 44. Метод эквивалентного радиуса сводит задачу
- 45. Определим эквивалентный радиус для случая, когда:
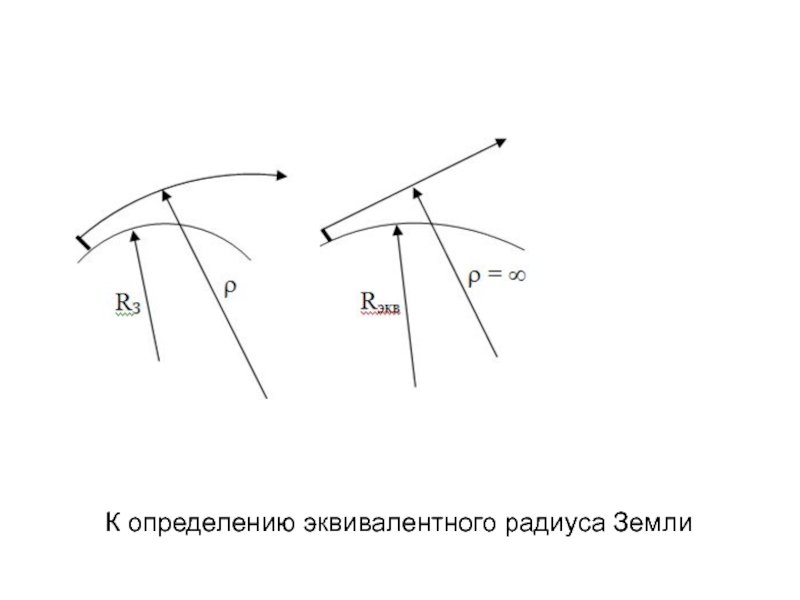
- 46. К определению эквивалентного радиуса Земли
- 47. Для двух точек, одна из которых расположена
- 48. Случай 1: рефракция отсутствует.В этом случае всегда
- 49. Случай 2: присутствует рефракция.В этом случае
- 50. Перепишем последнее соотношение как Теперь учтем (для
- 51. Сравним выражения для sin0 при отсутствии и
- 52. После сравнения двух уравнений можно заметить, что
- 53. Определение дальности радиовидимости при наличии радиорефракции с использованием метода эквивалентного радиуса Земли
- 54. Введенное понятие эквивалентного радиуса позволяет, в частности,
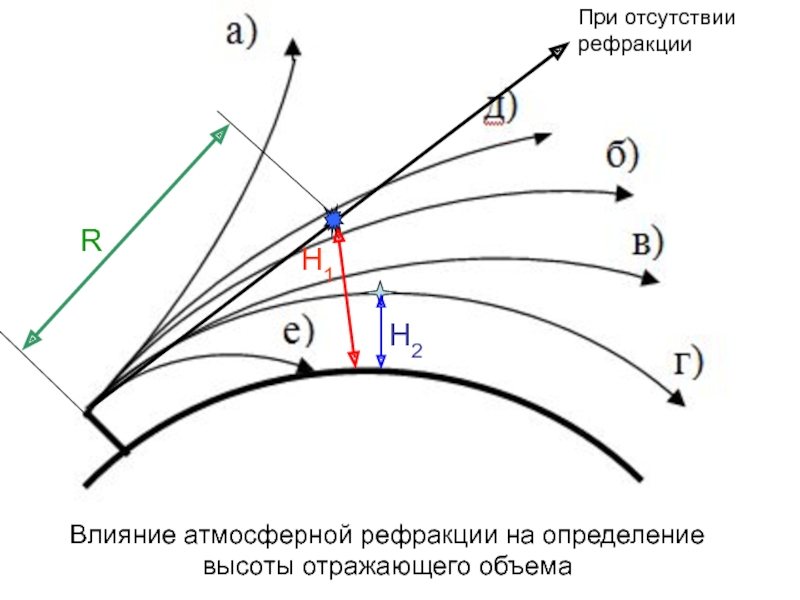
- 55. Определение высоты объектов при использовании для учета радиорефракции метода эквивалентного радиуса Земли
- 56. Реальная высота H объектов в
- 57. Метод приведенного коэффициента преломления
- 58. Использование метода приведенного коэффициента преломления позволяет рассматривать
- 59. С помощью приведенного коэффициента преломления криволинейная
- 60. Для получения аналитического выражения для задания приведенного
- 61. В том случае, если нам удастся свести
- 62. Перепишем это соотношение, разделив левую и правую
- 63. Сравнивая полученное уравнениеn0 sin0 = (n +
- 64. Иными словами, теперь закон распространения будет иметь
- 65. Влияние радиорефракции на работу МРЛ
- 66. Изменение траектории распространения и расширение радиолокационного луча
- 67. Влияние атмосферной рефракции на определение высоты отражающего объемаПри отсутствии рефракцииRH1H2
- 68. Какие будут вопросы ?
- 69. Атмосферная рефракция
- 70. Скачать презентанцию
Радиорефракцией называется искривление траектории распространения электромагнитных волн в атмосфере. Явление радиорефракции связано с изменением показателя преломления электромагнитной волны n в атмосфере.
Слайды и текст этой презентации
Слайд 1Методы зондирования окружающей среды
Профессор Кузнецов Анатолий Дмитриевич
Радиорефракция
Российский государственный гидрометеорологический университет
Слайд 2
Радиорефракцией называется искривление траектории распространения электромагнитных волн в атмосфере.
Явление
Слайд 3 Из-за неоднородности атмосферы как в горизонтальном, так и в вертикальном
направлениях, соответственно указанные искривления траектории могут наблюдаться так же как
в горизонтальной и в вертикальной плоскостях.В земной атмосфере масштабы неоднородностей в горизонтальной и в вертикальной плоскостях значительно отличаются.
Поэтому при рассмотрении радиорефракции обычно учитывается только искривление траектории распространения электромагнитных волн в вертикальной плоскости.
Слайд 5
Тропосфера приземной слой атмосферы от ее поверхности до тропопаузы
(в полярных широтах до 8-10 км в умеренных - до
10-12 км, в тропических - до 16-18 км). В тропосфере сосредоточены более 4/5 всей массы воздуха, почти весь водяной пар, гидрометеоры (жидкие и твердые), в ней возникают самые разнообразные формы облаков и виды осадков.Газовый состав тропосферы постоянен и идентичен составу у поверхности: 78% азота, 21% кислорода, 0,33% аргона, 0,03% CO2 и т. д. Содержание водяного пара от 0 до 4% по объёму.
Слайд 6
Основные зависящие от высоты h параметры тропосферы: p общее
давление, pc давление сухого воздуха, T - абсолютная температура,
e – парциальное давление водяного пара.Температура в тропосфере с высотой h в среднем падает. Верхней границей тропосферы считается высота, на которой падение температуры прекращается (причина роста температуры с уменьшением высоты здесь нагрев поверхности Земли).
Слайд 8 Если электромагнитный луч попадает на границу раздела плоскопараллельных сред
с разными значениями коэффициента n, то искривление траектории
луча будет происходить по законуn1 sin1 = n2 sin2 = … = ni sin i = const.
Слайд 9
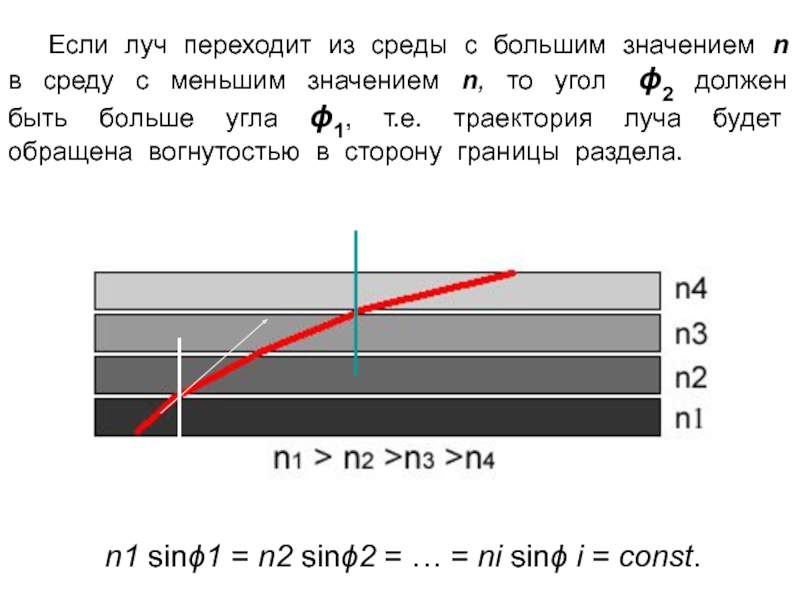
Если луч переходит из cреды с большим значением n в
cреду с меньшим значением n, то угол 2 должен
быть больше угла 1, т.е. траектория луча будет обращена вогнутостью в сторону границы раздела.n1 sin1 = n2 sin2 = … = ni sin i = const.
Слайд 10
Плотность реальной атмосферы ее плотность убывает с высотой.
Поэтому, если
бы коэффициент преломления в земной атмосфере зависел бы только от
плотности, то тогда луч, направленный с земной поверхности вверх, будет переходить из области с большим значением плотности в области с меньшими значениями плотности и, следовательно, всегда отклонялся бы в сторону земной поверхности.Слайд 12
Коэффициент преломления n в тропосфере обычно определяется с помощью полуэмпирической
формулы
Величину N = (n 1)106 называют индексом коэффициента
преломления. Локальные изменения давления, а также температурные инверсии приводят к колебаниям коэффициента преломления вблизи земной поверхности n = 1,00026 1,00046.
Выше 10 км полагают n = сonst = 1,00011.
Слайд 13 Для характеристики вертикальной изменчивости коэффициента преломления атмосферы используют величину
его вертикального градиента.
Вертикальный градиент коэффициента преломления атмосферы может быть определен
с помощью соотношений видаили
где n1 ( N1) и n2 (N2) соответствующие значения коэффициента преломления на высотах нижней и верхней границ рассматриваемого слоя ( h1 и h2).
Слайд 14 Стандартная радиоатмосфера.
При радиометеорологическом зондировании атмосферы, а также при решении
целого ряда других прикладных задач, обычно используются параметры стандартной радиоатмосферной,
максимально приближенные к стандартной атмосфере.В тропосфере для стандартной радиоатмосфере задается линейное уменьшение температуры воздуха с высотой, равное 6.50С на 1 км.
Слайд 15 Изменение атмосферного давления с высотой определяется барометрическим законом
а убывание удельной
влажности воздуха с ростом высоты описывается с помощью следующего эмпирического
соотношенияВ приведенных формулах p0 и q0 давление (гПа) и удельная влажность (г/м3) на нижнем уровне; g ускорение силы тяжести; Т средняя температура столба влажного воздуха от нижнего уровня до уровня h (км); R универсальная газовая постоянная; b и c коэффициенты (0.1112 b 0.2181; 0.0286 c 0.0375).
Слайд 16
В стандартной радиоатмосфере коэффициент преломления изменяется с высотой по
линейному закону и его вертикальный градиент оказывается равным [1/м]
При
отличных от стандартной радиоатмосферы изменения метеорологических величин с высотой в тропосфере можно закон изменения коэффициента преломления с высотой описать зависимостью видагде коэффициент, величина которого может быть определена в соответствии с вертикальным распределением метеорологических величин.
Слайд 18
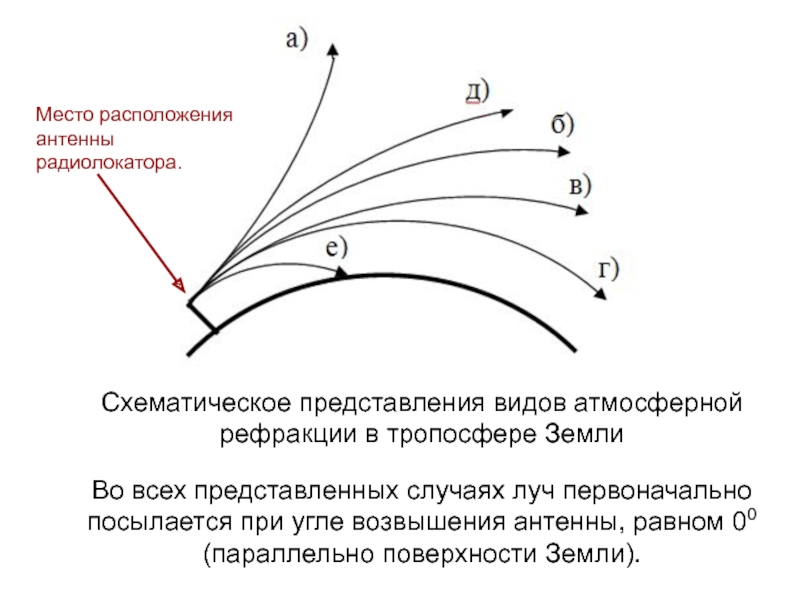
Схематическое представления видов атмосферной рефракции в тропосфере Земли
Во всех представленных
случаях луч первоначально посылается при угле возвышения антенны, равном 00
(параллельно поверхности Земли).Место расположения антенны радиолокатора.
Слайд 19
1. Отрицательная рефракция: на рисунке данная траектория соответствует литере
а. Реализуется при
В этом случае < 0, т. е.
траектория волны направлена выпуклостью вниз. Такой вид рефракции возможен при
Наблюдается в континентальных районах с умеренным климатом, осенью и весной во время утренних туманов.
Слайд 20
2. Положительная рефракция. Реализуется при
В этом случае >
0 и, следовательно, траектория радиолуча обращена выпуклостью вверх.
Различают следующие
частные случаи:- нормальная рефракция (на рисунке данная траектория соответствует литере б);
- повышенная рефракция (на рисунке данная траектория соответствует литере в);
- критическая рефракция (на рисунке данная траектория соответствует литере г);
- пониженная рефракция (на рисунке данная траектория соответствует литере д);
Слайд 21
2-1. Нормальная рефракция (на рисунке данная траектория соответствует литере б).
Реализуется при
При таких средних значениях градиентов температуры и влажнсти
= 4108 м1, Rэкв = 8500 км, = 25000 км.
Наиболее распространённый вид положительной рефракции.
Чаще наблюдается в дневные часы.
Слайд 22
2-2. Повышенная рефракция (на рисунке данная траектория соответствует литере в).
Реализуется при
В этом случае
8500 км
Rэкв < , - 15,7108 м1 < < 4108 м1.
Наблюдается в континентальных районах средних широт в вечерние, ночные и утренние часы летом вследствие температурных инверсий и резкого уменьшения влажности с высотой.
Слайд 23
2-3. Критическая рефракция (на рисунке данная траектория соответствует литере г).
Реализуется при
= 15,7108 м1.В этом случае радиолуч движется параллельно поверхности Земли на постоянной высоте:
Rэкв = , = RЗ.
Наблюдается в континентальных районах средних широт в вечерние, ночные и утренние часы летом вследствие температурных инверсий и резкого уменьшения влажности с высотой;
Слайд 24
2-4. Пониженная рефракция (на рисунке данная траектория соответствует литере д).
Реализуется при
В этом случае
RЗ < Rэкв < 8500 км,
4108 м1 < < 0.
Температура с высотой убывает быстрее, а влажность медленнее, чем при нормальной рефракции.
Обычно наблюдается в пасмурную, дождливую погоду.
Слайд 25
3. Сверхрефракция (волноводная рефракция) (на рисунке данная траектория соответствует литере
е). Реализуется при
При таких градиентах
< - 1/Rэкв, < RЗ, Rэкв < 0. В этом случае волна, отразившись от области высокого градиента, достигает поверхности Земли, отражается от нее, снова преломляется в тропосфере и т. д. Так появляется тропосферный волновод.
Условия появления: резкое понижение n с высотой обычно вследствие температурной инверсии как вблизи поверхности, так и на высотах 2 3 км.
Поскольку температурные инверсии наблюдаются нерегулярно, можно прогнозировать только вероятность появления волновода в определённом районе в определённое время.
Слайд 27 1. Эффективная высота коэффициента преломления
Кроме коэффициента преломления
n и индекса коэффициента преломления N для количественного описания характера
распределения коэффициента преломления с высотой вводят в рассмотрение еще одну характеристику: эффективную высоту коэффициента преломления Hэ.Эффективная высота коэффициента преломления это высота, на которой величина коэффициента преломления уменьшается по сравнению с исходным значением в e раз.
В случае стандартной, или нормальной атмосферы, когда N0 = 25310-6, эффективная высота оказывается равной около 8 км.
Слайд 28
2. Радиус кривизны радиолуча в атмосфере
Для количественного описания траектории
распространения радиолуча в атмосфере при наличии радиорефракции используется такая количественная
характеристика как радиус кривизны радиолуча в атмосфере .Найдём связь между средним градиентом коэффициента преломления в тропосфере и радиусом кривизны радиолуча.
Слайд 29
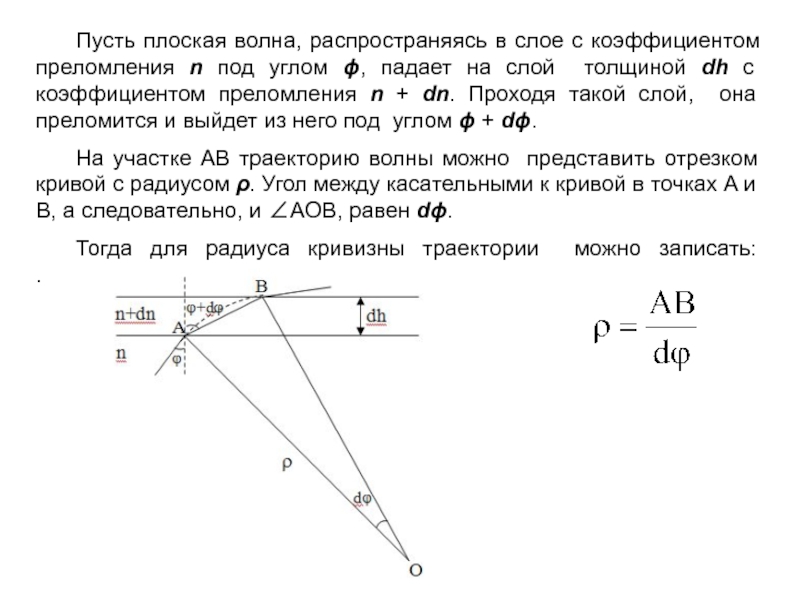
Пусть плоская волна, распространяясь в слое с коэффициентом преломления n
под углом , падает на слой толщиной dh с коэффициентом
преломления n + dn. Проходя такой слой, она преломится и выйдет из него под углом + d.На участке AB траекторию волны можно представить отрезком кривой с радиусом . Угол между касательными к кривой в точках A и B, а следовательно, и AOB, равен d.
Тогда для радиуса кривизны траектории можно записать: .
Слайд 30
Но
Продифференцируем равенство
nsin = const :
d(nsin =
const) = sin dn+ n cos d = 0,
Из последних двух равенств после их подстановки в формулу для радиуса кривизны траектории получаем
Слайд 31
Поскольку радиотрассы обычно можно считать пологими, т. е.
sin
1,
и, кроме того, в тропосфере
n 1,
окончательно
получаем Слайд 32 Если коэффициент преломления меняется с высотой по линейному закону, то
радиус кривизны траектории с высотой не меняется, т. е. имеем
распространение по дуге окружности.Для модели нормальной тропосферы
м1 ,
следовательно, 25000 км 4 RЗ.
Напомним, что распространение радиоволн по дуге круга такого радиуса называется нормальной тропосферной рефракцией.
Слайд 33
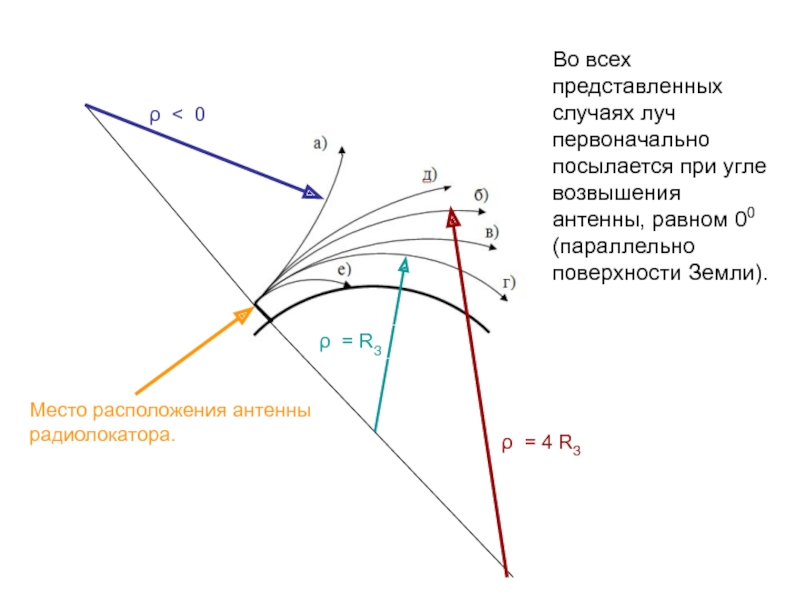
ρ < 0
ρ = RЗ
ρ = 4 RЗ
Место расположения антенны
радиолокатора.
Во всех представленных случаях луч первоначально посылается при угле
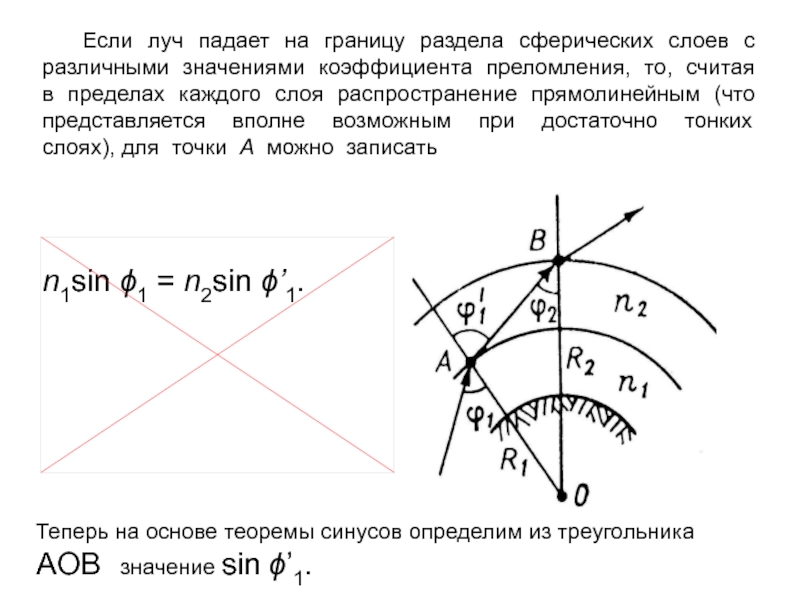
возвышения антенны, равном 00 (параллельно поверхности Земли). Слайд 35 Если луч падает на границу раздела сферических слоев с различными
значениями коэффициента преломления, то, считая в пределах каждого слоя распространение
прямолинейным (что представляется вполне возможным при достаточно тонких слоях), для точки A можно записатьn1sin 1 = n2sin ’1.
Теперь на основе теоремы синусов определим из треугольника AOB значение sin ’1.
Слайд 36
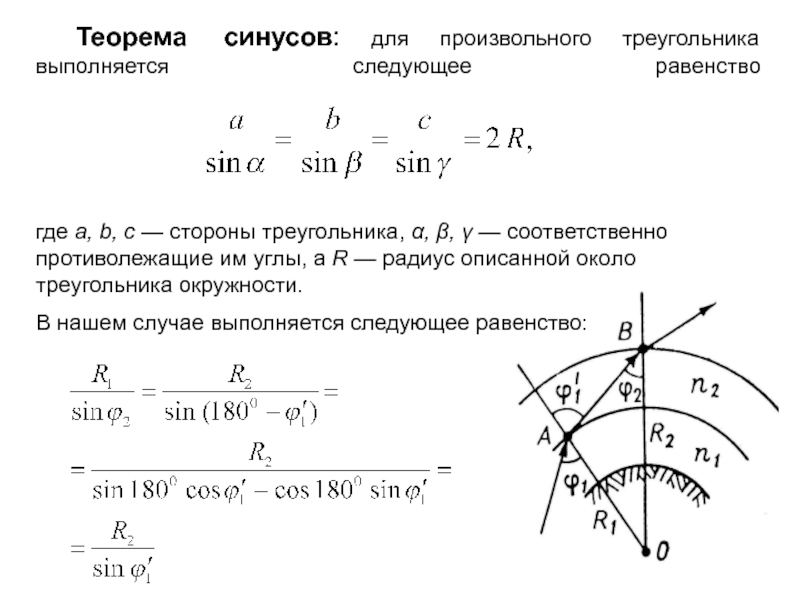
Теорема синусов: для произвольного треугольника
выполняется следующее равенство
где a, b, c
— стороны треугольника, α, β, γ — соответственно противолежащие им
углы, а R — радиус описанной около треугольника окружности.В нашем случае выполняется следующее равенство:
Слайд 37
Подставляя в соотношение
n1sin 1 = n2sin ’1
значение n2sin ’1 из
соотношения
получаем
n1 R1 sin1 = n2 R2 sin2
Или, в общем случае
n
R sin = const. Слайд 38 Если электромагнитный луч будет распространяться в плоскослоистой атмосфере, в которой
коэффициент преломления изменяется постепенно, то будет происходить плавное искривление
траектории луча.Как уже было показано ранее, радиус кривизны радиолуча в атмосфере определяется величиной градиента коэффициента преломления в соответствии с выражением
где dn/dh вертикальный градиент коэффициента преломления.
Слайд 39 Когда радиус кривизны радиолуча, направленного вдоль земной поверхности, равен
радиусу кривизны земной поверхности, луч огибает земной шар.
Такая рефракция называется критической рефракцией.Условием критической рефракции будет
где [dn/dh] = 1/м , Rз радиус Земли.
Слайд 40 Учет явления радиорефракции необходим:
- при определении высоты
объектов над земной поверхностью, измеренной радиолокационным методом;
- при
определении предельной дальности обнаружения метеообьектов.Слайд 42
Различают два основных метода учета радиорефракции в атмосфере:
- метод
эквивалентного радиуса Земли;
- метод приведенного коэффициента преломления.
Слайд 44 Метод эквивалентного радиуса сводит задачу криволинейного распространения радиоволн
к задаче с прямолинейным распространением.
Для этого криволинейную траекторию луча
как бы “разгибают”, изменяя радиус Земли до тех пор, пока траектория луча не станет прямолинейной.Полученный таким образом радиус сферы называют эквивалентным радиусом Земли Rэ.
Слайд 45
Определим эквивалентный радиус для случая, когда:
- вертикальный градиент
коэффициента преломления постоянен,
- луч первоначально направлен под углом
0 к вертикали. Слайд 47 Для двух точек, одна из которых расположена на земной поверхности,
а вторая на высоте H, на основании соотношения
n
R sin = constможно записать
n0 Rз sin 0 = n (Rз + H) sin ,
где n0 и n значения коэффициента преломления на уровне земной поверхности и на высоте H соответственно.
Из последнего выражения выразим значение sin0 для двух случаев: при отсутствии рефракции и при ее наличии.
Слайд 48
Случай 1: рефракция отсутствует.
В этом случае всегда n = n0
и из уравнения
n0 Rз sin0 = n0 (Rз +
H) sinполучаем
Rз sin0 = Rз sin + H sin
Или
sin0 = [1 + H/ Rз ] sin
Слайд 49
Случай 2: присутствует рефракция.
В этом случае n ≠ n0
и значение коэффициента преломления атмосферы на высоте H связано с
его приземным значением n0 соотношением (линейное приближение)Поэтому соотношение
n0 Rз sin0 = n (Rз + H) sin
может быть теперь
Слайд 50Перепишем последнее соотношение как
Теперь учтем (для пренебрежения последним слагаемым
в скобках), что
Теперь для учета радиорефракции получаем следующее приближенное выражение
Слайд 51
Сравним выражения для sin0 при отсутствии и наличии рефракции (для
случаев 1 и 2):
- случай 1
sin0 =
[1 + H(1/ Rз )] sin- случай 2
Слайд 52
После сравнения двух уравнений можно заметить, что они совпадают друг
с другом при условии, что в последнем уравнение вмести Rз
следует подставить так называемый эквивалентный радиус Rэ (учитывающий наличие градиента коэффициента преломления)Последнее уравнение и есть определение эффективного радиуса Rэ.
Тогда
Слайд 53
Определение
дальности радиовидимости
при наличии радиорефракции
с использованием
метода эквивалентного
радиуса Земли
Слайд 54 Введенное понятие эквивалентного радиуса позволяет, в частности, определить дальность
радиовидимости Rпр , т.е. такое расстояние до объекта, при
котором еще возможно его «визуальное» обнаружение (объект не находится в зоне радиотени).Для нулевых углов возвышения Rпр определяется следующим выражением
где h высота антенны радиолокатора над поверхностью, H – высота объекта над поверхностью.
В условиях нормальной рефракции Rэ=8548 км и
Слайд 55
Определение
высоты объектов
при использовании для учета радиорефракции метода эквивалентного
радиуса Земли
Слайд 56 Реальная высота H объектов в атмосфере может быть
найдена только путем введения соответствующей поправки на радиорефракцию, зависящей от
вертикального угол радиолуча и расстояния до объекта.С учетом рефракции реальная высота объекта H определяется по следующей формуле
H = L sin + L2 + h,
где h – высота антенны радиолокатора над поверхностью, L расстояние до объекта, вертикальный угол радиолуча, коэффициент, который для условий нормальной рефракции равен 610-5 км-1.
Слайд 58 Использование метода приведенного коэффициента преломления позволяет рассматривать распространение луча над
плоской поверхностью.
При этом влияние кривизны земной поверхности и кривизны
сферической слоистой атмосферы учитываются за счет введения дополнительного значения коэффициента преломления атмосферы: Δn. Таким образом, задача построения траектории луча сводится к построению траектории над плоской поверхностью при для профиля приведенного коэффициента преломления nприв(H) = n(H) + Δn(H),
где H – высота.
Слайд 59
С помощью приведенного коэффициента преломления криволинейная траектория луча вместе
с земной поверхностью «разгибается» до тех пор, пока сферическая поверхность
Земли не превратиться в плоскую. При этом луч будет иметь другую, по сравнению со сферической атмосферой, кривизну и его новая траектория как раз и будет определяться приведенным коэффициентом преломления.Слайд 60 Для получения аналитического выражения для задания приведенного коэффициента преломления вспомним,
что для плоскопараллельной неоднородной атмосферы выполняется соотношение
n sin = const,
а для сферической неоднородной атмосферы
n R sin = const.
Слайд 61
В том случае, если нам удастся свести последнее соотношение к
случаю плоскопараллельной атмосферы (убрав зависимость от R), мы и получим
метод приведенного коэффициента преломления.Для этого снова обратимся к соотношению для сферической атмосферы для двух точек, одна из которых расположена на земной поверхности, а вторая на высоте H
n0 Rз sin0 = n (Rз + H) sin ,
где n0 и n значения коэффициента преломления на уровне земной поверхности и на высоте H соответственно.
Слайд 62 Перепишем это соотношение, разделив левую и правую его части на
Rз:
n0 sin0 = (n Rз / Rз + n H/
Rз) sin .Учтем, что n ≈ 1. Тогда
n Rз / Rз ≈ n, и n H/ Rз ≈ H/ Rз .
Отсюда получаем, что для любой высоты H
n0 sin0 = (n + H/ Rз) sin .
Слайд 63 Сравнивая полученное уравнение
n0 sin0 = (n + H/ Rз) sin
с
уравнением
n sin = const
можно рассматривать распространение луча уже над плоской
поверхностью, но при условии, что коэффициент преломления на каждой высоте H имеет значение не n, а дополнительное значение коэффициента преломления атмосферы:Δn = H/ Rз
Слайд 64 Иными словами, теперь закон распространения будет иметь следующий вид (рефракция
над плоской поверхностью):
nприв sin = const,
где для любой высоты H
при расчете траектории распространения вместо истинного значения коэффициента преломления n следует использовать его приведенное значение nприв :nприв = n + H/ Rз .



































































![АВТОМАТИЗАЦИЯ ЗВУКА [ Л ]
В СЛОВАХ](/img/tmb/6/598195/9904114927fd66f267234b3a5c44ea6c-800x.jpg)