Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МКХА
Содержание
- 1. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МКХА
- 2. Метрологические характеристики МКХАТОЧНОСТЬ ИЗМЕРЕНИЙДОСТОВЕРНОСТЬ ИЗМЕРЕНИЙПравильность результатов измеренияПрецизионность результатов измеренияПовторяемость результатов измеренияВоспроизводимость результатов измерения
- 3. Образцы для оценивания (ОО) показателей качества МКХАСтандартный
- 4. Точность измерений Характеристика качества измерений, отражающая близость
- 5. Точность методики анализа
- 6. Правильность Характеризует степень близости среднего арифметического значения
- 7. Систематическая погрешность — это составляющая погрешности измерения,
- 8. При оценки правильности в качестве истинного значения
- 9. Правильность методики анализа
- 10. Прецизионность результатов измерений – степень близости друг
- 11. Повторяемость
- 12. − Воспроизводимость результатов измерений (воспроизводимость измерений) -
- 13. Случайные погрешности являются следствием многих причин, предусмотреть
- 14. Плотность нормального распределения для случайной величины Х описывается уравнением:
- 15. Дисперсия является мерой рассеивания, имеет размерность квадрата
- 16. Воспроизводимость
- 17. Слайд 17
- 18. ОЦЕНКА ПОКАЗАТЕЛЕЙКАЧЕСТВА МКХА
- 19. 1. Оценка показателей прецизионности МКХА
- 20. n – число параллельных определений;m – количество образцов;l - число лабораторий (лаборантов)
- 21. 1.1. Повторяемость
- 22. 1. Среднее арифметическое значение величины Хml
- 23. 3. Проверка гипотезы о равенстве генеральных
- 24. Слайд 24
- 25. Слайд 25
- 26. ПримерРезультаты определения никеля в стандартном образце сплава,
- 27. ПримерРезультаты определения никеля в стандартном образце сплава,
- 28. Критерий Кохрена Gтабл = 0,544. Gm(max) ≤
- 29. 1.2. Воспроизводимость
- 30. 1.2. Воспроизводимость
- 31. среднее значение результатов анализа
- 32. Слайд 32
- 33. •• определяют табличное значение GRтабл для
- 34. • сравнивают расчетные значения с табличными
- 35. выборочное СКО результатов анализа
- 36. Предел повторяемости (rnm)
- 37. п — число параллельных определений, предусмотренных МКХАQ(P,
- 38. СКО результатов анализаКритерий Граббса Grтабл = 1,481GRmax ≤ GRтабл и GRmin ≤ GRтабл
- 39. Выборочное СКО результатов анализа
- 40. 2. Оценка правильности МКХА
- 41. Правильность методики анализа
- 42. Границы (c.н, c.в) систематической погрешности методики анализпредставляет
- 43. математическое ожидание систематической погрешности методики анализа (m
- 44. проверка значимость вычисленных значений m по критерию
- 45. Если tm > tтабл, то оценка систематической
- 46. Продолжение примераМатематическое ожидание систематической погрешности методики анализа
- 47. 3. Оценка точности МКХА
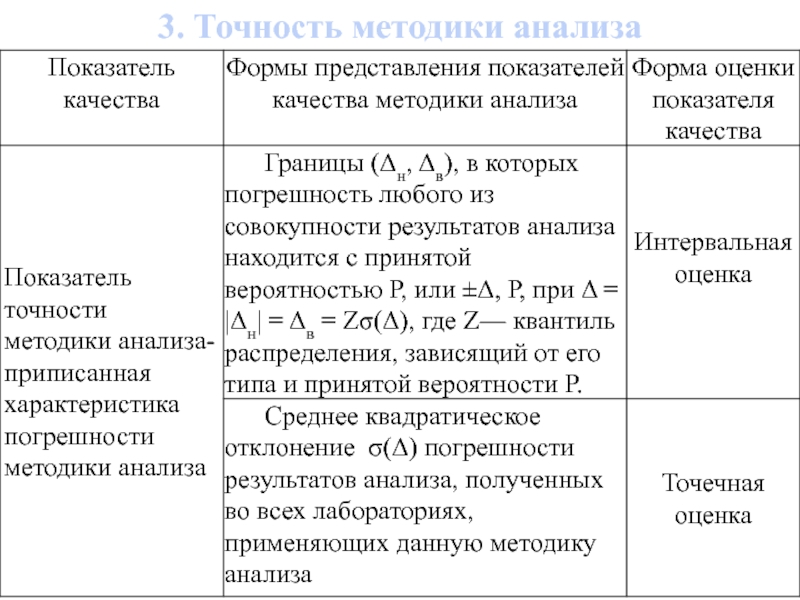
- 48. 3. Точность методики анализа
- 49. Верхнюю (в т) и нижнюю (н т)
- 50. Продолжение примераВерхняя (в т) и нижняя (н
- 51. ПРОВЕРКА ПРИЕМЛЕМОСТИ РЕЗУЛЬТАТОВ КХАМИ 2881-2004. Методики количественного химического анализа. Процедуры проверки приемлемости результатов анализа
- 52. Если документом на МКХА предусмотрено проведение параллельных
- 53. Проверка приемлемости результатов единичных анализов, полученных в
- 54. 3. Сравнивают абсолютное расхождение (rk) с пределом
- 55. При невыполнении условия (18) может быть принято
- 56. За результат анализа принимают среднее арифметическое из
- 57. Пример 2. Определение массовой доли кремния в
- 58. Решение1. Абсолютное расхождение между максимальным и минимальным
- 59. Слайд 59
- 60. Проверка приемлемости результатов анализа, полученных в условиях воспроизводимости
- 61. При выполнении условия в качестве окончательного результата
- 62. Слайд 62
- 63. Слайд 63
- 64. НЕОПРЕДЕЛЕННОСТЬ РЕЗУЛЬТАТОВ КХАНеопределенность u - параметр, связанный
- 65. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Метрологические характеристики МКХА
ТОЧНОСТЬ ИЗМЕРЕНИЙ
ДОСТОВЕРНОСТЬ ИЗМЕРЕНИЙ
Правильность результатов измерения
Прецизионность результатов измерения
Повторяемость результатов
измерения
Слайд 3Образцы для оценивания (ОО) показателей качества МКХА
Стандартный образец (СО);
Аттестованная
смесь (АС).
Аттестованная смесь - смесь двух и более веществ (материалов),
имеющая нормированные метрологические характеристики, устанавливаемые методом аттестации по процедуре приготовления, и создаваемая на месте применения в соответствии с регламентированной и утвержденной методикой
Слайд 4Точность измерений
Характеристика качества измерений, отражающая близость к нулю погрешности
его результата
Чем меньше результат измерения отклоняется от истинного значения
величины, то есть чем меньше его погрешность, тем выше точность измерения, независимо от того, является ли погрешность систематической, случайной или содержит ту и другую составляющиеСлайд 6Правильность
Характеризует степень близости среднего арифметического значения большого числа результатов
измерений к истинному значению и оценивается смещением среднего арифметического значения
при многократных измерениях ФВ от истинного значенияПоказателем правильности измерений является значение систематической погрешности.
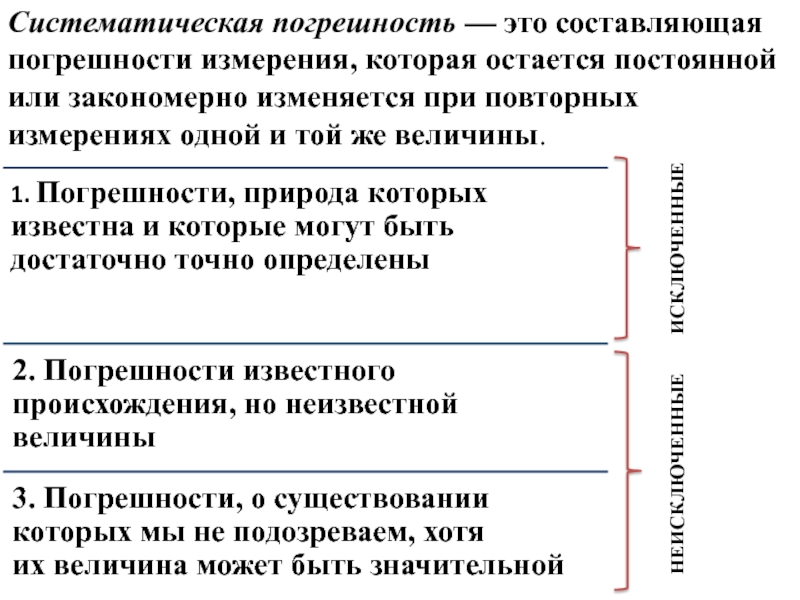
Слайд 7Систематическая погрешность — это составляющая погрешности измерения, которая остается постоянной
или закономерно изменяется при повторных измерениях одной и той же
величины.ИСКЛЮЧЕННЫЕ
НЕИСКЛЮЧЕННЫЕ
Слайд 8При оценки правильности в качестве истинного значения используют опорное значение,
т.е. значение, которое служит в качестве согласованного для сравнения:
теоретическое
или установленное значение, базирующееся на научных принципах;приписанное или аттестованное значение, базирующееся на экспериментальных работах;
математическое ожидание измеряемой характеристики, т. е. среднее значение заданной совокупности результатов измерений
Слайд 10Прецизионность результатов измерений –
степень близости друг к другу независимых
результатов измерений, полученных в конкретных регламентированных условиях.
Прецизионность зависит только
от случайных погрешностей− Повторяемость результатов измерений (сходимость измерений) - это близость друг к другу результатов измерений одной и той же величины, выполненных несколько раз одними и теми же СИ, одним и тем же методом, одним и тем же оператором в одинаковых условиях и с одинаковой тщательностью
Слайд 12− Воспроизводимость результатов измерений (воспроизводимость измерений) - это близость результатов
измерений одной и той же величины, полученных в различных местах,
разными СИ, разными операторами, в разное время, но приведенных по одной методике в одних и тех же условиях измерений (температуре, давлению, влажности и др.)Воспроизводимость и сходимость оцениваются средними квадратическими погрешностями результатов измерений.
Слайд 13Случайные погрешности являются следствием многих причин, предусмотреть влияние которых при
данном измерении оказывается невозможным.
Оценку случайных погрешностей производят с помощью
математической статистики по результатам многократных измерений.Большинство встречающихся на практике случайных величин, в том числе случайные погрешности измерений, распределено по нормальному закону (закону Гаусса).
Слайд 15Дисперсия является мерой рассеивания, имеет размерность квадрата измеряемой физической величины.
С точки зрения размерности она не совсем удобна в качестве
характеристики рассеивания (а значит и случайной погрешности).На практике чаще используют положительное значение корня квадратного из дисперсии — среднее квадратическое отклонение (СКО) результатов наблюдений:
Слайд 20n – число параллельных определений;
m – количество образцов;
l - число
лабораторий (лаборантов)
Слайд 221. Среднее арифметическое значение величины Хml
(1)
2. Дисперсия результатов единичного анализа содержания компонента в т-м образце, полученных в условиях повторяемости (параллельных определений)
(2)
Порядок расчета СКО результатов единичного анализа, r.
Слайд 23 3. Проверка гипотезы о равенстве генеральных дисперсий по критерию
Кохрена Gm(max)
Критерий Кохрена рассчитывают по формуле
(S2ml)max – максимальная дисперсия.
•
Находят табличное значение Gтабл при числе степеней свободы v = N – 1 и f = L.Слайд 26Пример
Результаты определения никеля в стандартном образце сплава, полученные в условиях
повторяемости и воспроизводимости представлены в таблице. Содержание никеля согласно паспорту
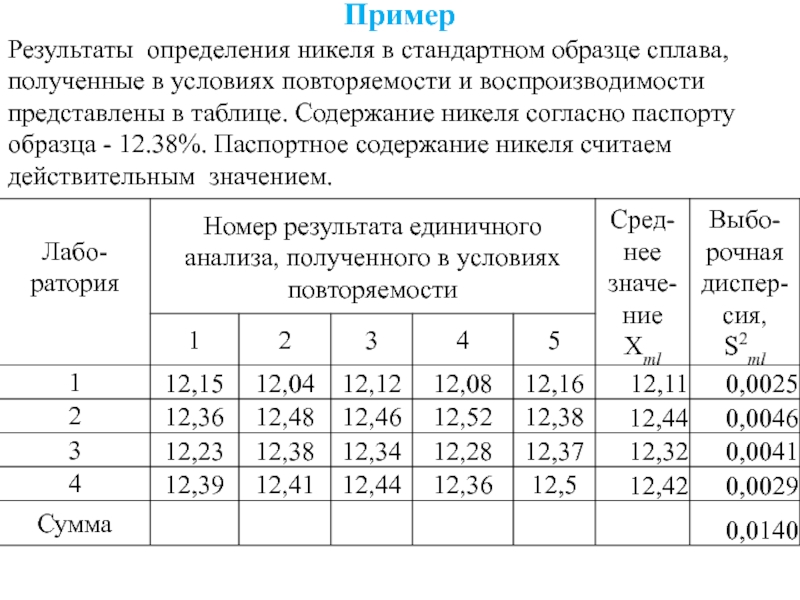
образца - 12.38%. Паспортное содержание никеля считаем действительным значением.Слайд 27Пример
Результаты определения никеля в стандартном образце сплава, полученные в условиях
повторяемости и воспроизводимости представлены в таблице. Содержание никеля согласно паспорту
образца - 12.38%. Паспортное содержание никеля считаем действительным значением.Слайд 28Критерий Кохрена
Gтабл = 0,544. Gm(max) ≤ Gтабл гипотеза о
равенстве генеральных дисперсий принимается.
СКО (Srm) , характеризующие повторяемость результатов единичного
анализаСлайд 31 среднее значение результатов анализа Хm, полученных
в условиях воспроизводимости
(6)СКО Sm результатов анализа:
Порядок расчета σR
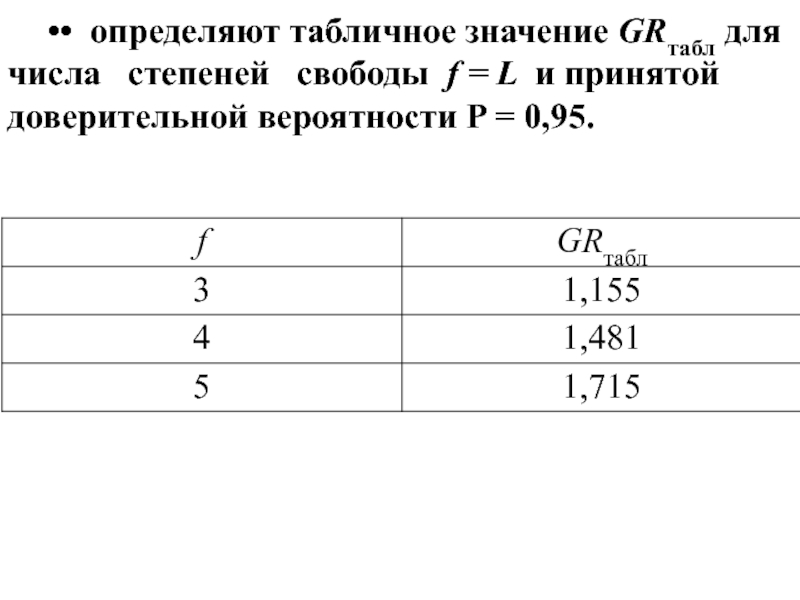
Слайд 33•• определяют табличное значение GRтабл для числа степеней
свободы f = L и принятой доверительной вероятности P
= 0,95.Слайд 34• сравнивают расчетные значения с табличными значением GRm,max
и GRm,min с табличным значением GRтабл
Если GRm,max > GRтабл или/и
GRm,min > GRтабл, то соответствующие результаты Xm,max или/и Xm,min из дальнейших расчетов исключают. Проверку по критерию Граббса продолжают до тех пор, пока не будут выполнены условия:
GRm,max ≤ GRтабл и GRm,min ≤ GRтабл
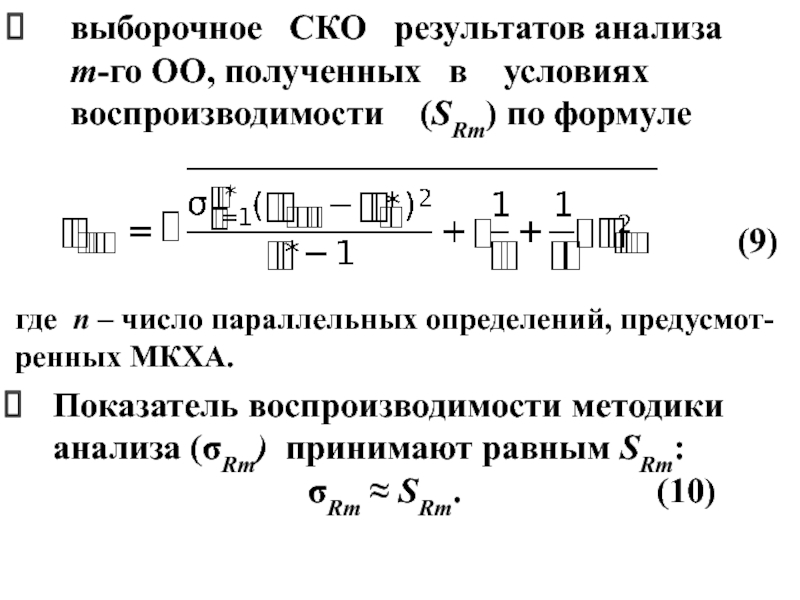
Слайд 35выборочное СКО результатов анализа m-го ОО, полученных
в условиях воспроизводимости (SRm) по формуле
(9)где п – число параллельных определений, предусмот-ренных МКХА.
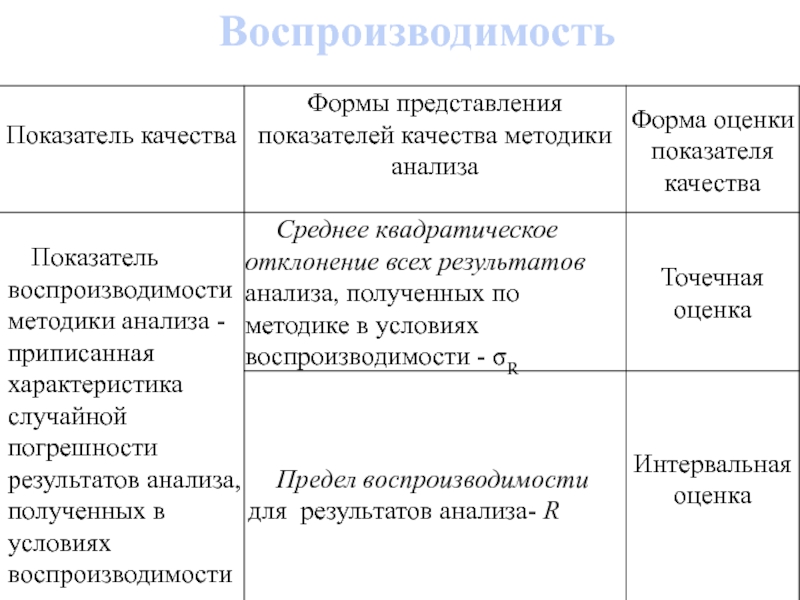
Показатель воспроизводимости методики анализа (Rm) принимают равным SRm:
Rm SRm. (10)
Слайд 36 Предел повторяемости (rnm) и предел воспроизводимости
(Rm) - расхождения между результатами измерений в соответствующих условиях.
Предел повторяемости
(rnm) для содержания, соответствующего содержанию компонента в m-м ОО, рассчитывают по формулеrnm = Q(P, n)rm, (11)
Предел воспроизводимости (Rm) для содержания, соответствующего содержанию компонента в m-м OO, рассчитывают по формуле
Rm = Q(P, l)Rm. (12)
Слайд 37п — число параллельных определений, предусмотренных МКХА
Q(P, n) = 2,77
при n = 2, Р = 0,95;
Q(P, n) = 3,31
при п = 3, Р = 0,95;Q(P, n) = 3,63 при п = 4, Р = 0,95;
Q(P, n) = 3,86 при п = 5, Р = 0,95.
Слайд 39Выборочное СКО результатов анализа по уравнению (8)
при n=2, N=5
SR = 0,159
Показатель воспроизводимости методики анализа
Rm SRm=
0,159Предел повторяемости
r = Q(P, n)r = 0,16
Предел воспроизводимости
R = Q(P, l)R= 0,44
Q(P, n) = 2,77 при п = 2 (l =2 ), Р = 0,95
Слайд 42Границы (c.н, c.в) систематической погрешности методики анализ
представляет собой верхнюю (с.в
m) и нижнюю (с.н m) границы, в которых неисключенная систематическая
погрешность методики анализа для содержания, соответствующего содержанию компонента в m-м ОО, находится с принятой вероятностью Р= 0,95Слайд 43математическое ожидание систематической погрешности методики анализа (m ) - разность
между средним значением результатов анализа Хm и аттестованным значением m-го
OO (Cт)т = Хm - Cm, (13)
т = 1, ..., М.
дисперсия средних арифметических значений результатов единичного анализа Хml относительно среднего значения результатов анализа Хm
(14)
Порядок расчета
Слайд 44проверка значимость вычисленных значений m по критерию Стьюдента (tm)
(15)
Δоm - погрешность аттестованного значения m-го OO.
Полученное значение tm сравнивают с tтабл при числе степеней свободы f = L - 1 для доверительной вероятности Р = 0,95.
Слайд 45Если tm > tтабл, то оценка систематической погрешности значима на
фоне случайного разброса.
Принимаемые решения
введении поправки в
результаты анализадоработка методики.
Если tm tтабл, то оценка систематической погрешности незначима на фоне случайного разброса, и в этом случае ее принимают равной нулю (m = 0).
Слайд 46Продолжение примера
Математическое ожидание систематической погрешности методики анализа
= Х -
C =12,38 -12,323 = 0,058
Дисперсия средних арифметических значений результатов единичного
анализа Х l относительно среднего значения результатов анализа Х S2=0,23Критерий Стьюдента
t = 0,851; tтаб = 3,18; tm tтабл, т.е. = 0.
Отличие результата анализа от действительного значения незначимо, методика не содержит систематической погрешности Границы (c.н, c.в) систематической погрешности методики анализ (уравнение 16)
c.в = |c.н| = с = 0,148
Слайд 49Верхнюю (в т) и нижнюю (н т) границы, в которых
погрешность результата анализа (для содержания, соответствующего содержанию определяемого компонента в
m-м ОО) находится с принятой вероятностью Р = 0,95, рассчитывают по формуле(17)
в = |н| = = 0,332=0,3
Результат измерения:
Х = (2,318 ± 0,332) %= (2,3 ± 0,3) %
Паспортное содержание никеля попадает в доверительный интервал
Продолжение примера
Слайд 50Продолжение примера
Верхняя (в т) и нижняя (н т) границы погрешности
в
= |н| = = 0,332 ≈ 0,3
Слайд 51 ПРОВЕРКА ПРИЕМЛЕМОСТИ РЕЗУЛЬТАТОВ КХА
МИ 2881-2004. Методики количественного химического анализа.
Процедуры проверки приемлемости результатов анализа
Слайд 52Если документом на МКХА предусмотрено проведение параллельных определений, то проверку
приемлемости результатов анализа, полученных в условиях повторяемости, осуществляют при получении
каждого результата анализа рабочих проб.Процедуры проверки приемлемости результатов анализа, полученных в условиях воспроизводимости, могут быть приведены в документе на МКХА, в соглашении между поставщиком и потребителем и т.п.
Слайд 53Проверка приемлемости результатов единичных анализов, полученных в условиях повторяемости
1. Рассчитывают абсолютное расхождение (rk) между наибольшим Хmax,n
и наименьшим Xmin,n из n регламентированных в МКХА результатов единичного анализа, выполненных для получения результата анализа.2. В МКХА находят значение предела повторяемости (r).
Слайд 543. Сравнивают абсолютное расхождение (rk) с пределом повторяемости (r).
Результаты КХА
считаются приемлемыми, если выполнено условие
rk ≤ r.
(18) За результат анализа принимают среднее арифметическое из n результатов единичного анализа Xi, i =1, ..., n:
Слайд 55При невыполнении условия (18) может быть принято одно из следующих
решений :
Отказ от полученных результатов единичного анализа и проведение повторного
анализа рабочей пробы.Проведение дополнительных т параллельных определений, при этом m = n, если процедура получения результатов единичного анализа не является дорогостоящей; m = 1, если процедура является дорогостоящей.
Слайд 56За результат анализа принимают среднее арифметическое из n + m
результатов единичного анализа при выполнении условия
rk' = Xmax,n+m - Xmin,n+m
≤ CR0,95(n + m),где Xmax,n+m - максимальный из n + m результатов единичного анализа;
Xmin,n+m - минимальный из n + m результатов единичного анализа;
CR0,95(n + m) - значение критического диапазона для числа результатов единичного анализа n + m.
CR0,95(n + m) = Q(P; n') · σr
где n' = n + m;
σr - СКО повторяемости, установленное в МКХА
Слайд 57Пример 2.
Определение массовой доли кремния в пробах технического алюминия
спектральным методом
Процедура анализа не является дорогостоящей.
Исходные данные:
- n
= 2;- предел повторяемости r = 0,17.
В условиях повторяемости получены следующие результаты единичного анализа:
X1 = 5,74 % и Х2 = 5,56 %.
Слайд 58Решение
1. Абсолютное расхождение между максимальным и минимальным результатами единичного анализа
рассчитывают по формуле
rk = 5,74 - 5,56 = 0,18 %
2.
Фактическое значение абсолютного расхождения результатов единичного анализа превышает значение предела повторяемости:rk > rn.
3. Дополнительно получают два результата единичного анализа: Х3 = 5,63 % и Х4 = 5,68 %.
4. Значение критического диапазона:
CR0,95(4) = Q(0,95; 4) · σr = 3,63 · 0,06 = 0,22 %
Слайд 61При выполнении условия в качестве окончательного результата анализа используют общее
среднее значение результатов анализа, полученных в двух лабораториях.
Если представленные каждой
из двух лабораторий результаты анализа получены в точном соответствии с МКХА, то критическая разность является пределом воспроизводимости и его значение может быть рассчитано по формулеR = CD0,95 = 2,77σR.
Слайд 64 НЕОПРЕДЕЛЕННОСТЬ РЕЗУЛЬТАТОВ КХА
Неопределенность u - параметр, связанный с результатом измерения,
который характеризует дисперсию значений, которые могли быть приписаны измеряемой величине
Для
характеристики неопределенности используются стандартное отклонение или ширина доверительного интервалаКоличественно характеристики погрешности измерений и соответствующие виды неопределенности измерений совпадают.