Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ
Содержание
- 1. МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ
- 2. 1.Понятие о минимизации ПФПри технической реализации переключательных
- 3. 1.Понятие о минимизации ПФОграничимся целью нахождения наиболее
- 4. 1.Понятие о минимизации ПФМетоды минимизации разрабатываются применительно
- 5. Импликанта и имплицентаПри минимизации переключательных функций существенную
- 6. ИмпликантаПереключательная функция g(х) называется импликантой переключательной функции
- 7. ИмплицентаПереключательная функция р(х) является имплицентой переключательной функции
- 8. СклеиваниеИз СДНФ можно получить другие импликанты путем
- 9. Простая импликантаПростой импликантой функции f(х) называется любая
- 10. СкДНФВ булевой алгебре переключательных функций утверждается и
- 11. Исключение «лишних» простых импликантИногда из сокращенной ДНФ
- 12. Тупиковые ДНФСокращенная ДНФ переключательной функции называется тупиковой,
- 13. ОТДНФМинимальных ДНФ тоже может быть несколько. Минимальная
- 14. ЧМДНФПоиск минимальной ДНФ всегда связан с перебором
- 15. Минимизация не полностью определенных ПФ При минимизации
- 16. 2.Метод Квайна - Мак -КласкиМетод основан на
- 17. 2.Метод Квайна - Мак -КласкиДля упорядочения целесообразно
- 18. 2.Метод Квайна - Мак -КласкиМак-Класки формализовал метод
- 19. 2.Метод Квайна - Мак -КласкиПусть задана функция Сгруппируем эти конституенты единицы по числу единиц:
- 20. 2.Метод Квайна - Мак -КласкиДальнейшие склеивания невозможны. Нахождение минимальных ДНФ далее производится по импликантной таблице
- 21. Метод Блейка-Порецкого. Метод Блейка-Порецкого.Метод позволяет получать сокращенную
- 22. 3.Минимизация переключательных функций по картам Карно При
- 23. Минимизация переключательных функций по картам КарноМетод минимизации
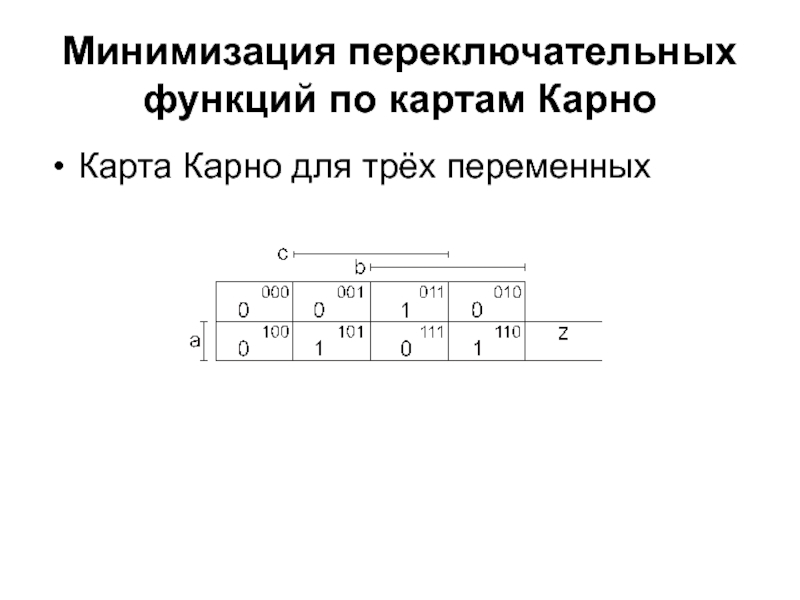
- 24. Минимизация переключательных функций по картам КарноКарта Карно для трёх переменных
- 25. Минимизация переключательных функций по картам КарноКарта Карно для четырёх переменных
- 26. Минимизация переключательных функций по картам КарноМинимизация переключательной
- 27. Минимизация переключательных функций по картам КарноПравильными контурами
- 28. Минимизация переключательных функций по картам Карночетырехклеточный – квадрат из четырех соседних клеток, окруженных нулями;
- 29. Минимизация переключательных функций по картам Карновосьмиклеточный – куб из восьми соседних клеток, окруженных нулями;
- 30. Минимизация переключательных функций по картам КарноПо карте
- 31. Скачать презентанцию
1.Понятие о минимизации ПФПри технической реализации переключательных функций, широко используемых в вычислительной технике, системах автоматического (автоматизированного) управления и контроля, возникает задача нахождения наиболее экономичного представления соответствующих переключательных функций.
Слайды и текст этой презентации
Слайд 21.Понятие о минимизации ПФ
При технической реализации переключательных функций, широко используемых
Слайд 31.Понятие о минимизации ПФ
Ограничимся целью нахождения наиболее простого представления переключательной
функции в смысле наименьшего числа входящих в нее символов (букв).
Процесс получения такого представления будем называть минимизацией.Слайд 41.Понятие о минимизации ПФ
Методы минимизации разрабатываются применительно к каждой отдельной
функциональной полной системе элементных переключательных функций. Наиболее детально такие методы
разработаны для систем из дизъюнкции, конъюнкции и инверсии.Слайд 5Импликанта и имплицента
При минимизации переключательных функций существенную роль играют понятия
импликанты, простой импликанты, имплиценты и простой имплиценты.
Пусть f(x), g(x), p(x)
– полностью определенные функции, причем под х понимается некоторый набор из n переменных (х1х2...хn). Функция f(х) определена на рабочих (единичных) наборах М1[f(х)] и множестве запрещенных (нулевых) наборов М0[f(х)].
Функция g(x) определена на множестве рабочих (единичных) наборов М1[g(x)], а функция р(х) – на множестве запрещенных (нулевых) наборов М0[р(х)].
Слайд 6Импликанта
Переключательная функция g(х) называется импликантой переключательной функции f(х), если множество
рабочих (единичных) наборов функции g(х) совпадает или является подмножеством множества
рабочих наборов функции f(х), т.е. М1[g(x)]⊆ М1[f(x)], где ⊆ – знак включения в множество, означающий, что всякий элемент левого множества является элементом правого множества. При этом говорят, что М1[f(x)] содержит М1[g(x)], т.е. в соответствии с определением импликации g(x)→f(x).Слайд 7Имплицента
Переключательная функция р(х) является имплицентой переключательной функции f(х), если множество
запрещенных (нулевых) наборов функции р(х) совпадает или является подмножеством множества
запрещенных (нулевых) наборов функции f(х), т.е. М0[р(x)]⊆ М0[f(x)].Слайд 8Склеивание
Из СДНФ можно получить другие импликанты путем всевозможных группировок ее
членов (конституент) и многократного использования (по возможности) закона склеивания, пока
не останется конъюнкций, отличающихся значениями одной переменной.Слайд 9Простая импликанта
Простой импликантой функции f(х) называется любая элементарная конъюнкция в
g(х), являющаяся импликантой функции и обладающая тем свойством, что никакая
ее собственная часть уже не является импликантой.Слайд 10СкДНФ
В булевой алгебре переключательных функций утверждается и доказывается: 1) дизъюнкция
любого числа импликант переключательной функции также является импликантой этой функции;
2) любая переключательная функция равносильна дизъюнкции всех своих простых импликант, и такая форма ее представления называется сокращенной ДНФ (СкДНФ).
Слайд 11Исключение «лишних» простых импликант
Иногда из сокращенной ДНФ можно убрать одну
или несколько простых импликант, не нарушая количества необходимых рабочих наборов.
Такие простые импликанты назовем лишними.Исключение лишних простых импликант из сокращенной ДНФ – второй этап минимизации.
Слайд 12Тупиковые ДНФ
Сокращенная ДНФ переключательной функции называется тупиковой, если в ней
отсутствуют лишние простые импликанты.
Устранение лишних простых импликант из сокращенной ДНФ
переключательной функции не является однозначным процессом, т.е. переключательная функция может иметь несколько тупиковых ДНФ.Тупиковые ДНФ, содержащие минимальное число букв, являются минимальными.
Слайд 13ОТДНФ
Минимальных ДНФ тоже может быть несколько. Минимальная ДНФ функции, найденная
путем построения и перебора всех тупиковых ДНФ и выбора из
них самой минимальной, называется общей (абсолютной) тупиковой ДНФ.Слайд 14ЧМДНФ
Поиск минимальной ДНФ всегда связан с перебором решений. Существуют методы
уменьшения перебора, но он всегда имеется. Как правило, ограничиваются нахождением
одной или нескольких тупиковых ДНФ, из которых выбирают минимальную, – её называют частной минимальной ДНФ и считают близкой к общей (абсолютной).Слайд 15Минимизация не полностью определенных ПФ
При минимизации не полностью определенных
переключательных функций особенностью является то, что необходимо найти такое ее
доопределение за счет условных наборов, которое соответствует минимальной ДНФ, содержащей наименьшее число букв.Слайд 162.Метод Квайна - Мак -Класки
Метод основан на попарном сравнении и
склеивании при возможности всех конституент (членов СДНФ). Для этого каждая
конституента сравнивается с последующими, что приводит к получению импликант. Полученные импликанты вновь подвергаются сравнению и при возможности склеиваются – и т.д. до тех пор, пока оставшиеся импликанты уже не будут поддаваться склеиванию. Это и есть простые импликанты, их дизъюнкция представляет собой сокращенную ДНФ.Слайд 172.Метод Квайна - Мак -Класки
Для упорядочения целесообразно разбивать конституенты на
группы по числу неинверсированных переменных.
В этом случае каждая очередная
конституента, начиная сверху, сравнивается только с конституентами группы, соседней снизу, с числом неинверсированных переменных на единицу больше.Слайд 182.Метод Квайна - Мак -Класки
Мак-Класки формализовал метод Квайна, с целью
использования ЭВМ. Формализация заключается в записи конституент единицы (членов СДНФ)
их двоичными номерами. Все номера разбиваются на непересекающиеся группы по числу единиц в двоичном номере. Склеивания производятся только между соседними группами. Ликвидируемый разряд обозначается знаком «–» («тире»). Дальнейшие группы из полученных импликант образуются с учетом однинакового расположения тире. Такое обозначение импликант называется обобщенными кодамиСлайд 192.Метод Квайна - Мак -Класки
Пусть задана функция
Сгруппируем эти конституенты
единицы по числу единиц:
Слайд 202.Метод Квайна - Мак -Класки
Дальнейшие склеивания невозможны. Нахождение минимальных ДНФ
далее производится по импликантной таблице
Слайд 21Метод Блейка-Порецкого.
Метод Блейка-Порецкого.
Метод позволяет получать сокращенную ДНФ булевой функции по
ее произвольной ДНФ, а не по СДНФ, как в методах
Квайна и Квайна-Мак-Класки, используя закон обобщенного склеиванияСлайд 223.Минимизация переключательных функций по картам Карно
При решении задач минимизации
как полностью определенных, так и не полностью определенных переключательных функций,
зависящих от небольшого числа переменных, широкое применение находят графические методы.Слайд 23Минимизация переключательных функций по картам Карно
Метод минимизации по картам Карно
позволяет графически получать экономное покрытие переключательной функции правильными конфигурациями её
единиц.Карта Карно – это таблица истинности специального вида, в которой переменные функции расположены не одномерным, а двумерным массивом (по горизонтали и вертикали), причем каждому набору переменных поставлена в соответствие одна клетка.
Слайд 26Минимизация переключательных функций по картам Карно
Минимизация переключательной функции по карте
Карно в классе ДНФ заключается в покрытии ее единиц минимальным
количеством максимальных правильных контуров. В эти контуры могут включаться и условные наборы. Контуры могут пересекаться, но не могут включаться друг в друга – иначе не получатся простые импликанты.Слайд 27Минимизация переключательных функций по картам Карно
Правильными контурами для карты 4-х
переменных могут быть следующие:
одноклеточный – одна клетка с единицей, окруженная
нулями;двухклеточный – две соседние клетки, окруженные нулями;