Многоэлектронные атомы

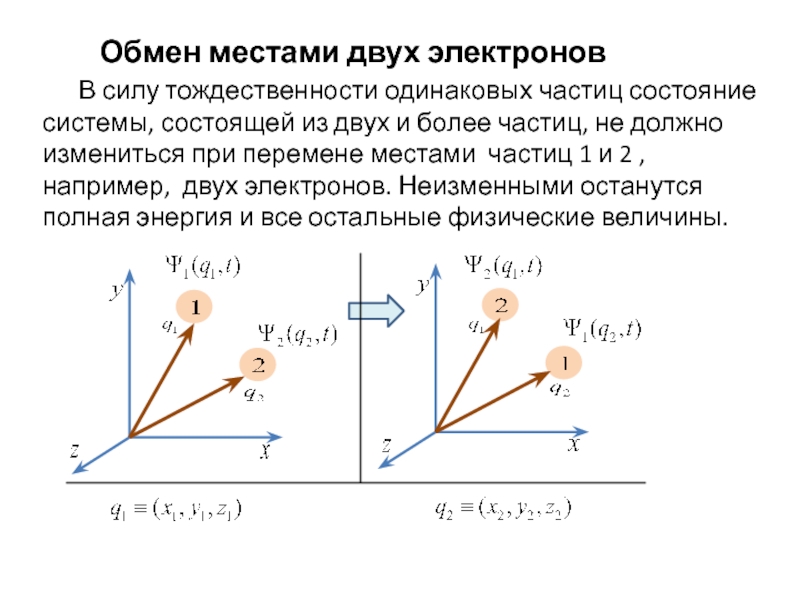
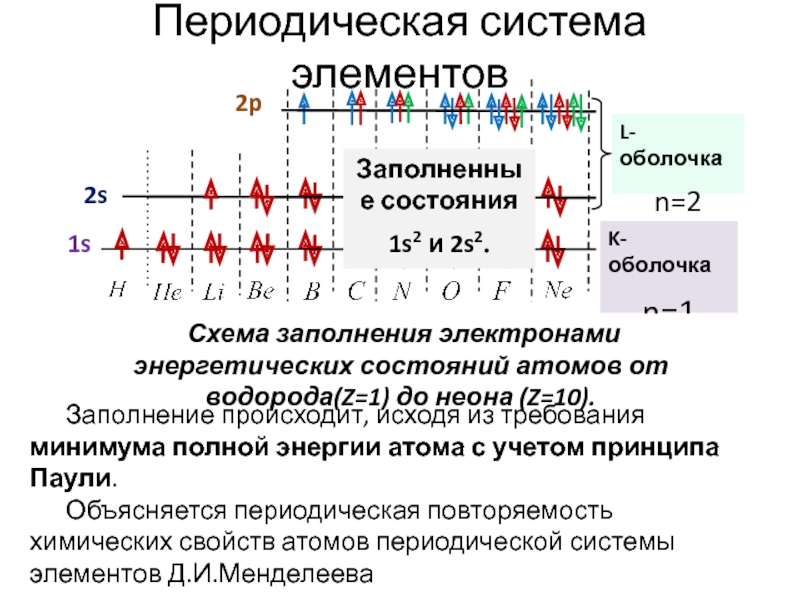
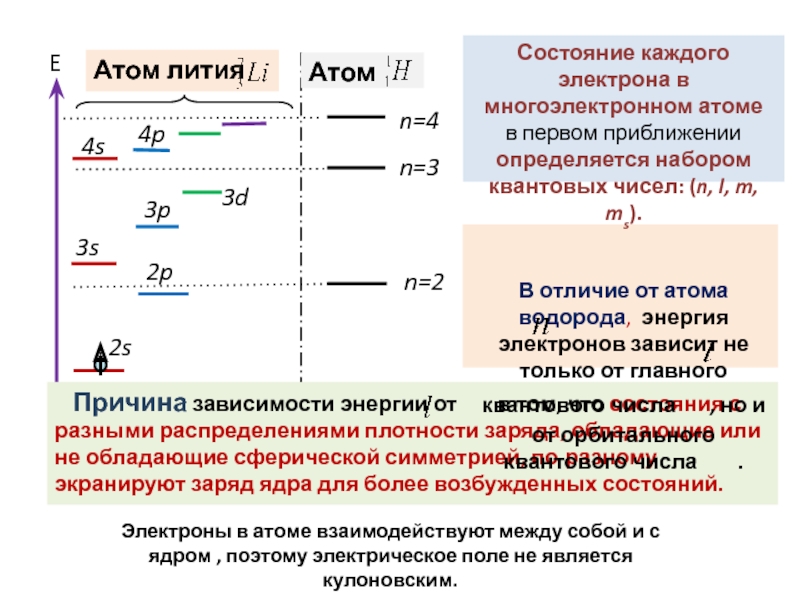
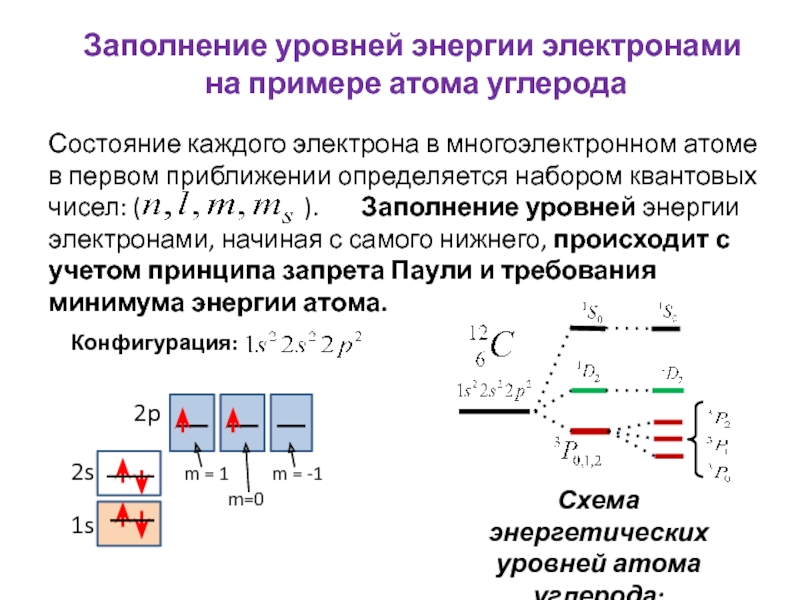
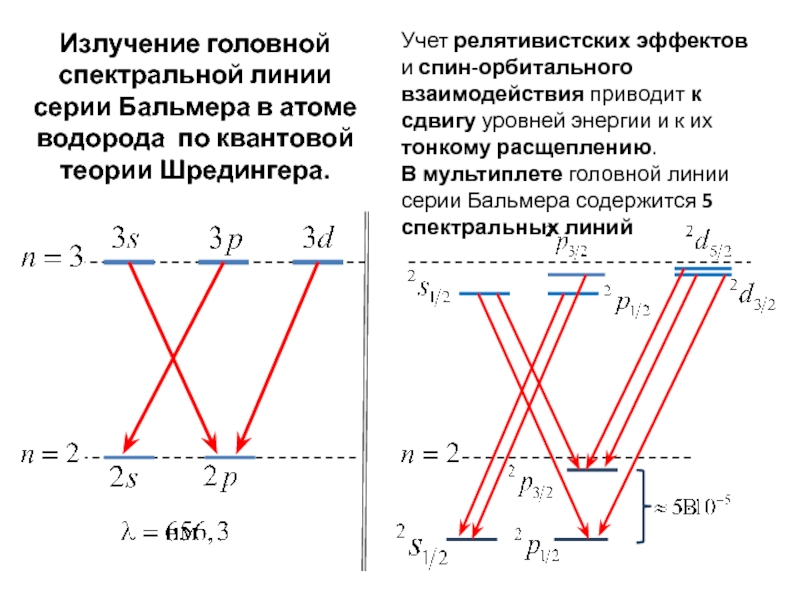
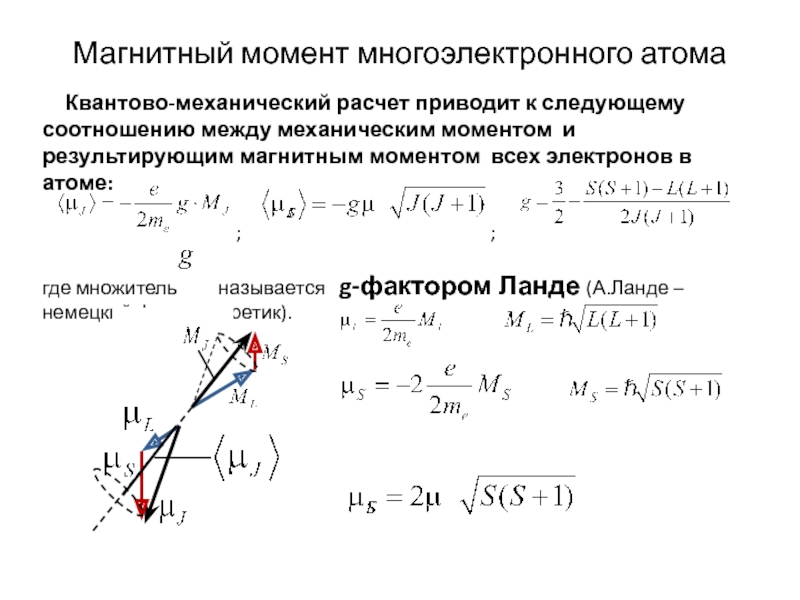
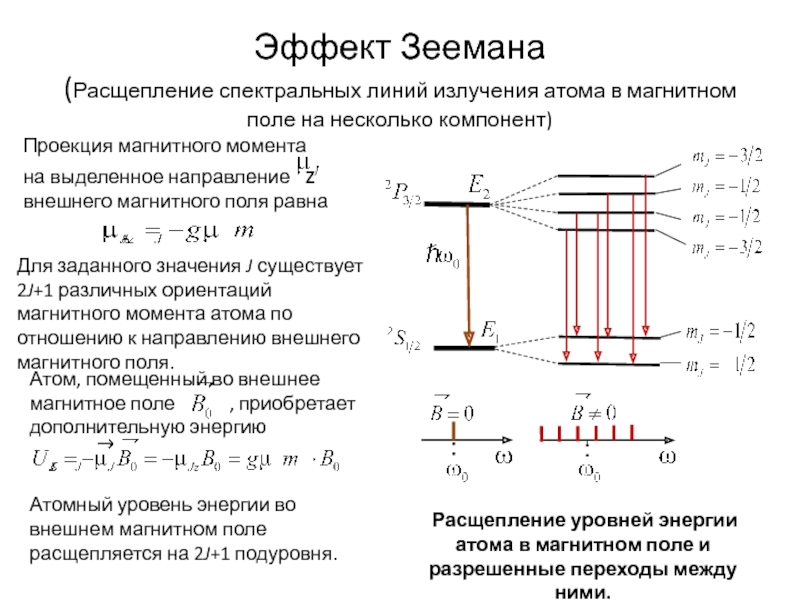
всегда можно, хотя бы в принципе, определить

индивидуальную траекторию каждой из многих
одинаковых частиц.
В квантовой механике
траектория «потеряна» с самого начала согласно соотношениям неопределенностей.
Поэтому одинаковые частицы, которые имеют одинаковые значения массы, электрического заряда, спина и т.д. и находятся в общей области существования, оказываются тождественными и принципиально неразличимыми.

состоящей из двух и более частиц, не должно измениться при

перемене местами частиц 1 и 2 , например, двух электронов. Неизменными останутся полная энергия и все остальные физические величины.

Обмен местами двух электронов

оператор перестановки частиц местами :

(1)

Поскольку обе волновые функции в (1) описывают одно и то же квантовое состояние, то они являются решением уравнения Шредингера


и могут различаться только постоянным множителем. Тогда уравнение (1) можно переписать как
(2)
Подействуем на левую и правую части уравнения (2) оператором перестановки

Так как дважды применяемый оператор перестановки не меняет волновую функцию , то получаем:

все возможные состояния системы из одинаковых частиц

делятся на два типа:

Симметричные состояния,
для которых - функция системы одинаковых частиц не меняет знака при перестановке частиц местами:

- функция меняет знак при перестановке частиц

местами:




Частицы, состояния которых описываются антисимметричными - функциями, называются фермионами, они подчиняются статистике Ферми-Дирака, развитой итальянским физиком Э.Ферми и английским физиком П.Дираком.

взаимодействием между частицами можно пренебречь, то состояние отдельной частицы в

системе описывается волновой функцией и набором квантовых чисел, а состояние всей системы – произведением волновых функций отдельных частиц.
Предположим, что в системе ферми-частиц, где возможен обмен местами, две частицы находятся в одном и том же стационарном состоянии , то есть . Тогда волновая функция , а это означает, что такое состояние физически не может быть реализовано.
Принцип запрета В.Паули (1925 г. , немецкий физик):
В системе тождественных фермионов не может быть двух частиц, находящихся в одном и том же квантовом состоянии с одним и тем же набором кантовых чисел
.
 

водорода(Z=1) до неона (Z=10).


Заполненные состояния
1s2 и 2s2.
Заполнение

происходит, исходя из требования минимума полной энергии атома с учетом принципа Паули.
Объясняется периодическая повторяемость химических свойств атомов периодической системы элементов Д.И.Менделеева

поэтому электрическое поле не является кулоновским.

1. В результате наиболее сильного взаимодействия орбитальных магнитных моментов отдельных

электронов образуются суммарный магнитный орбитальный момент и механический момент
всех электронов в атоме ,
где - орбитальное квантовое число атома (целое число либо ноль).
2. В результате менее сильного взаимодействия спиновых магнитных моментов отдельных электронов образуется суммарный магнитный спиновый момент и суммарный спин
всех электронов в атоме,

где - квантовое число суммарного спина. Если в атоме четное число электронов, то квантовое число является целым числом, либо равно нулю. При нечетном числе электронов квантовое число принимает полуцелые значения.
3. Наиболее слабое спин-орбитальное взаимодействие между магнитными моментами и приводит к образованию результирующего магнитного момента и механического момента всего атома

Квантовое число принимает значения:
для заданной пары значений и .




 

понимается одна из следующих букв

(S,P, …) в схеме обозначений:
 

Квантовая теория, исходя из закона сохранения моментов импульса,

обосновывает правила отбора для разрешенных оптических переходов атома из одного квантового состояния в другое.

Примеры.
Разрешенные переходы:

Запрещенные
переходы:

квантовой теории Шредингера.
Учет релятивистских эффектов и спин-орбитального взаимодействия приводит

к сдвигу уровней энергии и к их тонкому расщеплению.
В мультиплете головной линии серии Бальмера содержится 5 спектральных линий

следующему соотношению между механическим моментом и результирующим магнитным моментом всех

электронов в атоме:
   
; ;
где множитель называется g-фактором Ланде (А.Ланде – немецкий физик-теоретик).

несколько компонент)
Расщепление уровней энергии атома в магнитном поле и

разрешенные переходы между ними.

Проекция магнитного момента на выделенное направление z внешнего магнитного поля равна

Для заданного значения J существует 2J+1 различных ориентаций магнитного момента атома по отношению к направлению внешнего магнитного поля.

Атом, помещенный во внешнее магнитное поле , приобретает дополнительную энергию

Атомный уровень энергии во внешнем магнитном поле расщепляется на 2J+1 подуровня.