Слайд 2 Пусть имеется пространство элементарных событий
U, на нем построено поле событий и для каждого события
А из этого поля определена вероятность Р(А).
Каждому элементарному событию gi из U сопоставим несколько чисел: ξ i1 , ξ i2 , ξ i3 , ... ξ ik или вектор ξi. Потребуем, чтобы для любых хj ( -∞ < хj <+∞ ) , j = 1, 2 ... k , множество А тех g , для которых ξ j < хj ( j = 1, 2, ... k) , принадлежало полю событий, т.е. для него определена вероятность Р{ ξ 1 < x1 , ξ 2 < x2 , ... ξ k < xk } = P(A) = F( x1, x2, ... xk ). Тогда ξ называется многомерной случайной величиной, или случайным вектором, а F( x1, x2, ... xk ) ее функцией распределения.
Слайд 3Примеры:
1 . Координаты молекулы, находящейся в сосуде с
газом, (x,y,z) или компоненты ее скорости (Vx,Vy,Vz) - можно рассматривать как
трехмерные случайные величины
Слайд 4 2 . В задаче "о встрече" время прихода одного
участника (х1) и другого (х2), если условия их прихода известны
(скажем - любой момент в течение заданного часа), пару чисел х1, х2 можно рассматривать как двумерную случайную величину
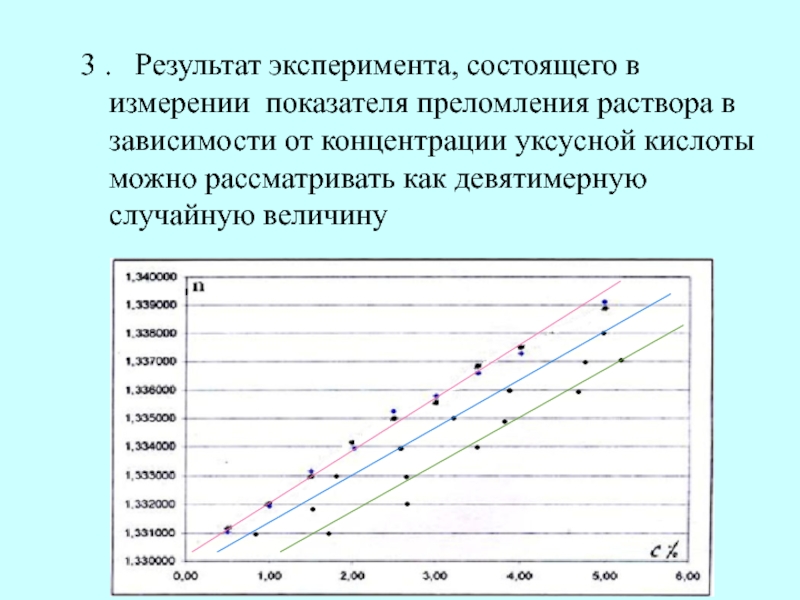
Слайд 5 3 . Результат эксперимента, состоящего в измерении показателя преломления
раствора в зависимости от концентрации уксусной кислоты можно рассматривать как
девятимерную случайную величину
Слайд 6Свойства многомерной функции распределения:
1 . F( x1, x2, ... xk-1,- ∞) = 0, т.е. если
хоть один из аргументов принимает значение -∞, то F=0.
2
. F( x1, x2, ... xk ) не убывающая функция любого аргумента
3. F( x1, x2, ... xk-1, ∞) = F( x1, x2, ... xk-1 ), т.е. если один из аргументов принимает значение ∞, то размерность случайной величины уменьшается на 1.
Слайд 7 Многомерные случайные величины могут быть непрерывными,
т.е. принимать любые значения в некоторой области к-мерного пространства (например,
упомянутые выше компоненты скорости молекулы).
У них F( x1, x2, ... xk ) непрерывная функция всех аргументов. Для них определена
к-мерная плотность распределения
p( x1, x2, ... xk ), которая есть производная от функци распределения.
Слайд 8 Вероятность того, что случайный вектор примет
значение, лежащее в области V к-мерного пространства, равна интегралу по
этой области от к-мерной плотности распределения.
Интеграл по всем переменным от - ∞ до + ∞ от к-мерной плотности распределения равен 1.
Интеграл по одной переменной от - ∞ до + ∞ от к-мерной плотности распределения равен плотности распределения (к-1)-мерной случайной величины.
Например:
Слайд 9 Многомерные случайные величины могут быть
дискретными, т.е. каждая компонента случайного вектора может принимать только конечное
или счетное множество определенных значений.
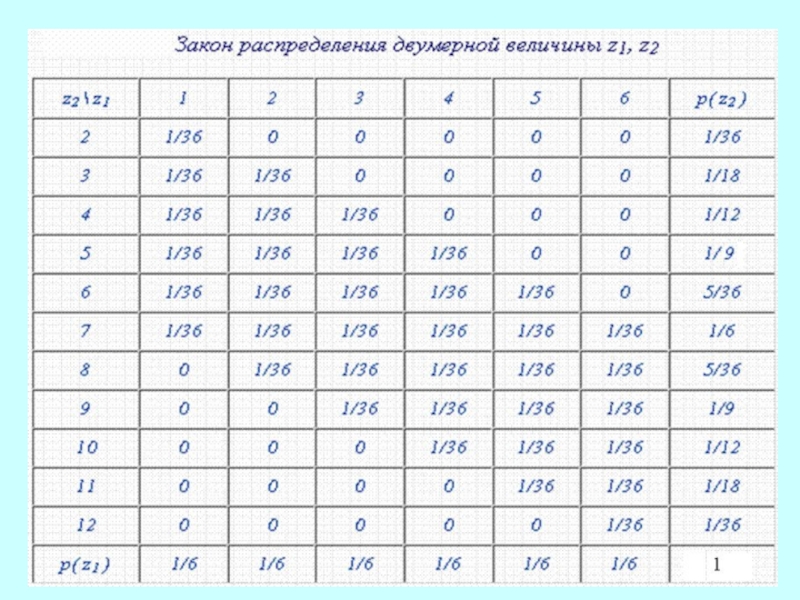
Например, рассмотрим эксперимент по бросанию одновременно двух костей, с каждым элементарным событием свяжем два числа ( z1, z2 ), где z1 - число очков на первой кости, z2 - сумма очков на двух костях. Тогда ( z1, z2 ) - двумерная случайная величина, поскольку известна вероятность р( хi, хk ) пересечения событий, состоящих в том, что z1 примет значение хi, а z2 - хk . Для дискретных случайных величин закон распределения задается вероятностями всевозможных комбинаций их значений. Для двумерной величины при небольшом числе возможных значений это удобно представить в виде таблицы, где на пересечении столбца z1 и строки z2 стоит вероятность р( z1, z2 )
Слайд 11 Просуммировав все значения р( z1, z2 ) вдоль каждой
строки, мы получим вероятности определенных значений z2 , т.е. закон распределения
одномерной величины z2 . Аналогично, сумма по столбцам даст закон распределения одномерной величины z1 . Сумма всех чисел в таблице должна быть равна 1 .
Математическим ожиданием многомерной случайной величины называется вектор, компоненты которого являются математическим ожиданием каждой отдельной компоненты случайного вектора.
M( z1, z2, ... zk ) = ( Mz1, Mz2, ... Mzk ).
Mzi вычисляются как сумма или интеграл так же, как и для одномерных случайных величин .
Слайд 12 Дисперсия многомерной случайной величины описывается
ковариационной матрицей .
Это таблица чисел размерности К×К для
К-мерной величины, у которой на диагонали стоят дисперсии соответствующих одномерных величин, вычисляемых обычным образом, а ij-тым элементом является bij - коэффициент ковариации i-той и j-той компоненты случайного вектора.
Слайд 13 Коэффициент ковариации случайных величин zi , zj ,
обозначаемый иногда как cov(zi,zj), есть математическое ожидание произведения отклонений каждой
из этих величин от своего математического ожидания:
Для вычисления коэффициента ковариации надо знать закон распределения двумерной случайной величины (zi,zj). Тогда для непрерывных величин:
Слайд 14для дискретных величин:
Здесь суммирование ведется по всем t значениям, которые
принимает величина zi и всем q значениям, которые принимает величина
zj .
Преобразовав , получим более удобную формулу для вычисления коэффициента ковариации
Слайд 15 Часто используется понятие: коэффициент корреляции rij -
это коэффициент ковариации, деленный на корень из произведения дисперсий
i-той и j-той компонент случайного вектора
доказательство:
|rij|<=1
Слайд 16
Компоненты многомерной случайной величины называются независимыми, если многомерная функция
распределения, многомерная плотность распределения, вероятность определенного набора значений распадаются на
произведение соответствующих одномерных функций или вероятностей
Случайные величины независимы, если независимы
события А: ξi Для независимых событий Р(АВ)=Р(А)*Р(В), т.е.
F(xi,xk)=F(xi)*F(xk). Соответственно:
p(xi,yj,zk)=p(xi)p(yj)p(zk)
Слайд 17Математическое ожидание суммы случайных величин равно сумме их матожиданий
всегда
Математическое ожидание произведения независимых случайных величин равно произведению их матожиданий
Дисперсия
суммы независимых случайных величин равна сумме их дисперсий.
Коэффициенты ковариации и корреляции независимых случайных величин равны 0, следовательно, ковариационная матрица - диагональна
Слайд 18Если r=0, то не обязательно случайные величины независимы.
Пусть есть 2
генератора, вырабатывающие числа z1. z2, равные 0 или 1 с
вероятностями 1/2. Рассмотрим закон распределения двумерной величины х1, х2 , построенной по правилу: х1= z1+ z2, х2= z1- z2.
Mx1=1; Mx2=0
M(x1x2)=
-1/4+1/4=0
Cov(x1x2)=0
r12=0
Они не независимы: p(1,1)=1/4; p(1)p(1)=1/8
0
1/4
0
1/4
1/4
1/4
1/4
1/4
1/4
1/4
1/2
1/2
0
0
0
1
Слайд 19Эллипсоид рассеяния- это область, в которой
значения многомерной случайной величины
лежат с наибольшей вероятностью.
Пример: х, у независимы. Мх=а, My=b
C=1
В данном случае это эллипс
с центром в точке а, b
и осями
Слайд 21Сущность закона больших чисел состоит в том , что при
большом числе независимых опытов частота появления какого-то события близка к
его вероятности.
Этот известный факт следует из теоремы Чебышева.
Сначала докажем неравенство
Обозначим:
Слайд 22Среднее арифметическое сходится к матожиданию
по вероятности
Сходимость по вероятности отличается
от обычной сходимости тем, что нельзя указать такого n, при
котором разность станет наверняка меньше ε , хотя и ничтожно малая, но существует вероятность и большего отклонения.
При независимых испытаниях
при n→∞
При большом числе испытаний частота появления события мало отличается от его вероятности
Слайд 23ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА И ЕЕ СЛЕДСТВИЯ
Слайд 24Характеристические функции случайных
величин.
Определение:
Если х и у независимы, то
Если x=σz+a,
то
Слайд 25 Характеристическая функция
нормально распределенной величины
используем
обозначение
х~N(a,σ2)
Положим:
=
z~N(0,1)
Слайд 26 Нормальное распределение -наиболее распростра-ненное в природе
распределение случайных величин. Математическим обоснованием этого факта служит центральная предельная
теорема:
Сумма большого числа как угодно распределенных независимых случайных величин распределена асимптотически нормально, если только слагаемые вносят равномерно малый вклад в сумму.
Это значит, что чем больше независимых слагаемых в сумме, тем ближе закон ее распределения к нормальному. Вместо суммы часто рассматривают среднее арифметическое большого числа случайных величин, оно отличается от суммы только множителем (1/n) , поэтому его распределение также стремится к нормальному с ростом числа n суммируемых величин. Поскольку случайные величины, с которыми мы сталкиваемся, например, при измерениях, есть результат действия множества независимых факторов, понятно, почему измеряемые значения, как правило, распределены нормально.
Слайд 27Докажем для случая одинаково распределенных
величин xk.
Mxк =a; Dxk =σ2
Образуем
Mwк=0. Dwк=1
Построим
характеристическую функцию
Слайд 28Применим к распределению Бернулли.
xk=ξk Mξ=p
Dξ=pq
теорема Муавра-Лапласа
Поскольку плотность нормального
распределения с матожиданием 0 и дисперсией 1, а также значение интеграла от этой плотности в пределах от 0 до z как функция z табулированы , то легко найти вероятность попадания х, а значит и m, при известных n, p в любой интервал.
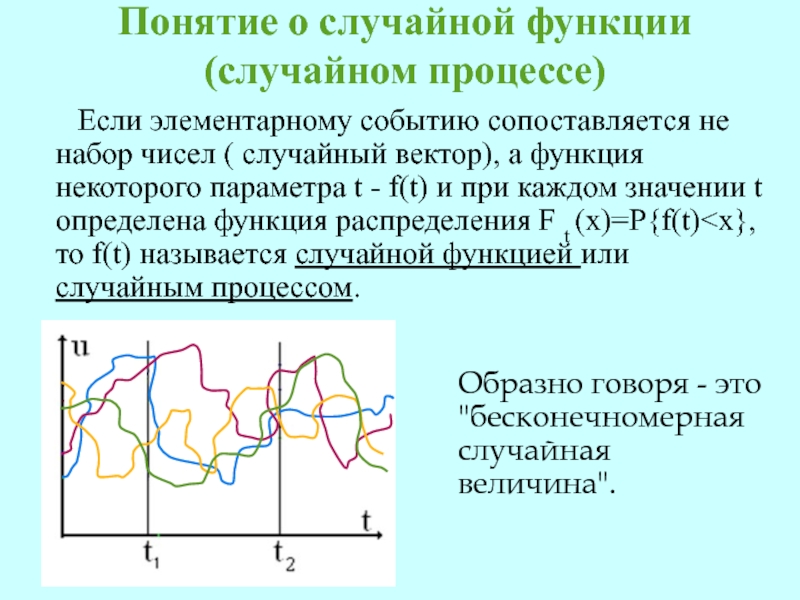
Слайд 29Понятие о случайной функции (случайном процессе)
Если
элементарному событию сопоставляется не набор чисел ( случайный вектор), а
функция некоторого параметра t - f(t) и при каждом значении t определена функция распределения F t (x)=P{f(t)
Образно говоря - это "бесконечномерная случайная величина".
Слайд 30 Если F t (x) не зависит от t
, процесс называется стационарным. Числовые характеристики случайного процесса ( математическое
ожидание и дисперсия ) при фиксированном t определяются так же, как и для обычной случайной величины , если известны плотность распределения рt(х) или рt(xi) (если f принимает дискретный ряд значений). Для стационарного процесса эти характеристики от t не зависят.
Характеристики стационарного процесса можно определить усреднением по параметру
Если результаты вычисления числовых характеристик стационарного процесса путем усреднения по параметру и по ансамблю реализаций дают одинаковый результат, процесс называется эргодическим.
Слайд 31Аналогом ковариационной матрицы , которая характеризует связь между компонентами случайного
вектора, для случайного процесса служит автокорреляционная функция Г(τ), показывающая как
быстро с изменением параметра могут меняться значения случайной функции.
Г(0)=Df
Связь спектра и автокорреляционной функции
Спектр- это Фурье образ f(t)
Положим, что процесс стационарный и Mf=0
Спектр мощности сигнала f(t), т. е. квадрат модуля Фурье-образа f(t), S(ω)=V(ω)*V(ω) пропорционален Фурье-образу функции корреляции Г(τ).
Слайд 32Добавив в показатель экспоненты ± iωt и перейдя к
переменным
t и
Отсюда
Df= Г(0)~S(ω)Δω
Слайд 33Марковский процесс
Если процесс состоит из дискретного ряда значений хк
и вероятность перехода в следующий момент времени из состояния
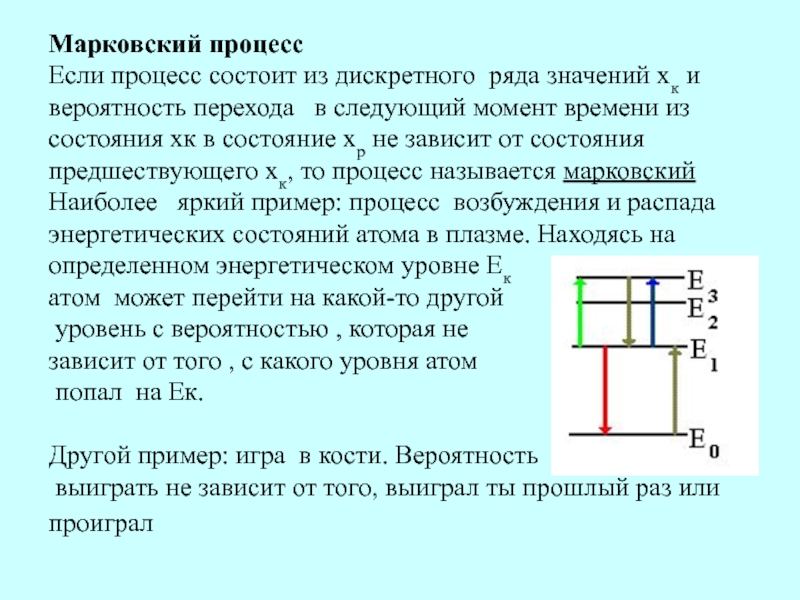
хк в состояние хр не зависит от состояния предшествующего хк, то процесс называется марковский Наиболее яркий пример: процесс возбуждения и распада энергетических состояний атома в плазме. Находясь на определенном энергетическом уровне Ек
атом может перейти на какой-то другой
уровень с вероятностью , которая не
зависит от того , с какого уровня атом
попал на Ек.
Другой пример: игра в кости. Вероятность
выиграть не зависит от того, выиграл ты прошлый раз или проиграл
Слайд 34На этом раздел
«Теория
вероятностей»
закончен.