Множественная регрессия

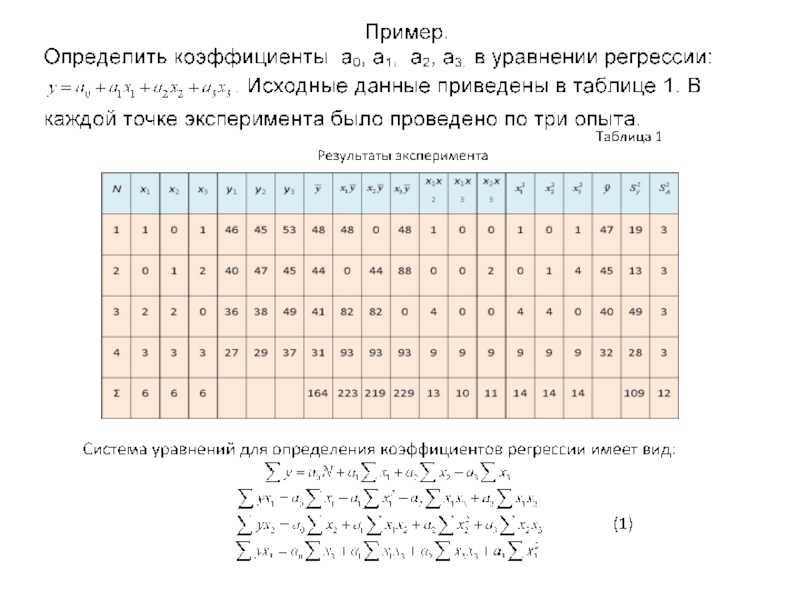
выходного показателя с несколькими переменными, необходимо применить методы множественной регрессии.

В общем случае условию равенства (1) всегда соответствует относительно большая система уравнений. Например, для отыскания коэффициентов уравнения вида

необходимо решить систему уравнений:








Подобным образом можно получить систему уравнений для уравнения с любым числом членов, но при добавлении каждого нового члена трудоемкость решения резко возрастает. Точность модели оценивается по остаточной дисперсии:



где — число коэффициентов уравнения.

(1)

(2)

(3)

случайные величины нормально распределены;
— дисперсия зависимой переменной одинакова при всех

значениях аргумента;
— отдельные наблюдения переменных не связаны друг с другом, т. е. являются независимыми.
Практически первые два условия невыполнимы. Поэтому возникает вопрос, можно ли пользоваться изложенными методами при каких-либо отклонениях указанных условий от требуемых? В настоящее время считается, что методами корреляционного и регрессионного анализов можно пользоваться и тогда, когда зависимая переменная не распределена нормально, а наблюдения зависимы, лишь бы распределения были одновершинными и в некоторой степени симметричными.
Коэффициенты уравнений теоретической линии регрессии в общем случае оцениваются с ошибкой


где — общее обозначение члена функции .
Следует помнить, что при небольшом числе степеней свободы становится ненадежной оценкой. В этом случае следует пользоваться ошибкой воспроизводимости .Тогда оценкой среднего квадратического отклонения кривой регрессии будет величина


Доверительные интервалы для теоретической линии регрессии

(4)

(5)

(6)

составленную из найденных коэффициентов парной корреляции.
Пусть необходимо получить связь
Система нормальных

уравнений для нее

Представим связь ( 7) в стандартизованной форме

и запишем систему уравнений для нее, разделив все члены на

(7)

(8)

(9)

(10)

(11)

множественной корреляции
Коэффициент множественной корреляции не может быть по абсолютной

величине больше единицы.

В первом уравнении системы (7) все суммы обращаются в ноль, откуда

(12)

(13)