Модуль действительного числа

Содержание

1. Модуль действительного числа
2. Цели и задачи урокаВвести определение модуля действительного
3. Определение. Например: |8|=8; |-8|=-(-8)=8;
4. Свойства модуля
5. Геометрический смысл модуля Числовая прямая служит хорошим
6. Пример. Решите уравнение: а) |x-3|=6 б) |x+5|=3 в)
7. Слайд 7
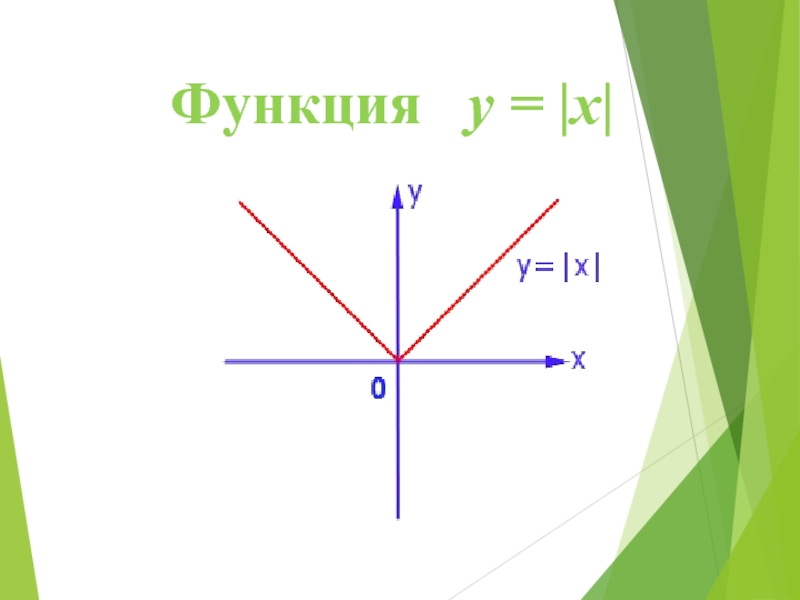
8. Функция y = |x|
9. Слайд 9
10. Решить уравнение |x-1| = 4 1 способ (аналитический)Задание 2
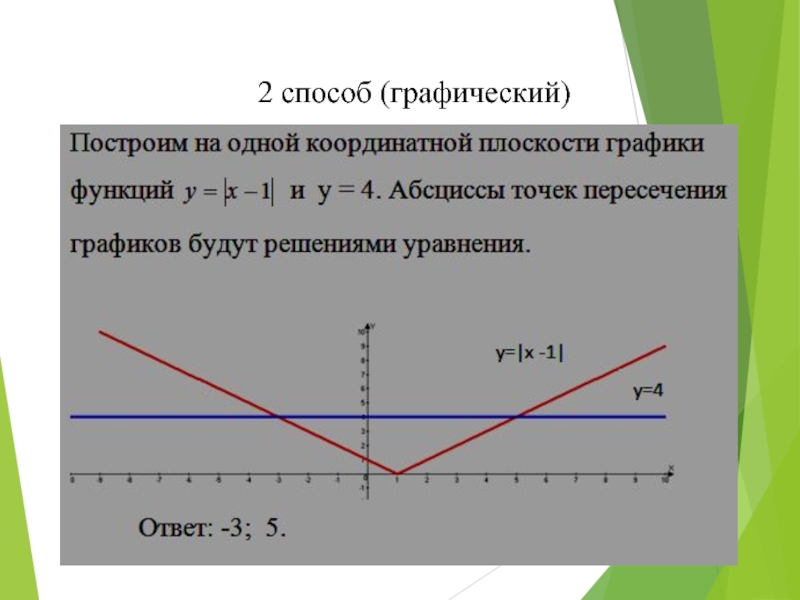
11. 2 способ (графический)
12. 3 способ
13. Модуль действительного числа. Тождество Рассмотрим выражение , если а>0,
14. Модуль действительного числа. Пример. Упростить выражение если: а) а-2≥0 б) a-2
15. Модуль действительного числа. Пример. Вычислить Решение. Мы знаем что: Осталось раскрыть модули Рассмотрим первое выражение:
16. Рассмотрим второе выражение: Используя определение раскроем знаки модулей: В итоге получили: Ответ: 1.
17. Закрепление нового материала. № 16.2, №16.3, №16.4, №16.12, №16.16 ( а, г), №16.19
18. Задачи для самостоятельного решения. 1. Решите уравнение: а) |x-10|=3
19. Список использованной литературы:Звавич Л.И. Алгебра. Углубленное изучение.
20. Скачать презентанцию

Цели и задачи урокаВвести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля; Ввести функцию y = |x|, показать правила построения ее графика;Научить разными способами решать уравнения, содержащие модуль;Развивать

Главная
Разное
Модуль действительного числа

Слайды и текст этой презентации

Слайд 1Модуль действительного числа
Автор материала:
Дудниченко Татьяна Анатольевна, учитель математики  первой

квалификационной категории ГАОУ СОШ МГПУ, г. Москва

Модуль действительного числаАвтор материала: Дудниченко Татьяна Анатольевна, учитель математики  первой квалификационной категории ГАОУ СОШ МГПУ, г. Москва

Слайд 2Цели и задачи урока
Ввести определение модуля действительного числа, рассмотреть свойства

и разъяснить геометрический смысл модуля;
Ввести функцию y = |x|,

показать правила построения ее графика;
Научить разными способами решать уравнения, содержащие модуль;
Развивать интерес к математике, самостоятельность, логическое мышление, математическую речь, прививать аккуратность и трудолюбие.

Цели и задачи урокаВвести определение модуля действительного числа, рассмотреть свойства и разъяснить геометрический смысл модуля; Ввести функцию

Слайд 3Определение.
Например:
|8|=8; |-8|=-(-8)=8;

Слайд 4Свойства модуля

Слайд 5Геометрический смысл модуля
Числовая прямая служит хорошим примером множества действительных чисел.

Давайте отметим на числовой прямой две точки a и b

и постараемся найти расстояние ρ(a;b) между этими точками. Очевидно что это расстояние равно b-a, если b>a

Если поменять местами, то есть a>b, расстояние будет равно a-b.

Если a=b то расстояние равно нулю, так как получается точка.
Все три случая мы можем описать единообразно:

Геометрический смысл модуля Числовая прямая служит хорошим примером множества действительных чисел. Давайте отметим на числовой прямой две

Слайд 6 Пример. Решите уравнение:
а) |x-3|=6 б) |x+5|=3 в) |x|=2.8 г)
Решение.
а) Нам

нужно найти на координатной прямой такие точки, которые удалены

от точки 3 на расстояние равное 6.
Такие точки 9 и -3. (Прибавили и отняли шестерку от тройки.)
Ответ: х=9 и х=-3
б) |x+5|=3, перепишем уравнение в виде |x-(-5)|=3.
Найдем расстояние от точки -5 удаленное на 3. Такое расстояние, получается, от двух точек: х=2 и х=-8
Ответ: х=2 и х=-8.
в) |x|=2.8, можно представить в виде |х-0|=2.8 или
Очевидно, что х=-2.8 или х=2.8
Ответ: х=-2.8 и х=2.8.
г) эквивалентно
Очевидно, что

Пример. Решите уравнение: а) |x-3|=6 б) |x+5|=3 в) |x|=2.8 г) Решение. а) Нам нужно найти на координатной прямой такие точки,

Слайд 7

Слайд 8Функция y = |x|

Слайд 9

Слайд 10Решить уравнение |x-1| = 4
1 способ (аналитический)
Задание 2

Слайд 112 способ (графический)

Слайд 123 способ

Слайд 13Модуль действительного числа.
Тождество
Рассмотрим выражение , если а>0, то мы знаем

что .
Но как быть, в случае если a

Ведь не может быть , в
таком случае корень равен отрицательному числу.
Давайте рассмотрим –а.
1. Если а<0 то –а>0.
2.

Давайте обобщим:

По определению модуля:

То есть

Модуль действительного числа. Тождество Рассмотрим выражение , если а>0, то мы знаем что . Но как быть, в

Слайд 14Модуль действительного числа.
Пример. Упростить выражение если:
а) а-2≥0 б) a-2

а) Если а-2≥0, то |a-2|=a-2. Таким образом получаем

б) Если а-2

то |a-2|=-(a-2)=2-a. Таким образом получаем

Слайд 15Модуль действительного числа.
Пример. Вычислить

Решение. Мы знаем что:

Осталось раскрыть модули
Рассмотрим первое

выражение:

Слайд 16 Рассмотрим второе выражение:

Используя определение раскроем знаки модулей:

В итоге получили:

Ответ:

Рассмотрим второе выражение: Используя определение раскроем знаки модулей: В итоге получили: Ответ: 1.

Слайд 17Закрепление нового материала.
№ 16.2, №16.3, №16.4, №16.12, №16.16 ( а,

г), №16.19

Слайд 18 Задачи для самостоятельного решения.
1. Решите уравнение:
а) |x-10|=3 б) |x+2|=1 в)

|x|=2.8 г)

2. Решить уравнение:
а) |3x-9|=33 б)|8-4x|=16 в)|x+7|=-3

3. Упростить выражение
если

а) а-3≥0 б) a-3<0

4. Вычислите

Задачи для самостоятельного решения

Домашнее задание: прочитать материал §16, №16.6 16.11, 16.22

Слайд 19Список использованной литературы:
Звавич Л.И. Алгебра. Углубленное изучение. 8 кл.: задачник

/ Л.И. Звавич, А.Р. Рязановский. – 4-е изд., испр. –

М.: Мнемозина, 2006. – 284 с.
Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений /А.Г. Мордкович. – 12-е изд., стер. – М.: Мнемозина, 2014. – 215 с.
Мордкович А.Г и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 12-е изд., испр. и доп. – М.: Мнемозина, 2014. – 271 с.

Список использованной литературы:Звавич Л.И. Алгебра. Углубленное изучение. 8 кл.: задачник / Л.И. Звавич, А.Р. Рязановский. – 4-е

Скачать презентацию

Теги

Разделы презентаций