Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мокляк Денис Сергеевич преподаватель кафедры техники и технологии
Содержание
- 1. Мокляк Денис Сергеевич преподаватель кафедры техники и технологии
- 2. ОСНОВНЫЕ РАЗДЕЛЫ ОБЩЕЙ ФИЗИКИмеханика термодинамика и молекулярная физикаэлектричество и магнетизмоптикаатомная физикаквантовая физикаядерная физика
- 3. МЕХАНИКА раздел физики, изучающий простейшую форму движения
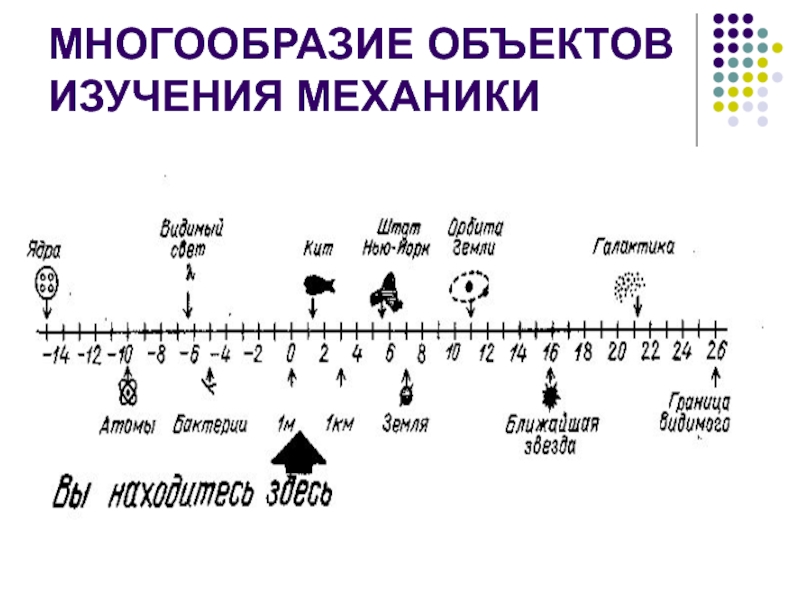
- 4. МНОГООБРАЗИЕ ОБЪЕКТОВ ИЗУЧЕНИЯ МЕХАНИКИ
- 5. ОпределениеМеханика – раздел физики, в котором изучается
- 6. Механика Галилея — Ньютона называется классической механикой.
- 7. Механика делится на три раздела:1) кинематику; 2)
- 8. МеханикаЭлементы кинематики
- 9. Кинематика поступательного движенияМатериальная точка – тело, размеры
- 10. Кинематика поступательного движенияЛюбое движение твердого тела можно
- 11. Кинематика поступательного движенияx=x(t), y=y(t),z=z(t) r = r(t)Кинематические уравнениядвижения материальной точки
- 12. СкоростьДля характеристики движения материальной точки вводится векторная
- 13. СкоростьПри неограниченном уменьшении t средняя скорость
- 14. ПримерПоловину времени тело двигалось
- 15. Ускорение и его составляющиеНЕРАВНОМЕРНОЕ ДВИЖЕНИЕ=Среднее ускорение неравномерного
- 16. ПримерРадиус-вектор материальной точки изменяется со временем по
- 17. РешениеПо определению скорость равна первой производной радиус-вектора по времени:
- 18. РешениеСоставляющие скорости: , следовательно, модуль скорости равен
- 19. Тангенциальная составляющаяускоренияУскорение и его составляющиеНормальная составляющая ускоренияМодуль полного ускорения тела
- 20. Ускорение и его составляющиеВ зависимости от тангенциальной
- 21. ХАРАКТЕРИСТИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯПрямолинейное равномерноеПрямолинейное равноускоренноеПрямолинейное равнозамедленноеРавномерное движение по окружности
- 22. ПРИМЕР. Движение тела, брошенного под углом к горизонту
- 23. ПРИНЦИПЫ КИНЕМАТИКИ ТВЕРДОГО ТЕЛАПоступательное движение твердого тела
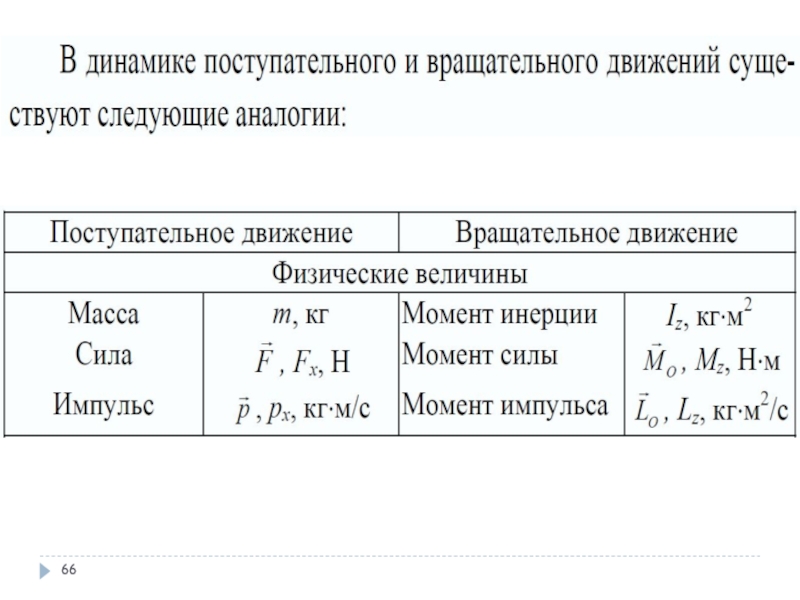
- 24. Переход к вращательному движениюпутьскоростьускорениеРавномерное движение Равноускоренное движение2 закон НьютонамассаУгол поворотасилаМомент силУгловое ускорениеУгловая скоростьМомент инерцииКинематическая энергия
- 25. Угловой скоростью называется векторная величина, определяемая первой
- 26. Связь линейной скорости точки с угловой скоростьюЕсли
- 27. Угловая скорость и угловое ускорениеЧисло полных оборотов,
- 28. Угловая скорость и угловое ускорение
- 29. ПримерПренебрегая сопротивлением воздуха, определить угол, под которым
- 30. РешениеДано: h = 1/4s. Найти: α.Составляющие начальной скорости тела v0x = v0cosα, v0y = v0sinα;Ответ: α=450.
- 31. ПримерДиск радиусом R = 10 см вращается
- 32. ПримерТело вращается вокруг неподвижной оси по закону,
- 33. РешениеДано: φ = 10 + 20t - 2t2; R=0,1 м; t=4 с. Найти: a.Ответ: а = 1,65 м/с2.
- 34. ПримерЗакон движения материальной точки имеет видОпределите модуль
- 35. Еще раз дифференцируем: Решения для модуля скорости
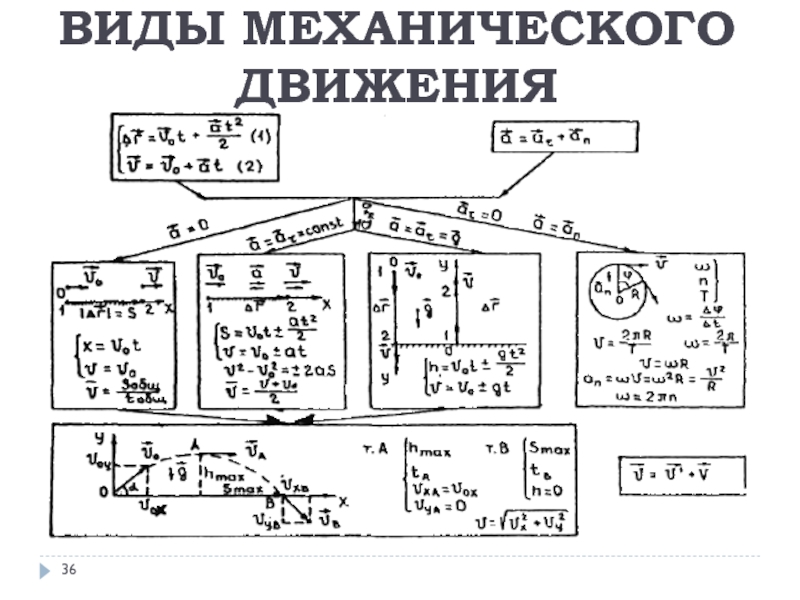
- 36. ВИДЫ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ
- 37. МеханикаДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
- 38. Основные понятияСила — это векторная величина, являющаяся
- 39. Типы взаимодействияРазличные взаимодействия, известные в современной физике,сводятся
- 40. Силы в механикеВ задачах механики учитываются гравитационные
- 41. Силы в механикеГравитационная постоянная G – фундаментальная константа, коэффициент пропорциональности в законе всемирного тяготения
- 42. Силы в механикеС каждым телом неразрывно связано
- 43. Слайд 43
- 44. Силы в механике
- 45. Силы в механике
- 46. Сила тренияРазличают внешнее (сухое) и внутреннее (жидкое
- 47. Сила тренияРазличают внешнее (сухое) и внутреннее (жидкое
- 48. Законы НьютонаПервый закон Ньютона: всякая материальная точка
- 49. ПримерКакого веса балласт Fx надо сбросить с равномерно спускающегося
- 50. РешениеТак как движение равномерное, то по первому
- 51. Второй закон Ньютона: ускорение, приобретаемое материальной точкой
- 52. Законы НьютонаТретий закон Ньютона: всякое действие материальных
- 53. Закон сохранения импульсаСилы взаимодействия между материальными точками
- 54. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕИмпульс мат. точки –
- 55. МеханикаРабота и энергия
- 56. Энергия, работа, мощностьИзменение механического движения тела вызывается
- 57. Чтобы охарактеризовать скорость совершения работы, вводят понятие
- 58. Потенциальные силы в механикеПотенциальными (консервативными) называются силы,
- 59. Потенциальная энергия —механическая энергия системы тел, определяемая
- 60. Кинетическая и потенциальная энергииКинетическая энергия механической системы — энергия механического движения этой системы.
- 61. Полная механическая энергия системы
- 62. Закон сохранения механической энергииЗакон сохранения механической энергии:
- 63. Закон сохранения механической энергии
- 64. Закон сохранения механической энергииЭнергия никогда не исчезает
- 65. МеханикаМЕХАНИКА ТВЕРДОГО ТЕЛА
- 66. Слайд 66
- 67. Слайд 67
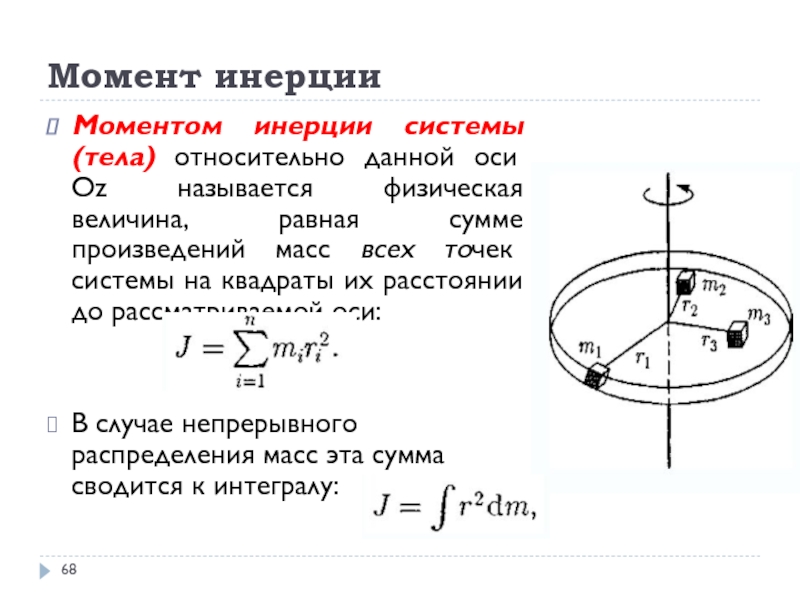
- 68. Момент инерцииМоментом инерции системы (тела) относительно данной
- 69. Теорема Штейнера: момент инерции тела J относительно
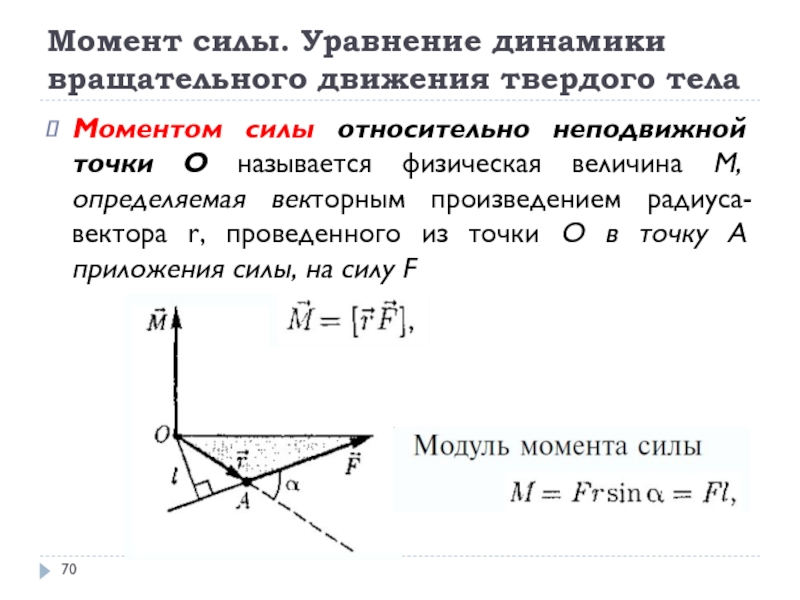
- 70. Момент силы. Уравнение динамики вращательного движения твердого
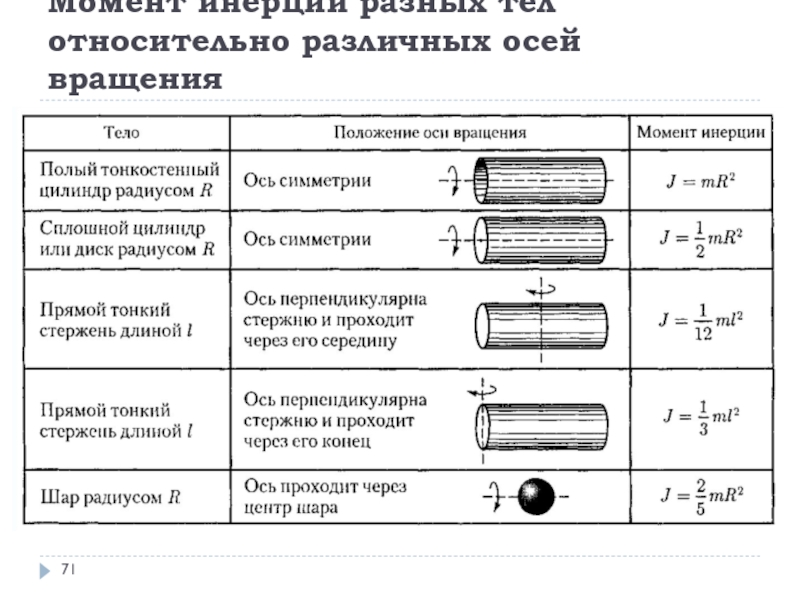
- 71. Момент инерции разных тел относительно различных осей вращения
- 72. Сравнение величин и уравнений поступательного и вращательного движения
- 73. Скачать презентанцию
ОСНОВНЫЕ РАЗДЕЛЫ ОБЩЕЙ ФИЗИКИмеханика термодинамика и молекулярная физикаэлектричество и магнетизмоптикаатомная физикаквантовая физикаядерная физика
Слайды и текст этой презентации
Слайд 2ОСНОВНЫЕ РАЗДЕЛЫ ОБЩЕЙ ФИЗИКИ
механика
термодинамика и молекулярная физика
электричество и магнетизм
оптика
атомная
физика
Слайд 3МЕХАНИКА
раздел физики, изучающий простейшую форму движения – механическое движение,
связанное с перемещением тела в пространстве и времени
Слайд 5Определение
Механика – раздел физики, в котором изучается механическое движение.
Механическое движение
– изменение положения данного тела(или частей тела) относительно других тел,
происходящее во времени и пространстве.
Слайд 6Механика Галилея — Ньютона называется классической механикой. В ней изучаются
законы движения макроскопических тел, скорости которых малы по сравнению со
скоростью света с в вакууме.Ограниченность применимости классической механики:
тела больших масс (по сравнению с массой атомов), движущихся с малыми скоростями (по сравнению со скоростью света).
Механика
Слайд 7Механика делится на три раздела:
1) кинематику; 2) динамику; 3) статику.
Кинематика
изучает движение тел, не рассматривая причины, которые это движение обусловливают.
Динамика
изучает законы движения тел и причины, которые вызывают или изменяют это движение.Статика изучает законы равновесия системы тел. Если известны законы движения тел, то из них можно установить и законы равновесия. Поэтому законы статики отдельно от законов динамики физика не рассматривает.
Механика
Слайд 9Кинематика поступательного движения
Материальная точка – тело, размеры которого несущественны(ими можно
пренебречь) в рамках какой-либо конкретной задачи.
Абсолютно твердое тело – тело,
у которого расстояние между любыми двумя его точками неизменно.
Слайд 10Кинематика поступательного движения
Любое движение твердого тела можно представить как комбинацию
поступательного и вращательного движений.
Поступательное движение — это движение, при котором
любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
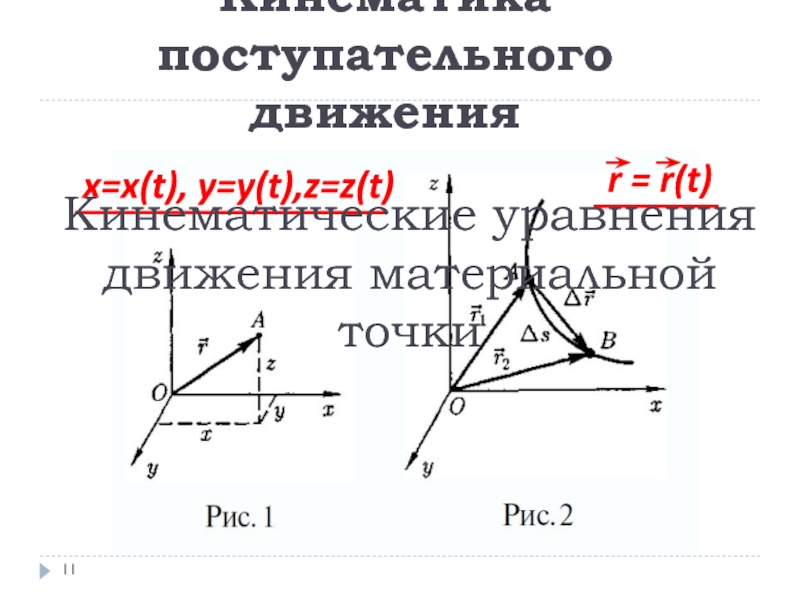
Слайд 11Кинематика поступательного движения
x=x(t), y=y(t),z=z(t)
r = r(t)
Кинематические уравнения
движения
материальной точки
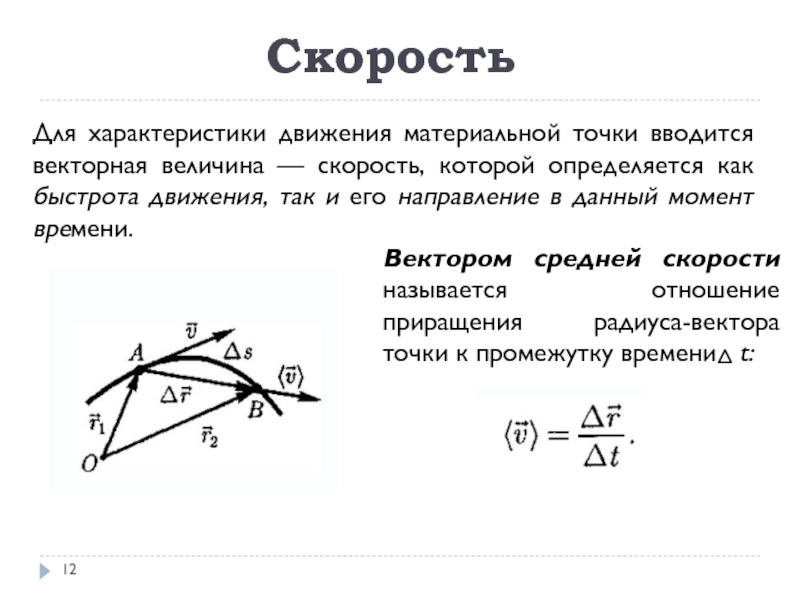
Слайд 12Скорость
Для характеристики движения материальной точки вводится векторная величина — скорость,
которой определяется как быстрота движения, так и его направление в
данный момент времени.
Слайд 13Скорость
При неограниченном уменьшении t средняя скорость стремится к предельному
значению, которое называется мгновенной скоростью v:
- модуль мгновенной скорости
Слайд 14 Пример
Половину времени тело двигалось со скоростью V1,
а вторую половину – со скоростью V2. Какова средняя скорость
тела?Решение
Вычислим суммарный путь, пройденный телом, обозначив t - общее время движения:
S = V1·t /2 + V2·t /2 = (V1 + V2) ·t /2.
Разделив на t, получаем среднюю скорость:
2. Изменим условие задачи. Половину пройденного расстояния тело двигалось со скоростью V1, а вторую половину – со скоростью V2. Какова средняя скорость тела?
Решение
Вычислим суммарное время движения: t = t1 + t2, где
t1 = S/(2·V1), t2 = S/(2·V2) – времена движения на 1 и 2 участках. Тогда
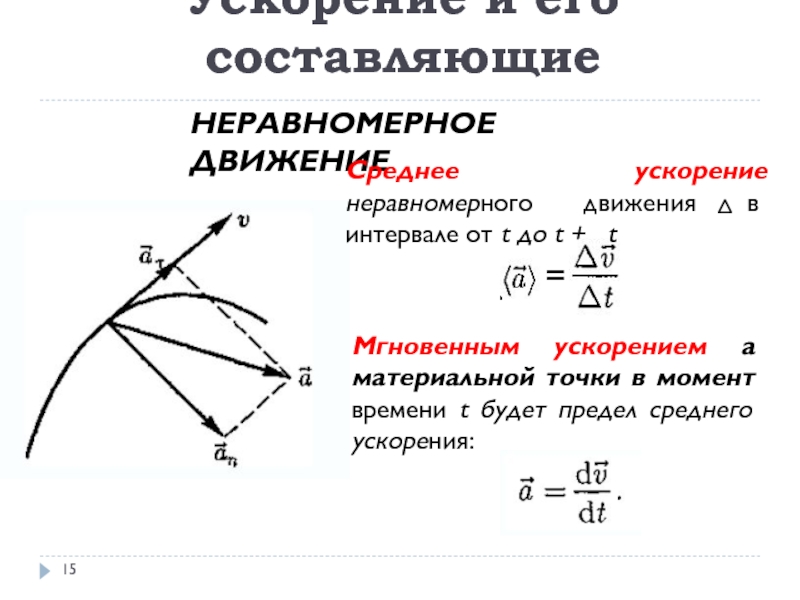
Слайд 15Ускорение и его составляющие
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
=
Среднее ускорение неравномерного движения в интервале
от t до t + t
Мгновенным ускорением а материальной
точки в момент времени t будет предел среднего ускорения:
Слайд 16Пример
Радиус-вектор материальной точки изменяется со временем по закону
,
где i, j - орты
осей х и у. Определить для момента времени t = 1 с: 1) модуль скорости ,
2) модуль ускорения.
Слайд 18Решение
Составляющие скорости: , следовательно,
модуль скорости равен
~ 6,7 м/с.
Ускорение равно первой производной скорости по времени:
Модуль ускорения равен:
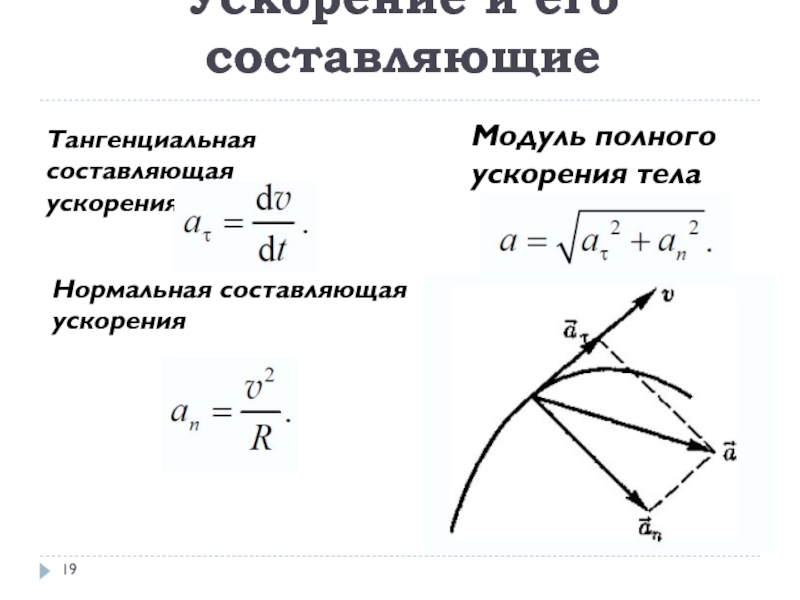
Слайд 19Тангенциальная составляющая
ускорения
Ускорение и его составляющие
Нормальная составляющая ускорения
Модуль полного ускорения тела
Слайд 20Ускорение и его составляющие
В зависимости от тангенциальной и нормальной составляющих
ускорения движение можно классифицировать следующим образом:
1) =
0, = О — прямолинейное равномерное движение;2) = а = const, = 0 — прямолинейное равнопеременное движение.
При таком виде движения
Длина пути, пройденного точкой, в случае равнопеременного движения
3) = f(t), = 0 — прямолинейное движение с переменным ускорением;
4) — 0, = const. При = 0 скорость изменяется только по направлению. Движение по окружности является равномерным.
Слайд 21ХАРАКТЕРИСТИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯ
Прямолинейное равномерное
Прямолинейное равноускоренное
Прямолинейное равнозамедленное
Равномерное движение по окружности
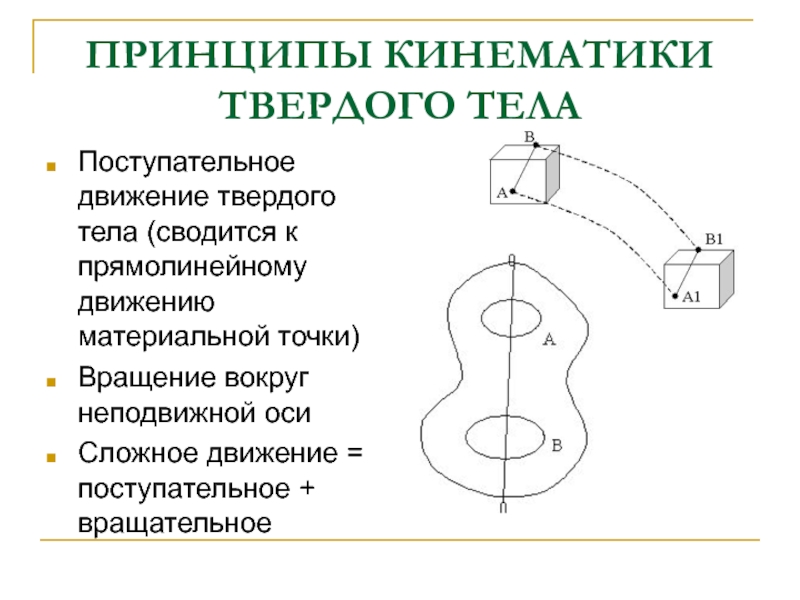
Слайд 23ПРИНЦИПЫ КИНЕМАТИКИ ТВЕРДОГО ТЕЛА
Поступательное движение твердого тела (сводится к прямолинейному
движению материальной точки)
Вращение вокруг неподвижной оси
Сложное движение = поступательное +
вращательное
Слайд 24Переход к вращательному движению
путь
скорость
ускорение
Равномерное движение
Равноускоренное движение
2 закон Ньютона
масса
Угол поворота
сила
Момент
сил
Угловое
ускорение
Угловая
скорость
Момент инерции
Кинематическая энергия
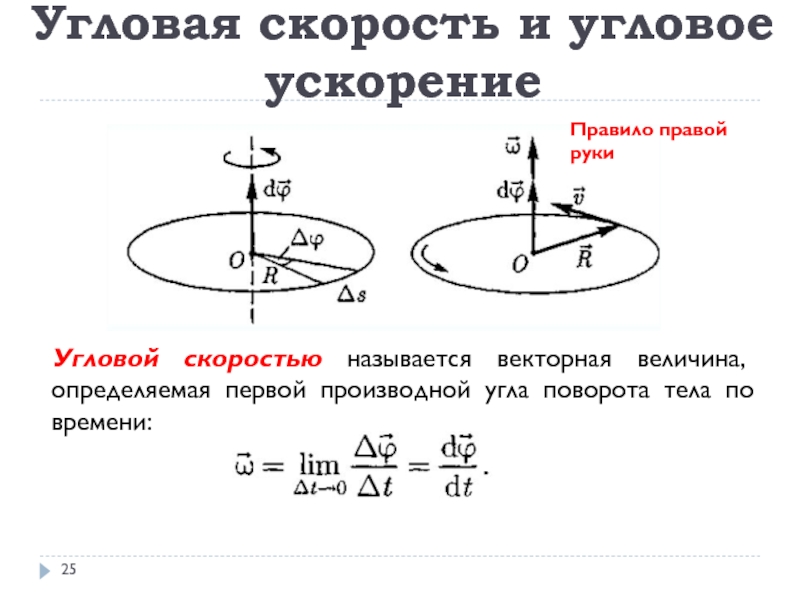
Слайд 25Угловой скоростью называется векторная величина, определяемая первой производной угла поворота
тела по времени:
Угловая скорость и угловое ускорение
Правило правой руки
Слайд 26Связь линейной скорости точки с угловой скоростью
Если = const,
то вращение равномерное и его можно характеризовать периодом вращения Т
— временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2 . Так как промежутку времени t = Т соответствуетУгловая скорость и угловое ускорение
Слайд 27Угловая скорость и угловое ускорение
Число полных оборотов, совершаемых телом при
равномерном его движении по окружности в единицу времени, называется частотой
вращения:Угловым ускорением называется векторная величина, определяемая первой производной угловой скорости по времени:
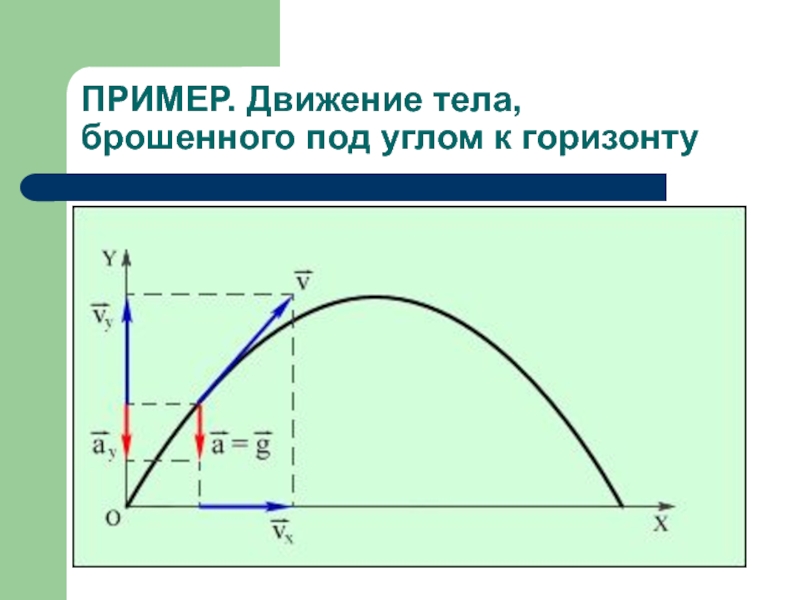
Слайд 29Пример
Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к
горизонту, если максимальная высота подъема тела равна 1/4 дальности его
полета.
Слайд 30Решение
Дано: h = 1/4s.
Найти: α.
Составляющие начальной скорости тела
v0x = v0cosα, v0y = v0sinα;
Ответ: α=450.
Слайд 31 Пример
Диск радиусом R = 10 см вращается равноускоренно с тангенциальным
ускорением at = 1,5 м/с2. Определить полное ускорение точки на
ободе диске в момент времени t = 2 c. Решение
Скорость точки в момент t = 2 c:
v = at·t = 1,5·2 = 3 м/с.
Нормальное ускорение в этот момент:
an = v2/R = 1,52/0,1 = 22,5 м/с2.
Полное ускорение определяем так:
Слайд 32Пример
Тело вращается вокруг неподвижной оси по закону, выражаемому формулой φ =
10 + 20t - 2t2.
Найти величину полного ускорения точки,
находящейся на расстоянии 0,1 м от оси вращения для момента времени t=4 с.
Слайд 34Пример
Закон движения материальной точки имеет вид
Определите модуль скорости и полное
ускорение материальной точки в момент времени t = 3 c.
Решение.
После
однократного дифференцирования получаем:
Слайд 35Еще раз дифференцируем:
Решения для модуля скорости и полного ускорения
при t = 3 c имеют
вид:
Слайд 38Основные понятия
Сила — это векторная величина, являющаяся мерой механического воздействия
на тело со стороны других тел или полей, в результате
которого тело приобретает ускорение или изменяет свою форму и размеры.Масса m – свойство тел, определяющее их бесконтактное взаимодействие с другими телами и инертность (способность сохранять скорость)..
Импульс тела (количество движения) – произведение массы тела на вектор его скорости:
Слайд 39Типы взаимодействия
Различные взаимодействия, известные в современной физике,
сводятся к четырем типам,
а именно:
1) гравитационное взаимодействие, возникающее между всеми телами, обладающими массой;
2)
электромагнитное взаимодействие между телами или частицами, обладающими электрическими зарядами;3) сильное взаимодействие, существующее, например, между частицами, из которых состоят ядра атомов;
4) слабое взаимодействие, характеризующее, например, процессы превращения некоторых элементарных частиц.
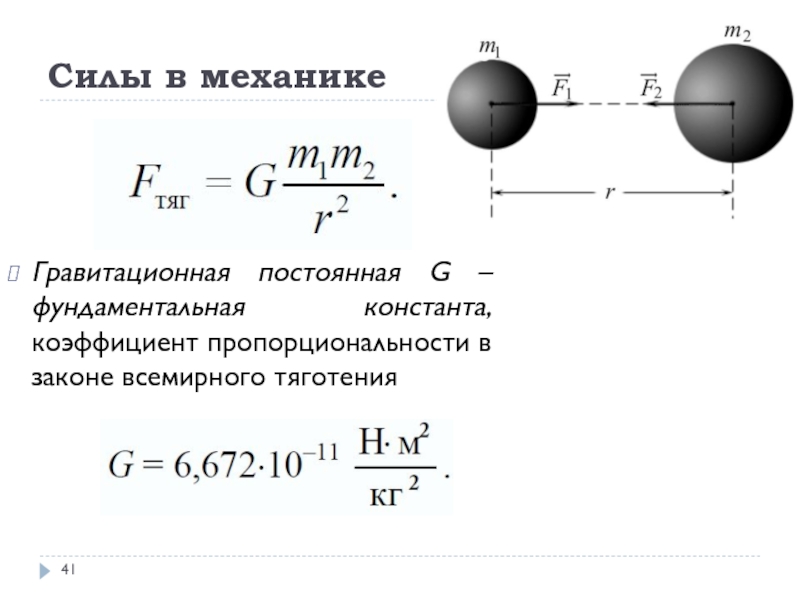
Слайд 40Силы в механике
В задачах механики учитываются гравитационные силы (силы тяготения)
и две разновидности электромагнитных сил – силы упругости и силы
реакции (нормальной реакции и трения).Силы тяготения – силы, возникающие между всеми телами в соответствии с законом всемирного тяготения Ньютона: между двумя материальными точками действуют силы взаимного притяжения, прямо пропорциональные массам этих точек и обратно пропорциональные квадрату расстояния между ними (эти силы направлены вдоль прямой, соединяющей данные материальные точки
Слайд 41Силы в механике
Гравитационная постоянная G – фундаментальная константа, коэффициент пропорциональности
в законе всемирного тяготения
Слайд 42Силы в механике
С каждым телом неразрывно связано гравитационное поле, проявляющееся
в том, что на помещенную в поле материальную точку действует
гравитационная сила, пропорциональная массе этой точки.Силовой характеристикой гравитационного поля является напряженность гравитационного поля (ускорение свободного падения) в данной точке пространства.
Сила, действующая на тело массой m со стороны гравитационного поля в точке с напряженностью g , называется силой тяжести:
Слайд 46Сила трения
Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение.
Внешним
трением называется трение, возникающее в плоскости касания двух соприкасающихся тел
при их относительном перемещении.Трение покоя (соприкасающиеся тела неподвижны относительно друг друга)
Трение скольжения
Трение качения
(происходит относительное перемещение этих тел)
Слайд 47Сила трения
Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение.
Внутренним
трением называется трение между частями одного и того же тела(между
различными слоями жидкости или газа, скорости которых меняются от слоя к слою).
Слайд 48Законы Ньютона
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние
покоя или равномерного прямолинейного движения до тех пор, пока воздействие
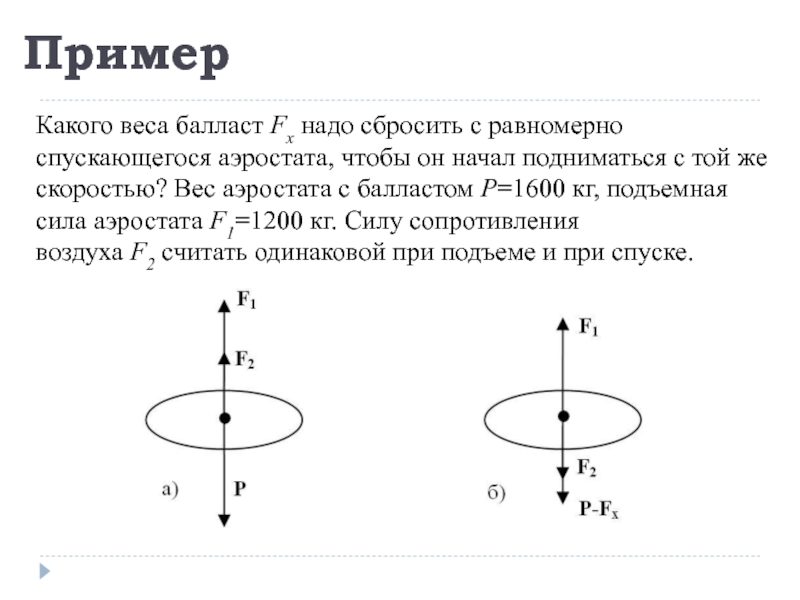
со стороны других тел не заставит ее изменить это состояние.
Слайд 49Пример
Какого веса балласт Fx надо сбросить с равномерно спускающегося аэростата, чтобы он
начал подниматься с той же скоростью? Вес аэростата с балластом Р=1600
кг, подъемная сила аэростата F1=1200 кг. Силу сопротивления воздуха F2 считать одинаковой при подъеме и при спуске.
Слайд 50Решение
Так как движение равномерное, то по первому закону Ньютона равнодействующая
сила равна нулю, т.е.
При спуске аэростата (рис. а) это
уравнение принимает вид:F1 + F2 - P = 0.
Когда балласт сброшен и аэростат начнет подниматься (рис. б), получим уравнение следующего вида:
F1 - F2 - (P - Fx) = 0.
Решая оба уравнения совместно, найдем вес балласта:
2F1 = 2P - Fx,
откуда Fx = 2P - 2F1 = 3200 кг - 2400 кг = 800 кг
У
О
Слайд 51Второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей
его силе, совпадает с нею по направлению и обратно пропорционально
массе материальной точки (тела).Законы Ньютона
Слайд 52Законы Ньютона
Третий закон Ньютона: всякое действие материальных точек (тел) друг
на друга носит характер взаимодействия; силы, с которыми действуют друг
на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
Слайд 53Закон сохранения импульса
Силы взаимодействия между материальными точками механической системы называются
внутренними.
Силы, с которыми на материальные точки системы действуют внешние тела,
называются внешними.Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной).
Слайд 54ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Импульс мат. точки – это векторная величина:
Система
материальных точек имеет импульс:
Импульс замкнутой системы материальных точек не
изменяется во времени
Слайд 56Энергия, работа, мощность
Изменение механического движения тела вызывается силами, действующими на
него со стороны других тел.
Чтобы количественно характеризовать процесс обмена энергией
между взаимодействующими телами, в механике вводится понятие работы силы.Единица работы — джоуль (Дж):
1 Дж = 1 Н • м
Слайд 57Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
За время dt
сила F совершает работу Fdr, и мощность, развиваемая этой силой,
в данный момент времениЕдиница мощности — ватт (Вт):
1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
Энергия, работа, мощность
Слайд 58Потенциальные силы в механике
Потенциальными (консервативными) называются силы, работа которых зависит
только от начального и конечного положения перемещающегося в пространстве тела
и не зависит от формы траектории. При замкнутой траектории работа потенциальной силы всегда равна нулю. Примерами потенциальных сил являются силы тяжести и упругости.Силы, работа которых зависит от формы траектории, называются непотенциальными. Примерами непотенциальных сил являются силы трения и сопротивления.
Система тел называется консервативной, если внутренние и внешние силы, действующие на тела системы, являются потенциальными, иначе система называется неконсервативной (диссипативной).
Слайд 59Потенциальная энергия —механическая энергия системы тел, определяемая их взаимным расположением
и характером сил взаимодействия между ними.
Потенциальная энергия тела массой m,
поднятого на высоту h над поверхностью ЗемлиКинетическая
и потенциальная энергии
Слайд 60Кинетическая
и потенциальная энергии
Кинетическая энергия механической системы — энергия механического движения
этой системы.
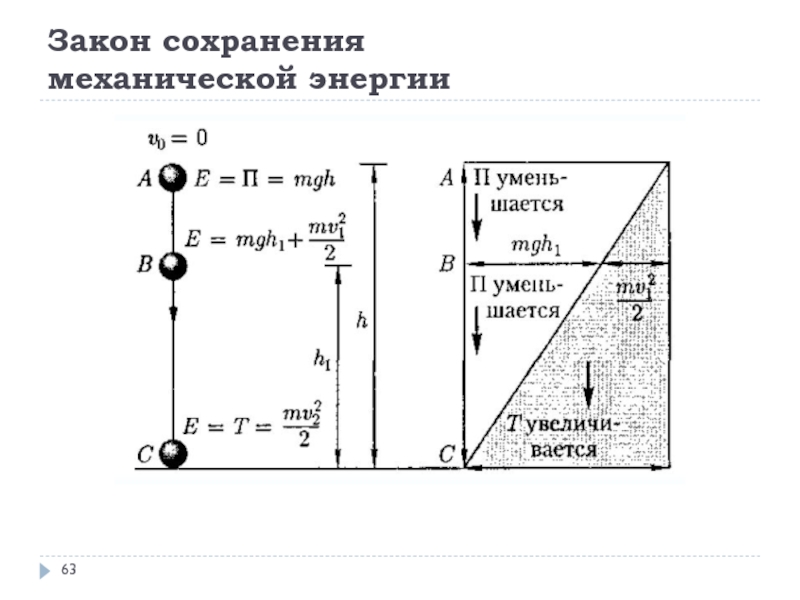
Слайд 62Закон сохранения
механической энергии
Закон сохранения механической энергии: в системе тел, между
которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.
е. не изменяется со временем.Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами.
Слайд 64Закон сохранения
механической энергии
Энергия никогда не исчезает и не появляется вновь,
она лишь превращается из одного вида в другой.
В этом
и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.
Слайд 68Момент инерции
Моментом инерции системы (тела) относительно данной оси Oz называется
физическая величина, равная сумме произведений масс всех точек системы на
квадраты их расстоянии до рассматриваемой оси:В случае непрерывного распределения масс эта сумма сводится к интегралу:
Слайд 69Теорема Штейнера: момент инерции тела J относительно произвольной оси равен
моменту его инерции Jс относительно параллельной оси, проходящей через центр
масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:Момент инерции
Слайд 70Момент силы. Уравнение динамики вращательного движения твердого тела
Моментом силы относительно
неподвижной точки О называется физическая величина М, определяемая векторным произведением
радиуса-вектора r, проведенного из точки О в точку A приложения силы, на силу F
