Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ 1. Основные понятия и определения молекулярной
Содержание
- 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ 1. Основные понятия и определения молекулярной
- 2. 1. Основные понятия и определения молекулярной физики
- 3. Равновесной, называется такая система, параметры
- 4. Процесс – переход из одного равновесного состояния
- 5. Идеальный газ – это газ для которого:
- 6. Давление. Основное уравнение молекулярно-кинетической теорииРассмотрим подробнее,
- 7. Слайд 7
- 8. Под скоростью необходимо понимать среднеквадратичную скорость
- 9. Следовательно, на другие стенки будет точно такое
- 10. Единицы измерения давления. По
- 11. Слайд 11
- 12. 1.Изохорический процесс. V
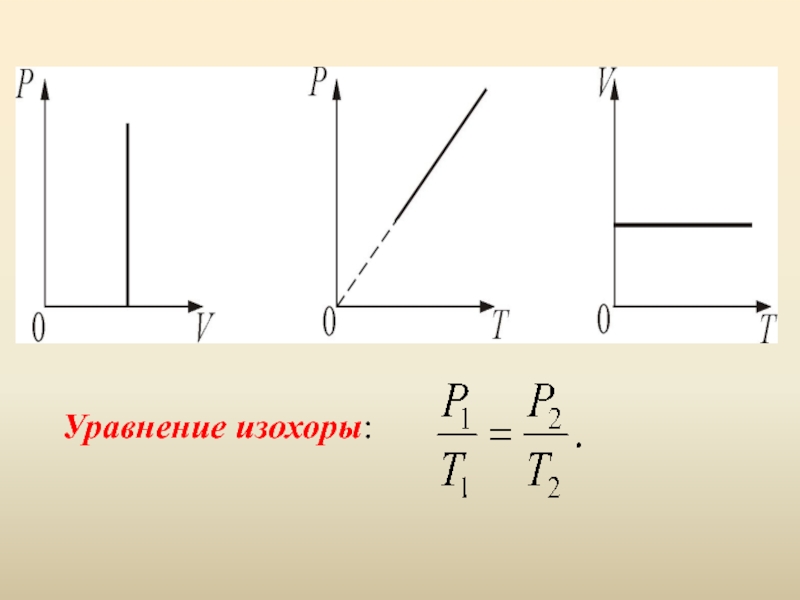
- 13. Уравнение изохоры:
- 14. 2. Изобарический процесс. Р = const.
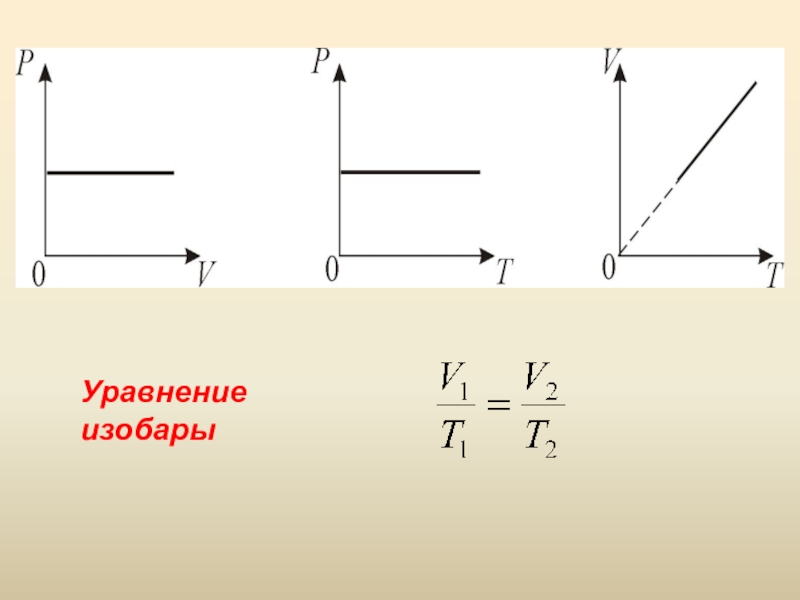
- 15. Уравнение изобары
- 16. 3. Изотермический процесс. T = const.
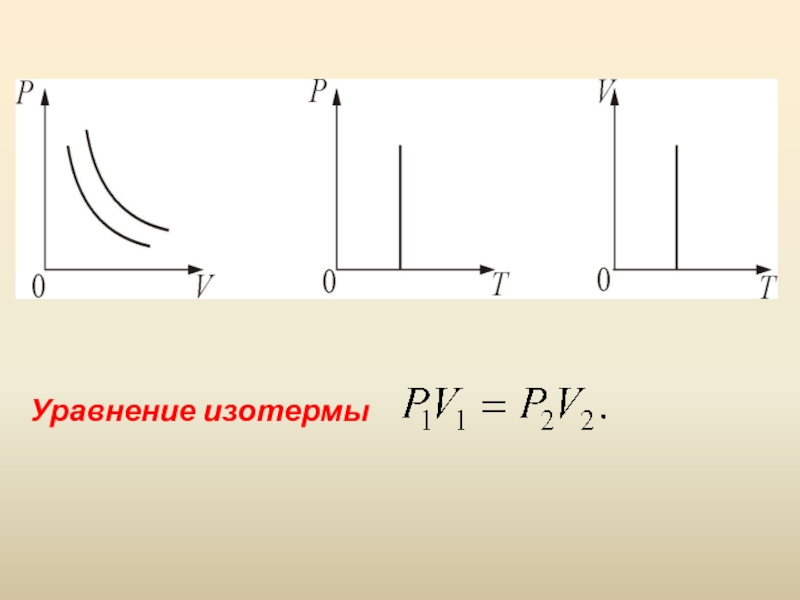
- 17. Уравнение изотермы
- 18. 4. Адиабатический процесс (изоэнтропийный). Процесс, происходящий
- 19. Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)Идеальным
- 20. Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака
- 21. Ещё в XIX веке Дж. Максвелл утверждал,
- 22. Молекулы движутся хаотически. Среди них есть и
- 23. Распределение молекул идеального газа по скоростям впервые
- 24. Скорость – векторная величина. Для проекции скорости
- 25. закон Максвелла – распределение молекул по абсолютным
- 26. Здесь – функция
- 27. При получаем
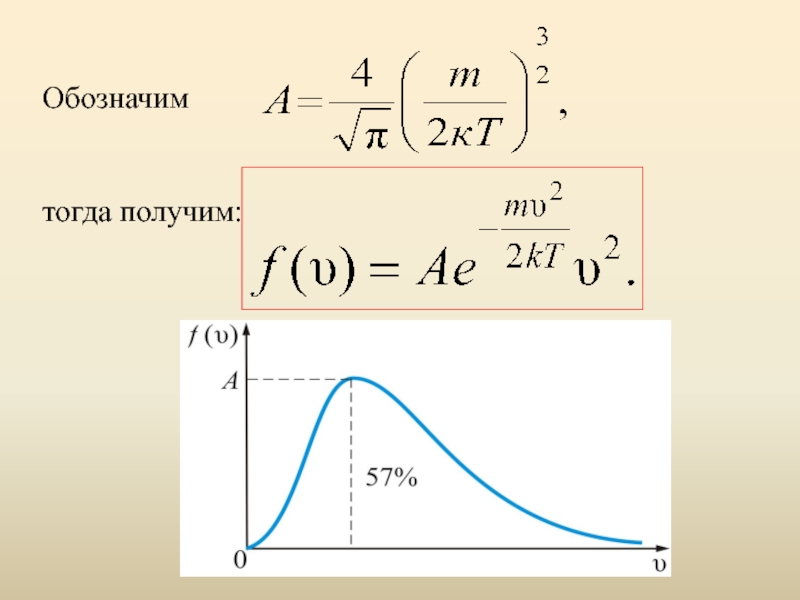
- 28. Обозначим
- 29. Выводы: - Вид распределения молекул газа
- 30. Из графика видно, что при «малых» υ
- 31. Величина скорости, на которую приходится максимум зависимости
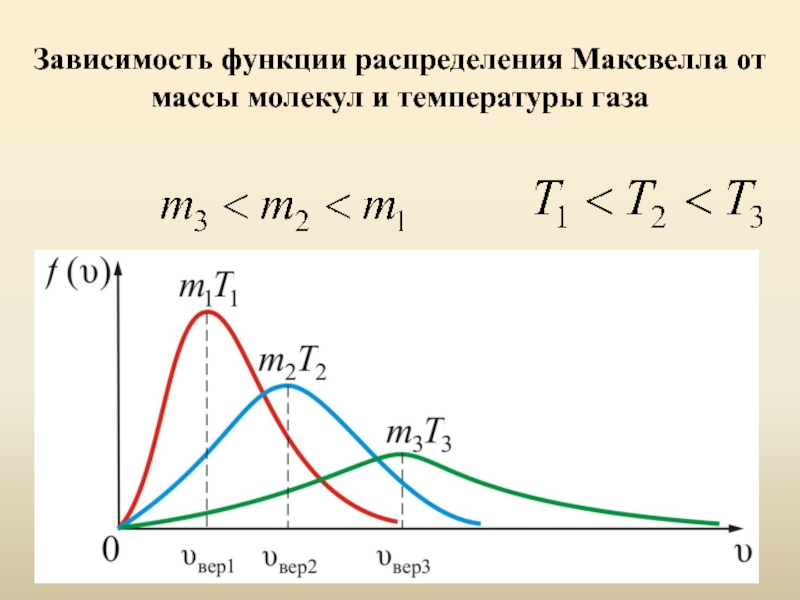
- 32. Зависимость функции распределения Максвелла от массы молекул и температуры газа
- 33. Площадь под кривой величина постоянная, равная единице
- 34. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИВнутренняя энергия. Работа и теплота2.Теплоёмкость
- 35. 1. Внутренняя энергия. Работа и теплотаНаряду с
- 36. В термодинамических процессах изменяется только кинетическая энергия
- 37. Внутренняя энергия U одного моля идеального газа
- 38. Понятно, что в общем случае термодинамическая система
- 39. Количество теплоты, сообщаемой телу, идёт на увеличение
- 40. 2. Теплоёмкость идеального газа Теплоёмкость
- 41. Удельная теплоёмкость Суд – количество теплоты,
- 42. Теплоёмкость термодинамической системы зависит от того, как
- 43. Если
- 44. Следовательно, проводимое тепло затрачивается и на нагревание
- 45. Это уравнение Майера для одного моля
- 46. Числом степени свободы называется
- 47. Многоатомная молекула может ещё и вращаться. Например,
- 48. i =6 i = 5i = 3
- 49. 4. Закон о равномерном распределении энергии по
- 50. Для молярной теплоемкости Для удельной теплоемкости
- 51. Если за цикл совершается положительная работа
- 52. В результате кругового процесса система возвращается в
- 53. Круговые обратимые и необратимые процессыКруговым процессом,
- 54. Все термодинамические процессы делят на две группы:
- 55. Тепловые машиныТепловой машиной называется периодический действующий
- 56. КПД тепловых двигателей
- 57. Идеальная тепловая машинаНаибольшим КПД при заданных температурах
- 58. Обязательными частями тепловой машины являются нагреватель (источник
- 59. Цикл, изученный Карно, является самым экономичным и
- 60. полезная работа
- 61. Второе начало термодинамики1. Невозможен процесс, единственным результатом
- 62. Слайд 62
- 63. Согласно Нернсту, изменение энтропии S стремится к
- 64. Третье начало термодинамики
- 65. Скачать презентанцию
1. Основные понятия и определения молекулярной физики и термодинамикиСовокупность большого числа частиц(атомов, молекул), составляющих макроскопическую систему, называется термодинамической системой.Система может находиться в различных состояниях. Величины, характеризующие состояние системы, называются параметрами состояния:
Слайды и текст этой презентации
Слайд 1МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ
1. Основные понятия и определения молекулярной физики и термодинамики
2.
Давление. Основное уравнение молекулярно-кинетической теории
идеального газа (уравнение Менделеева-Клапейрона)
Слайд 21. Основные понятия и определения молекулярной физики и термодинамики
Совокупность большого
числа частиц(атомов, молекул), составляющих макроскопическую систему, называется термодинамической системой.
Система может
находиться в различных состояниях. Величины, характеризующие состояние системы, называются параметрами состояния: давление P, температура T, объём V и так далее. Связь между P, T, V специфична для каждого тела и называется уравнением состояния.
Слайд 3
Равновесной,
называется такая система, параметры состояния которой одинаковы во
всех точках системы и не изменяются со временем (при неизменных
внешних условиях). При этом в равновесии находятся отдельные, макроскопические части системы
Слайд 4Процесс – переход из одного равновесного состояния в другое.
Релаксация –
возвращение системы в равновесное состояние.
Время релаксации – время перехода в
равновесное состояние.Если равновесие установилось, то система самопроизвольно не сможет выйти из него. Например, если опустить горячий камень в холодную воду, то, через некоторое время наступит равновесное состояние: температуры выровняются. Но обратный процесс невозможен – температура камня самопроизвольно не увеличится.
Слайд 5Идеальный газ – это газ для которого: 1) радиус
взаимодействия двух молекул много меньше среднего расстояния между ними (молекулы
взаимодействуют только при столкновении); 2) столкновения молекул между собой и со стенками сосуда – абсолютно упругие (выполняются законы сохранения энергии и импульса); 3) объем всех молекул газа много меньше объема, занятого газом.
Слайд 6 Давление. Основное уравнение молекулярно-кинетической теории
Рассмотрим подробнее, что представляет собой
один из основных параметров состояния – давление P.
Ещё в
XVIII веке Даниил Бернулли предположил, что давление газа – есть следствие столкновения газовых молекул со стенками сосуда.Именно давление чаще всего является единственным сигналом присутствия газа.
Слайд 7
Определим давление, как силу, действующую в единицу времени на единицу площади:
Молекулы имеют разные скорости, направленные в разные стороны, то есть скорости газовых молекул – случайная величина.
Более точно случайную величину характеризует среднеквадратичная величина.
Слайд 8Под скоростью необходимо понимать среднеквадратичную скорость Вектор скорости, направленный произвольно в пространстве,
можно разделить на три составляющих: Ни одной из этих проекций нельзя
отдать предпочтение из-за хаотичного теплового движения молекул, то есть в среднем
Слайд 9Следовательно, на другие стенки будет точно такое же давление.
Тогда
можно записать в общем случае:
где – средняя энергия одной молекулы.
Это основное уравнение молекулярно-кинетической теории газов.
Давление газов определяется средней кинетической энергией поступательного движения молекул.
Слайд 10 Единицы измерения давления. По определению,
поэтому размерность давления 1 Н/м2
= 1Па; 1 атм.= 9,8 Н/см2 = 98066 Па 105 Па 1 мм рт.ст. = 1 тор = 1/760 атм. = 133,3 Па 1 бар = 105 Па; 1 атм. = 0,98 бар.
Слайд 11
Законы идеальных газов
В XVII – XIX веках были сформулированы
опытные законы идеальных газовИзопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
Слайд 12
1.Изохорический процесс. V = const.
Изохорическим
процессом называется процесс, протекающий при постоянном объёме
V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля: P/Т = const :«При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным».
Слайд 14 2. Изобарический процесс. Р = const. Изобарическим процессом называется процесс,
протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе
подчиняется закону Гей-Люссака: V/T = const «При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным».
Слайд 16 3. Изотермический процесс. T = const. Изотермическим процессом называется процесс, протекающий
при постоянной температуре Т. Поведение идеального газа при изотермическом
процессе подчиняется закону Бойля-Мариотта: РV = const «При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным».
Слайд 184. Адиабатический процесс (изоэнтропийный). Процесс, происходящий без теплообмена с
окружающей средой. 5. Политропический процесс. Процесс, при
котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
Слайд 19
Уравнение состояния идеального газа
(уравнение Менделеева-Клапейрона)
Идеальным газом называют газ, молекулы
которого пренебрежимо малы, по сравнению расстояния между ними, и не
взаимодействуют друг с другом на расстоянии.Все газы, при нормальных условиях, близки по свойствам к идеальному газу. Ближе всех газов к идеальному газу – водород.
Уравнение, связывающее основные параметры состояния идеального газа вывел великий русский ученый Д.И. Менделеев.
Слайд 20Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и Шарля с
законом Авогадро. Уравнение, связывающее все эти законы, называется уравнением Менделеева-Клапейрона:
Для одного моля можно записать
Слайд 21Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно
сталкиваясь друг с другом, как-то «распределяются» по скоростям, причём вполне
определённым образом.Функция распределения Максвелла
Слайд 22Молекулы движутся хаотически. Среди них есть и очень быстрые, и
очень медленные. Благодаря беспорядочному движению и случайному характеру их взаимных
столкновений, молекулы определённым образом распределяются по скоростям. Это распределение оказывается однозначным и единственно возможным, и не только не противоречит хаотическому движению, но именно им и обусловлено.
Слайд 23Распределение молекул идеального газа по скоростям впервые было получено знаменитым
английским ученым Дж. Максвеллом в 1860 году с помощью методов
теории вероятностей.Максвелл Джеймс Клерк
(1831 – 1879) – английский физик.
Работы посвящены электродинамике, молекулярной физике, общей статике, оптике, механике, теории упругости. Установил статистический закон, описывающий распределение молекул газа по скоростям.
Слайд 25закон Максвелла – распределение молекул по абсолютным значениям скоростей:
где – доля всех частиц единичного объёма, скорости которых лежат в интервале от υ до
Слайд 26
Здесь – функция распределения молекул по
скоростям, - интервал значений скоростей., Физический смысл
f(υ) в том, что это отношение числа молекул, скорости которых лежат в определенном интервале скоростей, к общему числу молекул в единичном интервале скоростей:
Слайд 27 При получаем плотность вероятности, или функцию
распределения молекул по скоростям:
Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в единичном интервале скоростей, включающем данную скорость.
Слайд 29Выводы:
- Вид распределения молекул газа по скоростям, для каждого
газа зависит от массы m и температуры Т газа и
не зависит от давления P и объёма V газа.- В показателе степени стоит отношение, кинетической энергии, соответствующей данной скорости υ к средней энергии теплового движения молекул при данной температуре:
Значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии (показывает, какова вероятность при данной температуре иметь такое значение кинетической энергии).
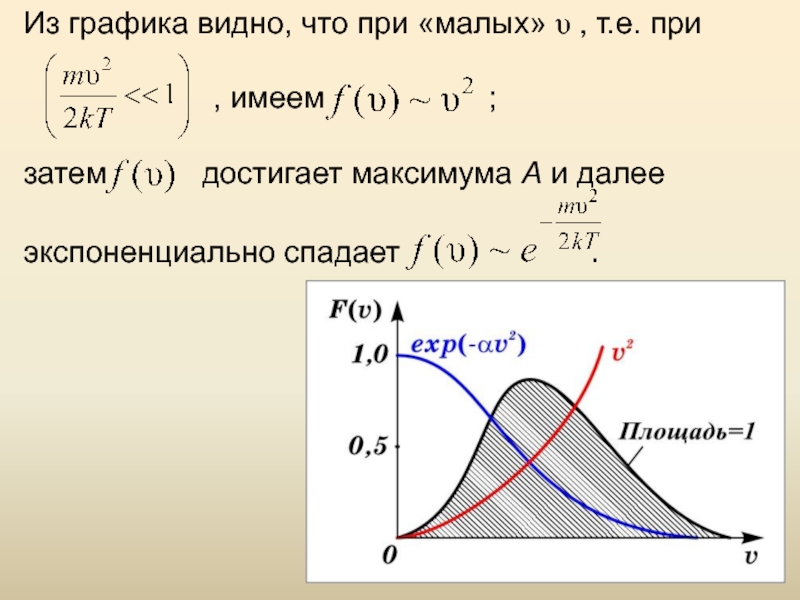
Слайд 30Из графика видно, что при «малых» υ , т.е. при
затем достигает максимума А и далее
экспоненциально спадает .
Слайд 31Величина скорости, на которую приходится максимум зависимости
называют наиболее вероятной скоростью.
Величину этой скорости найдем из условия равенства нулю производной
- наиболее вероятная скорость
одной молекулы. Для одного моля газа:
Слайд 33Площадь под кривой величина постоянная, равная единице (
), поэтому важно знать как будет изменяться положение максимума кривой: Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы только для газа в равновесной системе. Закон статистический и выполняется тем лучше, чем больше число молекул.
Слайд 34ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Внутренняя энергия. Работа и теплота
2.Теплоёмкость идеального газа. Уравнение
Майера
3. Теплоёмкости одноатомных и многоатомных газов
4. Закон о равномерном распределении
энергии по степеням свободы5. Применение первого начала термодинамики к изопроцессам идеальных газов
Слайд 351. Внутренняя энергия. Работа и теплота
Наряду с механической энергией любое
тело (или система) обладает внутренней энергией.
Она складывается
из теплового хаотического движения молекул,
потенциальной энергии их взаимного расположения,
- кинетической и потенциальной энергии электронов в атомах, нуклонов в ядрах и др
Слайд 36В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой
энергии недостаточно, чтобы изменить строение атома, а тем более ядра).
Следовательно,
фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул.
Слайд 37
Внутренняя энергия U одного моля идеального газа равна:
Таким образом, внутренняя энергия
зависит только от температуры.Внутренняя энергия U является функцией состояния системы
Слайд 38Понятно, что в общем случае термодинамическая система может обладать как
внутренней, так и механической энергией и разные системы могут обмениваться
этими видами энергии.Обмен механической энергией характеризуется совершённой работой А, а обмен внутренней энергией – количеством переданного тепла Q.
Слайд 39Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и
на совершение телом работы:
– это первое начало термодинамики или закон
сохранения энергии в термодинамике. 
Слайд 40 2. Теплоёмкость идеального газа
Теплоёмкость тела характеризуется количеством
теплоты, необходимой для нагревания этого тела на один градус
Размерность теплоемкости: [C] = Дж/К.
Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Слайд 41Удельная теплоёмкость Суд – количество теплоты, необходимое для нагревания
единицы массы вещества на 1 градус
[Cуд] = Дж/К. Молярная теплоемкость Сμ количество теплоты, необходимое для нагревания 1 моля газа на 1 градус [Cμ] = Дж/(мольК).
Слайд 42Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы
при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое
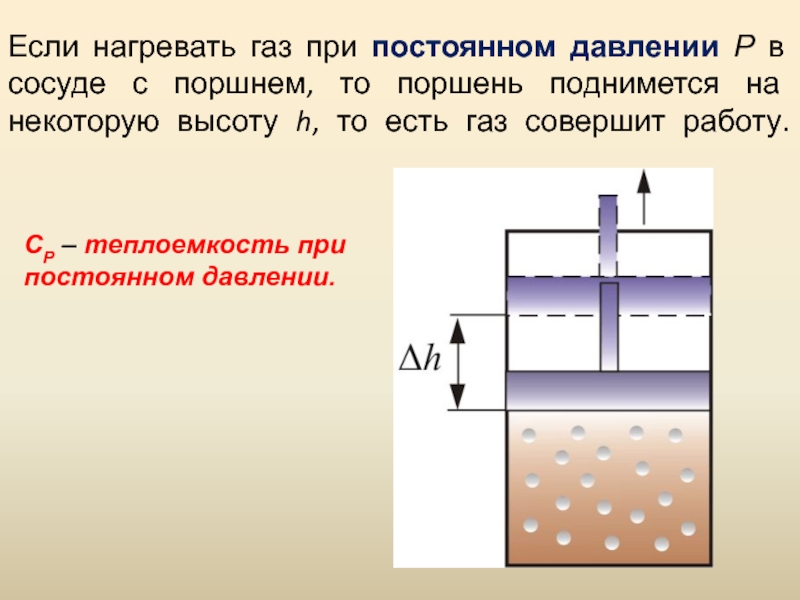
тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при постоянном объёме СV
Слайд 43 Если нагревать газ при постоянном давлении Р в
сосуде с поршнем, то поршень поднимется на некоторую высоту h,
то есть газ совершит работу.СР – теплоемкость при постоянном давлении.
Слайд 44Следовательно, проводимое тепло затрачивается и на нагревание и на совершение
работы. Отсюда ясно, что
Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Следовательно Q и С не являются функциями состояния. Величины СР и СV оказываются связанными простыми соотношениями.
Слайд 45 Это уравнение Майера для одного моля газа. Из него следует,
что физический смысл универсальной газовой постоянной в том, что R
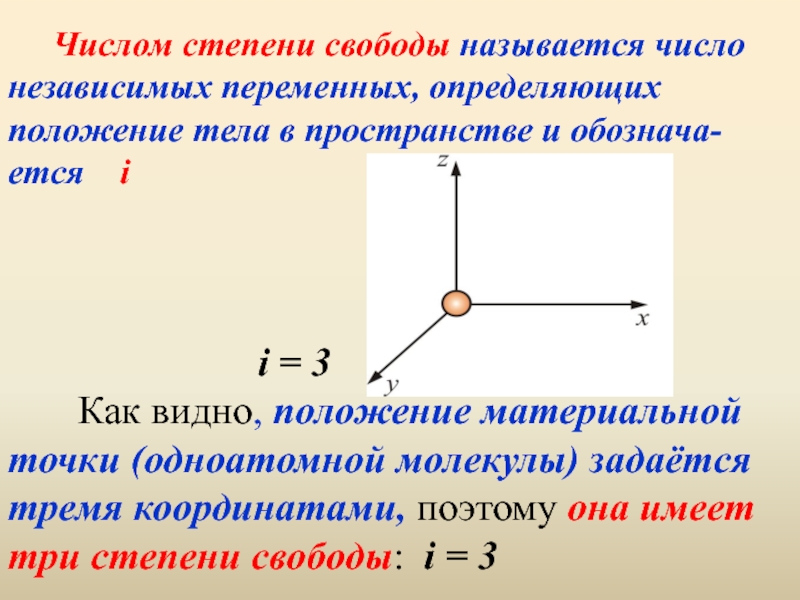
– численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
Слайд 46 Числом степени свободы называется число независимых переменных,
определяющих положение тела в пространстве и обознача-ется i i
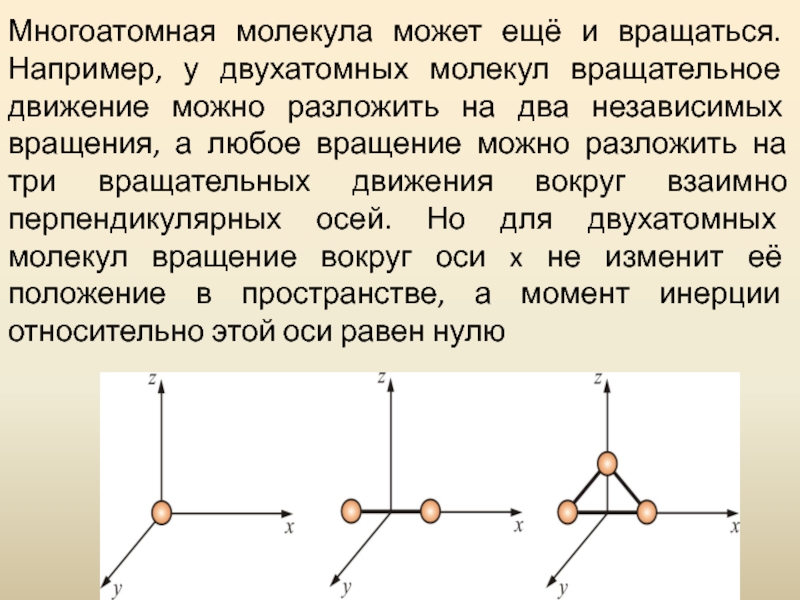
= 3 Как видно, положение материальной точки (одноатомной молекулы) задаётся тремя координатами, поэтому она имеет три степени свободы: i = 3
Слайд 47Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул
вращательное движение можно разложить на два независимых вращения, а любое
вращение можно разложить на три вращательных движения вокруг взаимно перпендикулярных осей. Но для двухатомных молекул вращение вокруг оси x не изменит её положение в пространстве, а момент инерции относительно этой оси равен нулю
Слайд 494. Закон о равномерном распределении энергии по степеням свободы
Больцман доказал,
что, средняя энергия, приходящаяся на одну степень свободы равна
Для i
степеней свободы i = iп + iвр + iкол
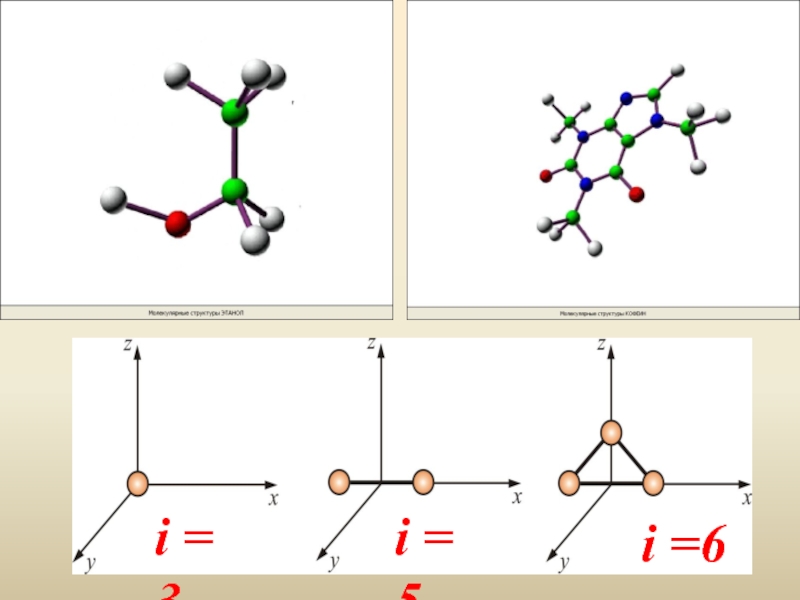
для одноатомной молекулы i = 3,
для двухатомной молекулы i = 5
для трёхатомной молекулы i = 6 
Слайд 51Если за цикл совершается положительная работа
(цикл протекает по часовой стрелке),
то он называется прямым
Если за цикл совершается отрицательная работа (цикл протекает против часовой стрелки),
то он называется обратным
Слайд 52В результате кругового процесса система возвращается в исходное состояние Термический коэффициент
полезного действия для кругового процесса
Q1 – количество теплоты, полученное
системой;
Q2 – количество теплоты, отданное системой 
Слайд 53 Круговые обратимые и необратимые процессы
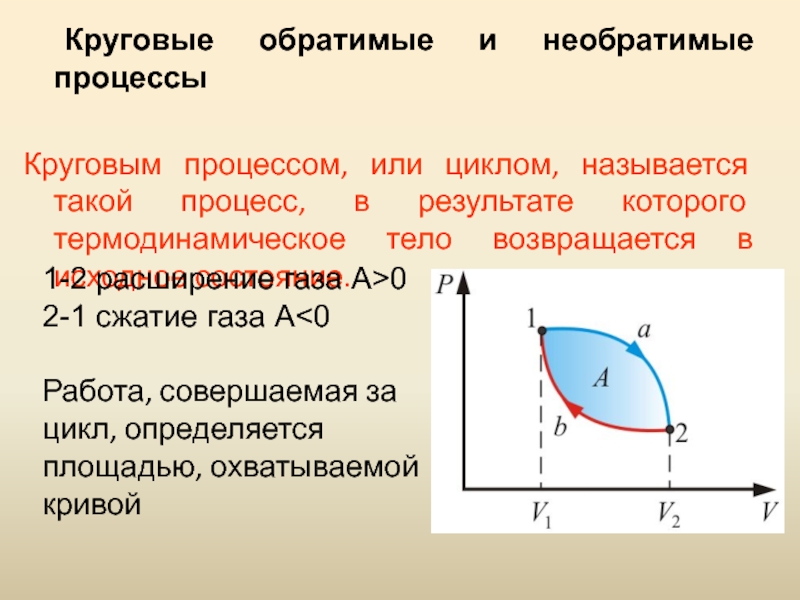
Круговым процессом, или циклом, называется
такой процесс, в результате которого термодинамическое тело возвращается в исходное
состояние.1-2 расширение газа А>0
2-1 сжатие газа A<0
Работа, совершаемая за цикл, определяется площадью, охватываемой кривой
Слайд 54Все термодинамические процессы делят на две группы: обратимые и необратимые.
Процесс называют обратимым, если он протекает таким образом, что после
окончания процесса он может быть проведен в обратном направлении через все те же промежуточные состояния, что и прямой процесс. Процесс называется необратимым, если он протекает так, что после его окончания систему нельзя вернуть в начальное состояние через прежние промежуточные состояния
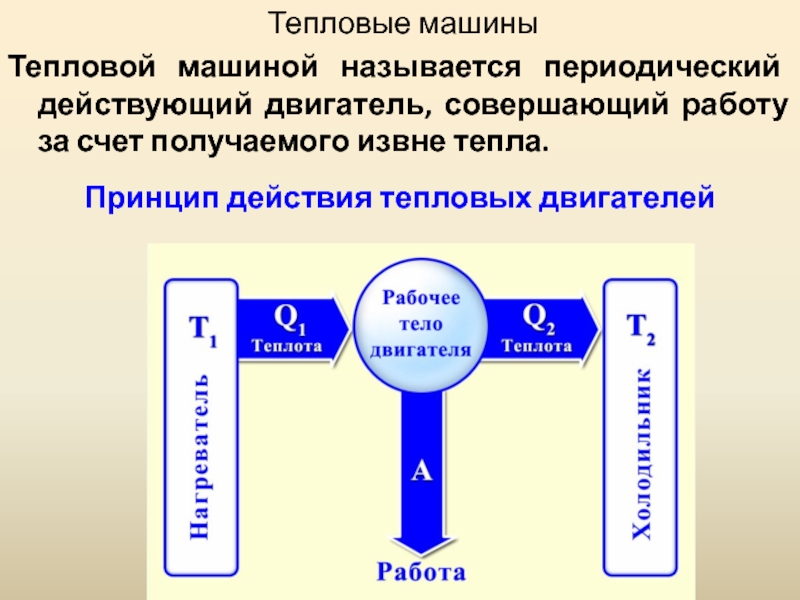
Слайд 55 Тепловые машины
Тепловой машиной называется периодический действующий двигатель, совершающий работу
за счет получаемого извне тепла.
Принцип действия тепловых двигателей
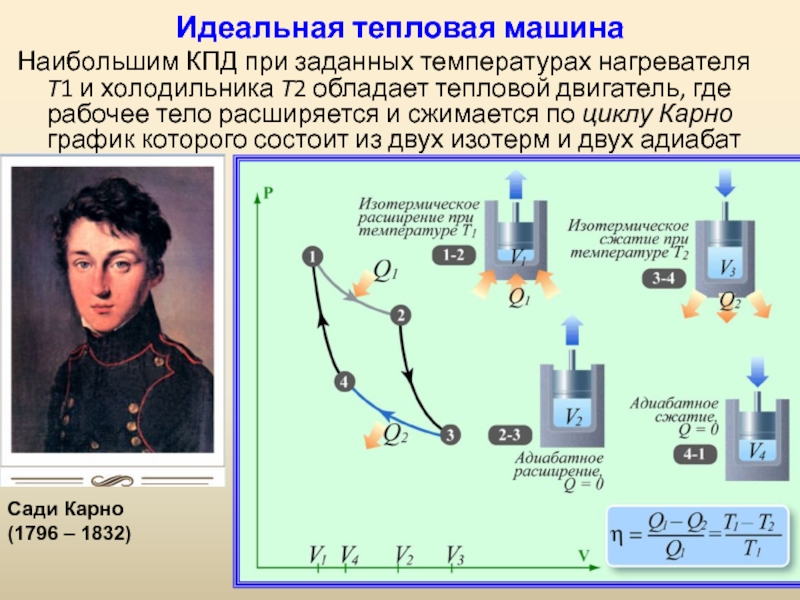
Слайд 57Идеальная тепловая машина
Наибольшим КПД при заданных температурах нагревателя T1 и
холодильника T2 обладает тепловой двигатель, где рабочее тело расширяется и
сжимается по циклу Карно график которого состоит из двух изотерм и двух адиабатСади Карно (1796 – 1832)
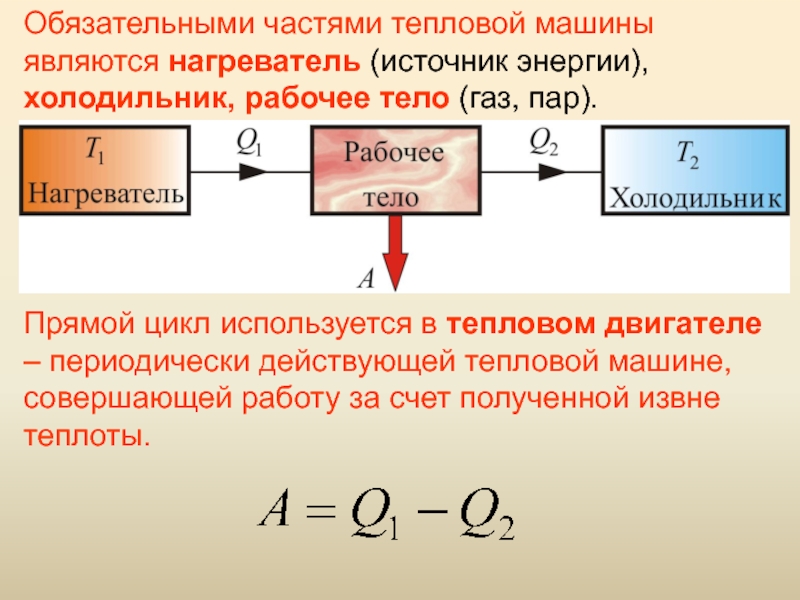
Слайд 58Обязательными частями тепловой машины являются нагреватель (источник энергии), холодильник, рабочее
тело (газ, пар).
Прямой цикл используется в тепловом двигателе – периодически
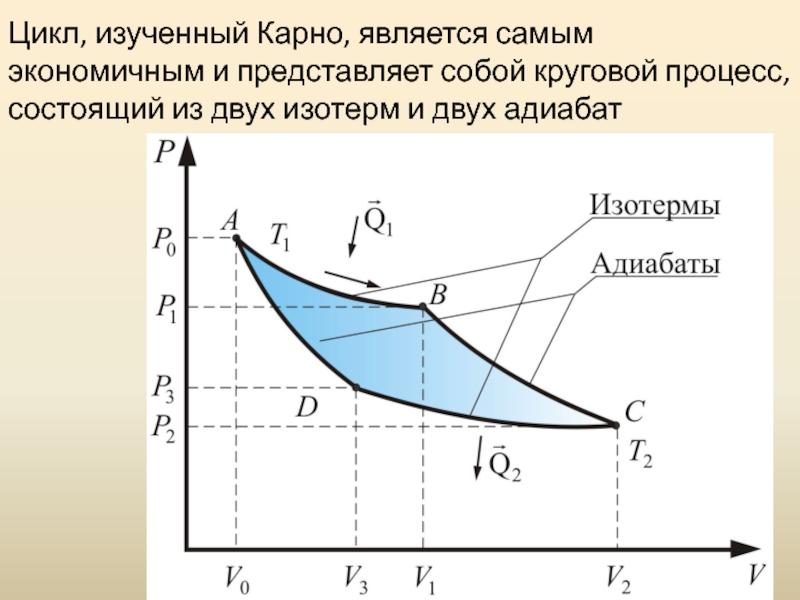
действующей тепловой машине, совершающей работу за счет полученной извне теплоты. 
Слайд 59Цикл, изученный Карно, является самым экономичным и представляет собой круговой
процесс, состоящий из двух изотерм и двух адиабат
Слайд 61Второе начало термодинамики
1. Невозможен процесс, единственным результатом которого является превращение
всей теплоты, полученной от нагревателя в эквивалентную ей работу (формулировка
Кельвина)2. Невозможен вечный двигатель второго рода (формулировка Томпсона-Планка).
3. Невозможен процесс, единственным результатом которого является передача энергии от холодного тела к горячему (формулировка Клаузиуса).
Слайд 62
Третье начало термодинамики
Недостатки первого и второго начал термодинамики в
том, что они не позволяют определить значение энтропии при абсолютном нуле Т = 0º К.На основании обобщения экспериментальных исследований свойств различных веществ при сверхнизких температурах был установлен закон, устранивший указанный недостаток. Сформулировал его в 1906 г. Нернст и называется он третьим началом термодинамики, или теоремой Нернста.
Слайд 63Согласно Нернсту, изменение энтропии S стремится к нулю при любых
обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах,
приближающихся к абсолютному нулю(S → 0 при Т → 0).
Энтропия любой равновесной системы при абсолютном нуле температуры может быть равна нулю.
Слайд 64
Третье начало термодинамики иногда формулируют следующим образом:
При абсолютном
нуле температуры любые изменения термодинамической системы происходят без изменения энтропии:
Следствием
третьего начала является то что, невозможно охладить тело до абсолютного нуля (принцип недостижимости абсолютного нуля температуры).
Иначе был бы возможен вечный двигатель II рода
