Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
НАВЧАЛЬНА ДИСЦИПЛІНА ПРИКЛАДНА КРИПТОГРАФІЯ Частина II ЗАБЕЗПЕЧЕННЯ ЦІЛІСНОСТІ
Содержание
- 1. НАВЧАЛЬНА ДИСЦИПЛІНА ПРИКЛАДНА КРИПТОГРАФІЯ Частина II ЗАБЕЗПЕЧЕННЯ ЦІЛІСНОСТІ
- 2. МОДУЛЬ № 5ВИКОРИСТАННЯ ХЕШ-ФУНКЦІЙ ДЛЯ ЗАБЕЗПЕЧЕННЯ ЦІЛІСНОСТІ ДАНИХ (ПОВІДОМЛЕНЬ)1
- 3. Лекція № 27ПРИНЦИПИ ПОБУДОВИ ХЕШ-ФУНКЦІЙ ДЛЯ ЗАБЕЗПЕЧЕННЯЦІЛІСНОСТІ ДАНИХ (ПОВІДОМЛЕНЬ)2
- 4. ПИТАННЯ ЛЕКЦІЇ № 271. Ітеративна хеш-функція2. Прості
- 5. 1. ІТЕРАТИВНА ХЕШ-ФУНКЦІЯ4
- 6. Усі криптографічні хеш-функції повин ні створювати дайджест
- 7. Функція стиску стискає n-бітовий вхідної рядок і
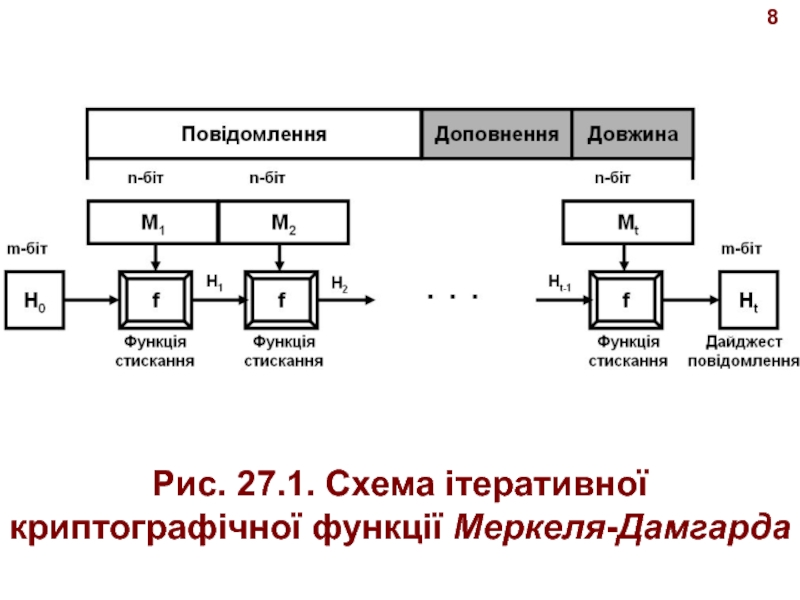
- 8. 1.1. Схема ітеративної криптографічної функціїМеркеля-Дамгарда (Merkle-Damgard)7 Схема Меркеля-Дамгарда
- 9. 8Рис. 27.1. Схема ітеративної криптографічної функції Меркеля-Дамгарда
- 10. 9 Схема використовує наступні кроки: 1. Довжина повідомлення й
- 11. 10 3. Перед стартом ітерації дайджест H0 установлюється
- 12. 11 Якщо функція стиску в схемі Меркеля-Дамгарда стійка
- 13. 12 У першому підході функція стиску зроблена на
- 14. 13 Ітеративна функція криптографічно го хешування може використовувати
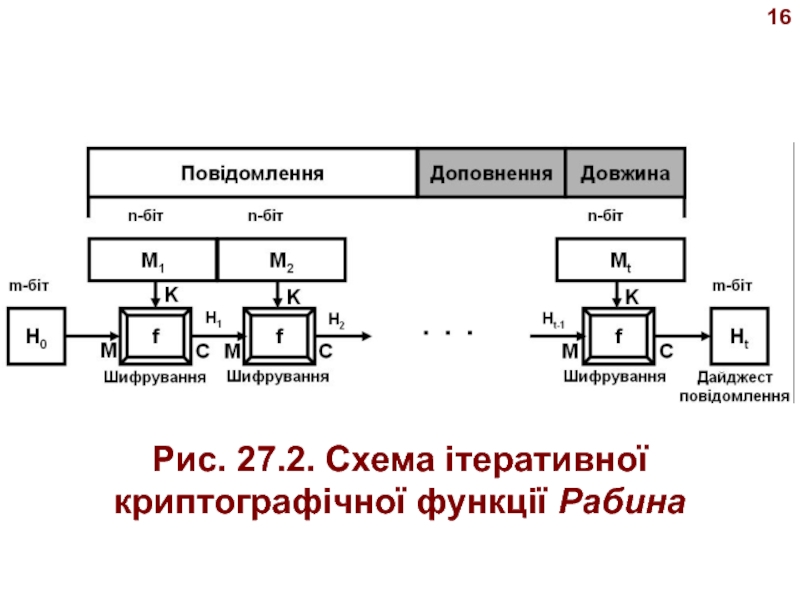
- 15. 14 Ітеративна хеш-функція, запропонова на Рабином, дуже проста. Схема
- 16. 15 Зашифрований текст - новий дайд-жест повідомлення. Зверніть увагу,
- 17. 16Рис. 27.2. Схема ітеративної криптографічної функції Рабина
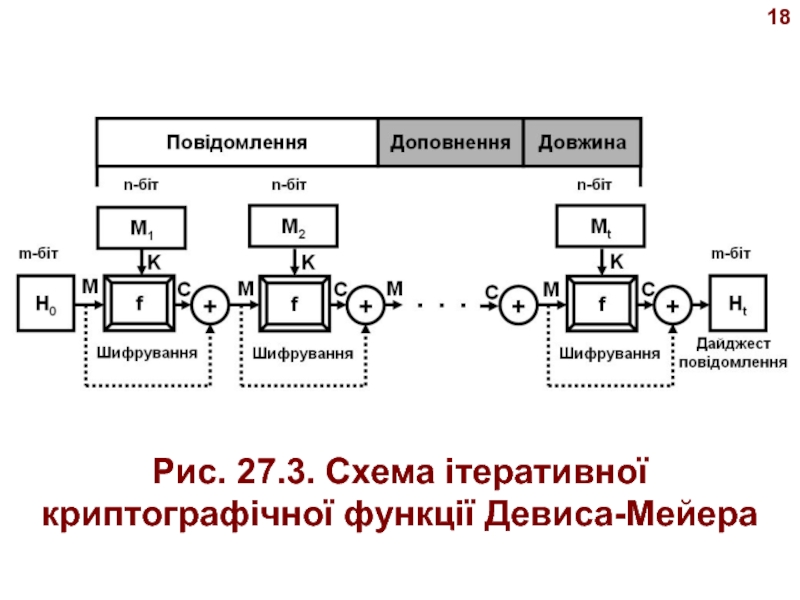
- 18. 171.3. Схема ітеративної криптографічної функції Девиса-Мейера (Davies-Mayer) Схема
- 19. 18Рис. 27.3. Схема ітеративної криптографічної функції Девиса-Мейера
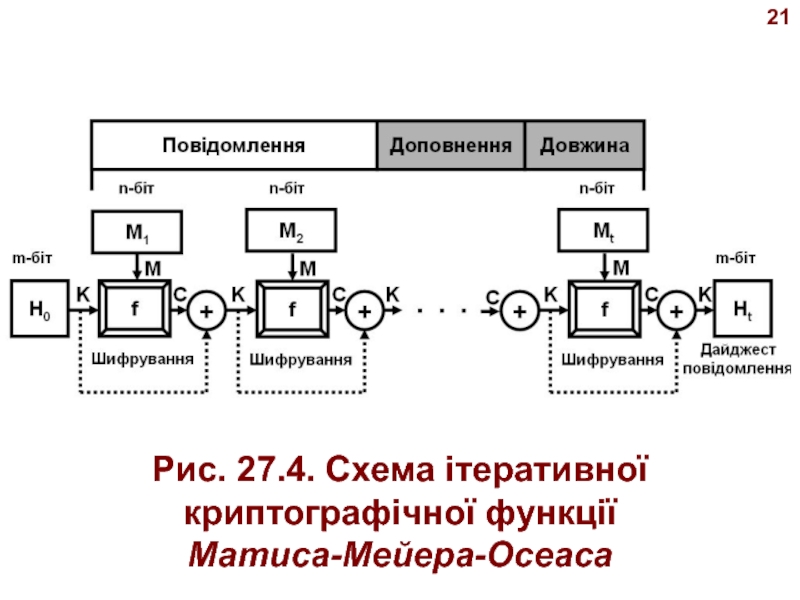
- 20. 19 Схема Матиса-Мейера-Осеаса (Metyas Mayer-Oseas) - це версія
- 21. 20 Наприклад, AES добре підходить для цієї мети. Схема показана на рис. 27.4.
- 22. 21Рис. 27.4. Схема ітеративної криптографічної функціїМатиса-Мейера-Осеаса
- 23. 22 Схема Миагучи-Пренеля - розширена версія схеми Матиса-Мейера-Осеаса. Щоб
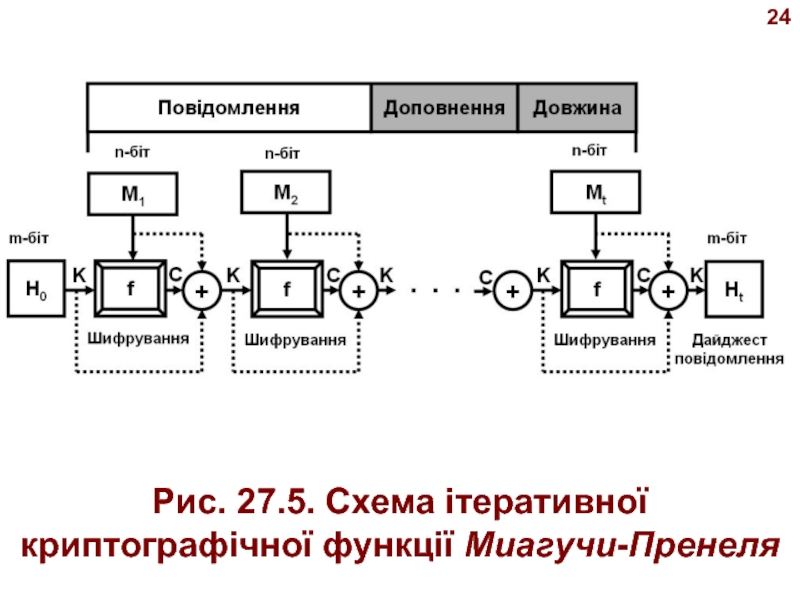
- 24. 23 Ця схема використовується в Whirlpool для створення геш-функции. На рис. 27.5 показана схема Миагучи-Пренеля.
- 25. Рис. 27.5. Схема ітеративної криптографічної функції Миагучи-Пренеля 24
- 26. ВИСНОВКИ 1. Усі функції криптографічного хешу вання повинні
- 27. ВИСНОВКИ 3. Множина ітеративних функцій криптографічного хешування використо
- 28. 272. ПРОСТІ ХЕШ-ФУНКЦІЇ
- 29. 28 Усі функції хешування побудовані на наступних загальних
- 30. 29де Сi - i-й біт хеш-коду, 1
- 31. 30Рис. 27.6. Проста функція хешування, що використовує операцію XOR
- 32. 31 Процедура здійснює простий побіто вий контроль парності
- 33. 32 1. Початкова ініціалізація n-бітового значення функції хешування
- 34. 33 Результатом процедури є "рандоміза ція" даних, що
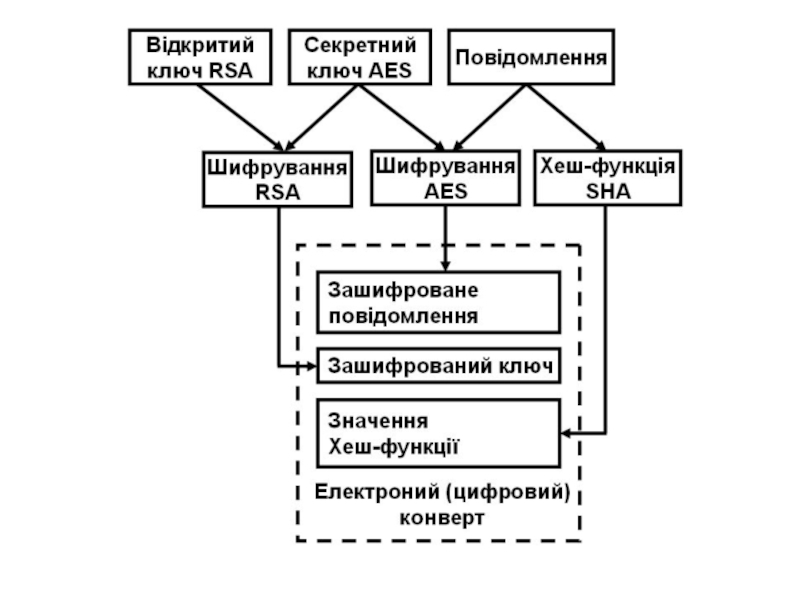
- 35. 343. ФОРМУВАННЯ ЕЛЕКТРОННОГО (ЦИФРОВОГО) КОНВЕРТА
- 36. 35 Як правило реалізації симетричних ал горитмів шифрування
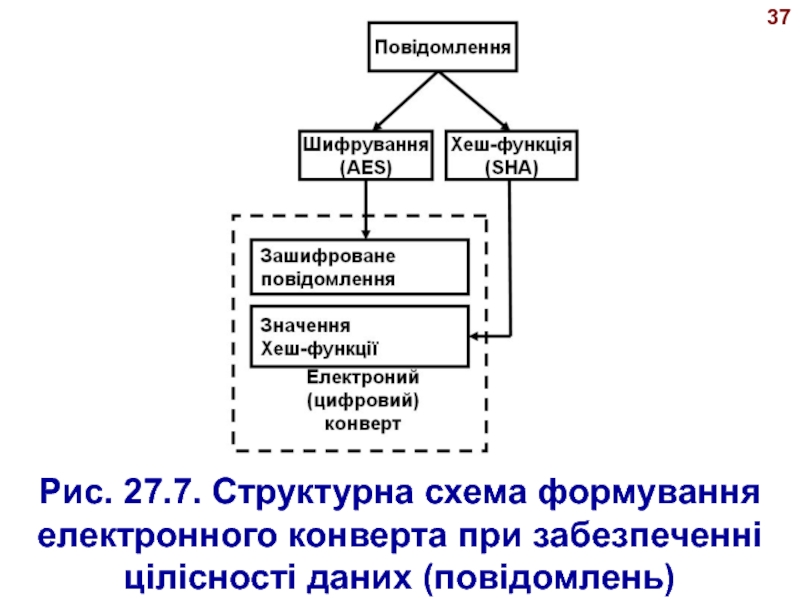
- 37. 36 Зашифроване повідомлення й значен ня дайджесту повідомлення
- 38. 37Рис. 27.7. Структурна схема формування електронного конверта при забезпеченні цілісності даних (повідомлень)
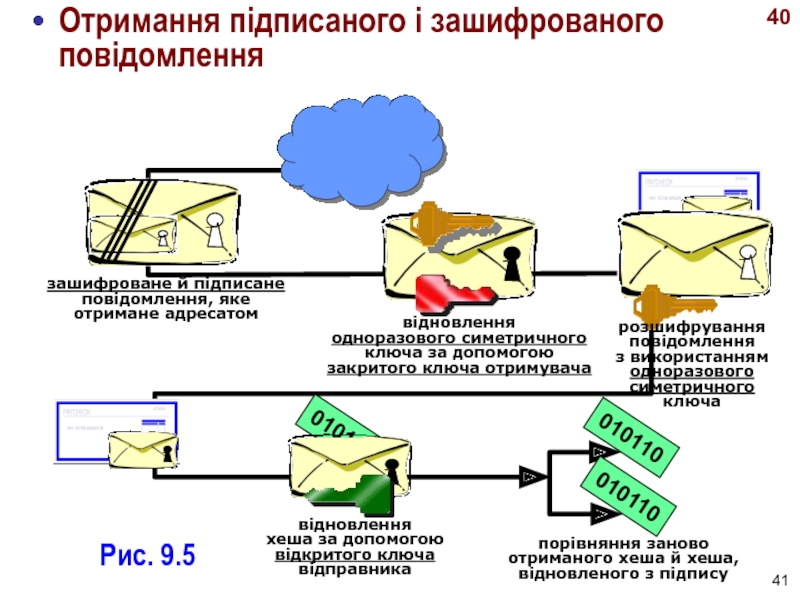
- 39. 38 Користувач, що одержав електронний конверт, розшифровує повідомлення
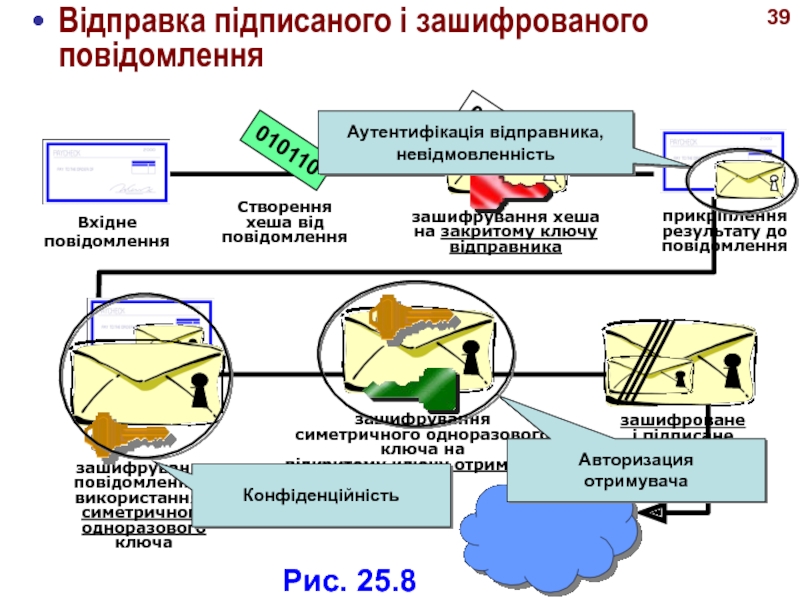
- 40. 39Відправка підписаного і зашифрованого повідомленняРис. 25.8
- 41. 40Рис. 9.5Отримання підписаного і зашифрованого повідомлення
- 42. Слайд 42
- 43. Скачать презентанцию
МОДУЛЬ № 5ВИКОРИСТАННЯ ХЕШ-ФУНКЦІЙ ДЛЯ ЗАБЕЗПЕЧЕННЯ ЦІЛІСНОСТІ ДАНИХ (ПОВІДОМЛЕНЬ)1
Слайды и текст этой презентации
Слайд 1НАВЧАЛЬНА ДИСЦИПЛІНА
ПРИКЛАДНА КРИПТОГРАФІЯ
Частина II
ЗАБЕЗПЕЧЕННЯ ЦІЛІСНОСТІ ТА АУТЕНТИЧНОСТІ ДАНИХ
Слайд 4ПИТАННЯ ЛЕКЦІЇ № 27
1. Ітеративна хеш-функція
2. Прості хеш-функції
3. Формування електронного
(цифрового) конверту
Слайд 6 Усі криптографічні хеш-функції повин ні створювати дайджест фіксованого розмі ру
з повідомлення змінного розміру.
Застосовувати таку функцію найкраще, використовуючи ітерацію.
Замість хеш-функції
з веденням змін ного розміру створена й використовується необхідна кількість раз функція з веденням фіксованого розміру, називана функцією стиску (стискання).5
Слайд 7 Функція стиску стискає n-бітовий вхідної рядок і створює m-бітовий рядок,
де n завжди більше чому m.
Ця схема відома як ітеративна
крипто графічна функція.6
Слайд 81.1. Схема ітеративної криптографічної функції
Меркеля-Дамгарда (Merkle-Damgard)
7
Схема Меркеля-Дамгарда - ітеративна хеш-функція,
яка є функцією стиску, стійкої до колізії. Схема показана на
рис. 27.1.
Слайд 109
Схема використовує наступні кроки:
1. Довжина повідомлення й доповнен ня додаються
в кінець повідомлення, щоб створити збільшене повідомлення, яке мо же
бути рівномірно розділене на n-бітові блоки; тут n - розмір блоку, який буде об роблений функцією стиску.2. Повідомлення тоді розглядають як t блоків, розмір кожного складається з n біт. Ми позначимо кожний блок М1, ..., Мt.
Ми позначаємо дайджест, створений при t ітераціях, - H1, H2, .... , Ht.
Слайд 1110
3. Перед стартом ітерації дайджест H0 установлюється на фіксоване значення,
звичайно називане IV (початкове значення або початковий вектор).
4. Функція стиску
при кожній ітерації обробляє Hi-1 і М, створюючи новий Hi.Інакше кажучи, ми маємо
Hi = f (Hi-1, Мi),
де f - функція стиску.
5. Ht - функція криптографічного хе шування первісного повідомлення, тобто h(M).
Слайд 1211
Якщо функція стиску в схемі Меркеля-Дамгарда стійка до колізії, хеш-функція
та кож стійка до колізії.
Схема Меркеля-Дамгарда сьогодні – підстава для
багатьох функцій криптогра фічного хешування. Єдина річ, яку ми по винні зробити, - розробити функцію стис ку, яка є стійкою до колізій, і вставити її в схему Меркеля-Дамгарда.Існує тенденція використовувати два різні підходи в розробці хеш-функції.
Слайд 1312
У першому підході функція стиску зроблена на "порожньому місці": вона
розроблена тільки для цієї мети.
У другому підході блоковий шифр із
симетричними ключами служить функцією стиску.Множина ітеративних функцій крип тографічного хешування використовує функції стиску, які зроблені "на порожньо му місці".
Ці функції стиску спеціально створені для цілей, яким вони служать.
Слайд 1413
Ітеративна функція криптографічно го хешування може використовувати бло ковий шифр
із симетричними ключами як функцію стиску.
Основна ідея такого підходу
- є кілька безпечних блокових шифрів із симетрич ними ключами, таких як трикратний DES, AES або ГОСТ, які можуть використовува тися для створення однобічної функції за-мість того, щоб створювати нову функцію стиску.Блоковий шифр у цьому випадку тіль ки виконує шифрування.
Слайд 1514
Ітеративна хеш-функція, запропонова на Рабином, дуже проста.
Схема Рабина базується на
схемі Мер келя-Дамгарда.
Функція стиску заміняється будь-яким алгоритмом шифрування. Блок повідом
лення використовується як ключ; попе редньо створений дайджест використо вується як вихідний текст.1.2. Схема ітеративної криптографічної функції Рабина
Слайд 1615
Зашифрований текст - новий дайд-жест повідомлення.
Зверніть увагу, що розмір дайджесту
- це розмір блокового шифру даних в ос новній криптографічній
системі.Наприклад, якщо DES використо вується як блоковий шифр, розмір дайд жесту - тільки 64 біта.
Хоча схема дуже проста, вона може бу-ти розкрита за допомогою атаки "відомості до середини", оскільки супротивник може застосувати алгоритм дешифрування крип тографічної системи.
Рис. 27.2 показує схему Рабина.
Слайд 1817
1.3. Схема ітеративної криптографічної функції Девиса-Мейера (Davies-Mayer)
Схема Девиса-Мейера (Davies-Mayer) в
основному повторює схему Рабина, за ви нятком того, що використовує
прямий зв'я зок для захисту від атаки "відомості по се редині".Схема показана на рис. 27.3.
Слайд 2019
Схема Матиса-Мейера-Осеаса (Metyas Mayer-Oseas) - це версія схеми Девиса -Мейера:
блоки повідомлення застосо вуються як ключі криптосистеми. Схема може бути
використана, якщо блоки даних і ключ шифрування мають той самий роз мір.1.4. Схема ітеративної криптографічної функції Матиса-Мейера-Осеаса
(Metyas-Mayer-Oseas)
Слайд 2322
Схема Миагучи-Пренеля - розширена версія схеми Матиса-Мейера-Осеаса.
Щоб зробити алгоритм більш
стійким до атаки, вихідний текст, ключ шифру й зашифрований текст
складаються за допо-могою xor й створюють новий дайджест.1.5. Схема ітеративної криптографічної функції Миагучи-Пренеля
Слайд 2423
Ця схема використовується в Whirlpool для створення геш-функции.
На рис. 27.5
показана схема Миагучи-Пренеля.
Слайд 26ВИСНОВКИ
1. Усі функції криптографічного хешу вання повинні створювати дайджест фіксо
ваного розміру з повідомлення змінного розміру. Створення такої функції найкраще
може бути досягнуте застосуванням ітера ції.2. Схема Меркеля-Дамгарда (Merkle Damgard) - ітеративна функція крипто графічного хешування, стійка до колізій, якщо при цьому функція стиску стійка до колізій.
25
Слайд 27ВИСНОВКИ
3. Множина ітеративних функцій криптографічного хешування використо вують функції стиску,
які зроблені на "по рожньому місці". Ці функції стиску спе
ціально розроблені для цієї мети, яку вони обслуговують.4. Ітеративна функція криптогра фічного хешування може використовувати блоковий шифр із симетричними ключами замість функції стиску.
26
Слайд 2928
Усі функції хешування побудовані на наступних загальних принципах.
Значення, що вводиться
(повідомлен ня, файл і т.п.) розглядається як послі довність n-бітових
блоків.Дані, що вводяться, обробляються послідовно блок за блоком, щоб у резуль таті одержати n-бітове значення функції хе шування.
Однієї з найпростіших функцій хешу вання є зв'язування всіх блоків операцією xor (порозрядного "виключаючого АБО").
,
Слайд 3029
де Сi - i-й біт хеш-коду, 1 ≤ i ≤
n;
m - число n-бітових блоків вводу;
bij - i-й біт в
j-м блоці;- операція xor.
Схема процедури показана на рис. 27.6.
Це можна записати в наступному виді:
Слайд 3231
Процедура здійснює простий побіто вий контроль парності й звичайно нази
вається поздовжнім контролем парності. Така процедура виявляється досить ефективної для
контролю цілісності даних довільного виду.Найпростіше вдосконалити таку схему, розглянувши можливість виконання одно бітового циклічного зсуву (повороту) зна чення функції хешування після завершення обробки кожного чергового блоку.
Така процедура складається з наступ них етапів.
Слайд 3332
1. Початкова ініціалізація n-бітового значення функції хешування нульовим зна ченням.
2.
Послідовна обробка n-бітових бло ків даних за наступним правилом.
3. Виконання
циклічного зсуву поточ ного значення функції хешування вліво на один біт.4. Додавання поточного блоку до зна чення функції хешування за допомогою операції xor.
Слайд 3433
Результатом процедури є "рандоміза ція" даних, що вводяться і руйнування
ре гулярності, яка може мати для них місце.
Слайд 3635
Як правило реалізації симетричних ал горитмів шифрування (DES, IDEА й
т.п.) є досить швидкими на відміну від реалізацій алгоритмів з
відкритими ключами (неси метричних).Тому при передачі повідомлень вони зашифровуються за допомогою симетрич ного алгоритму й секретного ключа (нап риклад, алгоритму AES).
З використанням вихідного повідом лення визначається хеш-функція (дайджест повідомлення), наприклад з використанням хеш-функції SHA.
Слайд 3736
Зашифроване повідомлення й значен ня дайджесту повідомлення (значення хеш функції)
розміщуються в одному електрон ному конверті (документі) і відправляються тому
для якого він призначений (рис. 27.7).
Слайд 3837
Рис. 27.7. Структурна схема формування електронного конверта при забезпеченні цілісності
даних (повідомлень)
Слайд 3938
Користувач, що одержав електронний конверт, розшифровує повідомлення за до помогою
секретного ключа.
Далі обчислює з його допомогою хеш -функцію й звіряє
обчислене значення хеш -функції з отриманим значенням в електрон ному конверті.
