Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нечеткие множества
Содержание
- 1. Нечеткие множества
- 2. Нечеткие множестваВ работе Лотфи А. Заде «Fuzzy
- 3. Нечеткие множестваНаиболее распространенным является суждение, предложенное в
- 4. Нечеткие множестваВ случае, когда А - некоторое
- 5. Методы построения функции принадлежности:Пусть имеется коллективный ЛПР,
- 6. При применении метода построения функции принадлежности на
- 7. В методе парных соотношений пусть имеется n
- 8. Экспертная оценка для i-го эксперта находится по
- 9. Пример построения функции принадлежности Два эксперта должны
- 10. Слайд 10
- 11. Слайд 11
- 12. Степенью нечеткого множества А называется нечеткое множество
- 13. Операция контрастной интенсификации (INT) определяется с помощью
- 14. Оператор увеличения нечеткости используется для преобразования четких
- 15. Слайд 15
- 16. Нечетким отношением R на универсальном множестве U
- 17. Пусть X = Y = (-∞;
- 18. Нечеткие отношенияНечеткое отношение R , для которого
- 19. Нечеткие отношенияПримеры1. Пусть нечеткое отношение R задано в виде:
- 20. Слайд 20
- 21. Нечеткие отношенияПусть на множестве U1×U2 заданы два
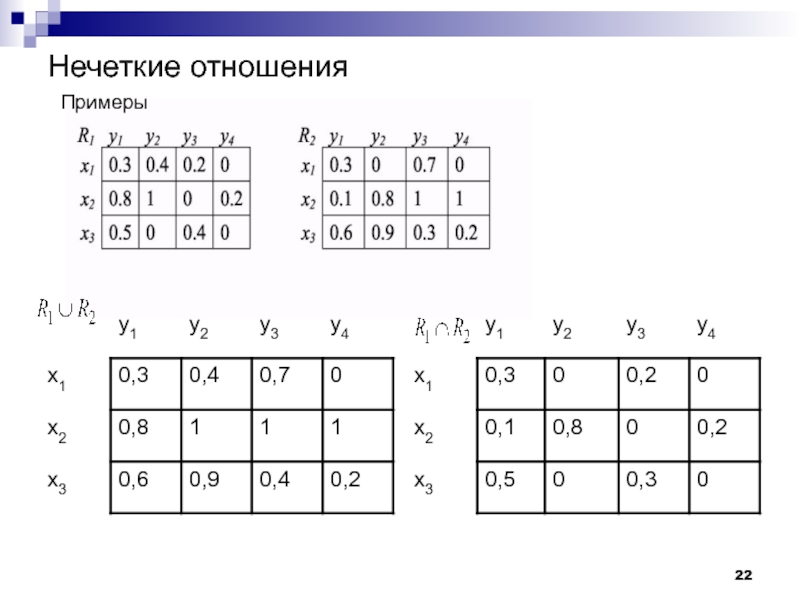
- 22. Нечеткие отношенияПримеры
- 23. Нечеткие отношенияЕсли R - нечеткое отношение с
- 24. Нечеткие отношенияВажное значение в теории нечетких множеств
- 25. Нечеткие отношенияМинимаксная композиция нечетких отношений А и
- 26. Нечеткие отношения
- 27. Поясним применение максиминной свертки на примере.Пусть R
- 28. Нечеткие отношенияПостроим соответствующее нечеткое отношение R =
- 29. Введем множество W= {1, 2, 3, 4}
- 30. Нечеткие отношенияВычислим максиминную свертку нечетких отношений R•S,
- 31. Нечеткие отношенияРассмотрим традиционный дедуктивный вывод, основанный на
- 32. Нечеткие отношенияВ среде нечетких знаний факт А
- 33. Нечеткие отношенияПоэтому если А и А* близки
- 34. Нечеткие отношенияПусть A и B— нечеткие множества,
- 35. Нечеткие отношенияПусть также задано правило A→B: «ЕСЛИ
- 36. Нечеткие отношенияВ качестве исходной посылки для вывода
- 37. Нечеткая и лингвистическая переменные Целью введения нечеткого
- 38. Нечеткая и лингвистическая переменные Лингвистической переменной (ЛП)
- 39. Нечеткая и лингвистическая переменные Примеры лингвистических переменных1. Пусть
- 40. Нечеткая и лингвистическая переменные Т- {«Малая толщина»,
- 41. Нечеткая и лингвистическая переменные Пример 2Пусть β
- 42. Нечеткая и лингвистическая переменныеВ общем случае значение
- 43. Лингвистические неопределенности Значениями лингвистической переменной являются символами
- 44. Лингвистические неопределенности Рассмотрим более простую задачу -
- 45. Лингвистические неопределенности Будем рассматривать h как оператор,
- 46. Лингвистические неопределенности В обычном использовании неопределенность очень
- 47. Лингвистические неопределенности Например, если и = маленький
- 48. Лингвистические неопределенности Порядок следования элементарных терминов в
- 49. Лингвистические неопределенности Искусственные неопределенности плюс и минус
- 50. Лингвистические неопределенности Приближенные тождества, которыми часто пользуются
- 51. Лингвистические неопределенности ПримерПусть и = маленький возраст
- 52. Лингвистические неопределенности
- 53. Лингвистические неопределенности
- 54. Скачать презентанцию
Нечеткие множестваВ работе Лотфи А. Заде «Fuzzy sets» предполагается, что функция принадлежности - это некоторое "невероятностное субъективное измерение неточности", и что она отлична от плотности вероятности и от функции распределения вероятности.
Слайды и текст этой презентации
Слайд 1Нечеткие множества
Рассмотрим более подробно физический смысл функции принадлежности. Спектр мнений
Слайд 2Нечеткие множества
В работе Лотфи А. Заде «Fuzzy sets» предполагается, что
функция принадлежности - это некоторое "невероятностное субъективное измерение неточности", и
что она отлична от плотности вероятности и от функции распределения вероятности. Иногда под функцией принадлежности понимают возможность или полезность того или иного события.
Слайд 3Нечеткие множества
Наиболее распространенным является суждение, предложенное в работе Л.А. Заде
«Понятие лингвистической переменной и его применение к принятию приближенных решений».
Согласно данному суждению под значением функции принадлежности µa(u) нечеткого множества А для любого и е U понимается вероятность того, что лицо, принимающее решение (ЛПР), отнесет элемент и к множеству А.
Слайд 4Нечеткие множества
В случае, когда А - некоторое понятие естественного языка,
a U -множество объектов, обозначаемых этим понятием A, µa(u) -
есть вероятность того, что лицо, принимающее решение, использует А в качестве имени объекта. Такая интерпретация функции принадлежности называется вероятностной и не исключает существование других интерпретаций.
Слайд 5Методы построения функции принадлежности:
Пусть имеется коллективный ЛПР, состоящий из n
экспертов. О том, что и е U принадлежит нечеткому множеству
А, n1(n1 ≤ n) экспертов отвечают положительно. В этом случаеμa(u)=n1/n
Данный метод называется частотным, а сама схема вычисления соответствует вероятностной интерпретации функции принадлежности.
Слайд 6При применении метода построения функции принадлежности на основе стандартного набора
графиков ЛПР выбирает наиболее подходящий, по его мнению, график из
стандартного набора, а затем в диалоговом режиме с ЭВМ выясняет и корректирует (при необходимости) параметры выбранного графика.
Слайд 7В методе парных соотношений пусть имеется n экспертов и необходимо
найти степени принадлежности k точек. Каждый i-ый эксперт должен определить
парные соотношения (по своему усмотрению) типа:
Слайд 8Экспертная оценка для i-го эксперта находится по формуле
Окончательно, функция
принадлежности для i-го параметра имеет вид
Слайд 9Пример построения функции принадлежности
Два эксперта должны определить насколько три
дома соответствуют оценке Пригоден для жилья. Мнение каждого из них
основывается на собственных предпочтениях. Матрица парных соотношений первого эксперта пусть имеет вид М1, а второго - М2.В матрице предпочтения М1: m11=0, т.к. оценка одного и того же дома дает равные значения, m12=1, т.к. по мнению первого эксперта первый дом более пригоден для жилья, чем второй
Слайд 12Степенью нечеткого множества А называется нечеткое множество Aα с функцией
принадлежности.
При α= 2 получаем операцию концентрирование (уплотнение)
В результате применения
этой операции к множеству А снижается степень нечеткости описания, причем для элементов с высокой степенью принадлежности это уменьшение относительно мало, а для элементов с малой степенью принадлежности относительно велико. 
Слайд 13Операция контрастной интенсификации (INT) определяется с помощью функции принадлежности следующим
образом:
Эта операция отличается от концентрирования тем, что она увеличивает значение
µA(u), которое больше 0.5 и уменьшает те, которые меньше 0.5. Таким образом, контрастная интенсификация, по существу уменьшает нечеткость А.Операции концентрирования, растяжения и контрастной интенсификации используются при работе с лингвистическими неопределенностями.
Слайд 14Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие
и для увеличения нечеткости нечеткого множества. Пусть А - нечеткое
множество, U - универсальное множество и для всех определены нечеткие множества К(и). Совокупность всех К(и) называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на нечеткое множество А является нечеткое множество
Слайд 16
Нечетким отношением R на универсальном множестве U = U1 ×
U2 называется нечеткое подмножество декартова произведения U = U1 ×
U2 , которое характеризуется такой функцией принадлежности µR(x,y), чтоПричем µR(x,y), принимается как субъективная мера выполнения отношения xRy.
Или другой способ записи:
Слайд 17
Пусть X = Y = (-∞; ∞).
Отношение х>>у
можно задать функцией принадлежности
Пусть U1={x1, x2, x3}, U2={y1,
y2, y3, y4}, М=[0,1]. Нечеткое отношение R может быть задано, к примеру, в виде таблицы: 
Слайд 18Нечеткие отношения
Нечеткое отношение R , для которого ,
при достаточно
больших k можно интерпретировать так: «х и у близкие друг
к другу числа»Носителем нечеткого отношения R на множестве U называется подмножество декартова произведения U1xU2, определяемое так:
Слайд 21Нечеткие отношения
Пусть на множестве U1×U2 заданы два нечетких отношения А
и В с функциями принадлежности μA(x,y), μB(x,y), . Тогда множество
представляет собой объединение нечетких отношений А и В на множестве U, если его функция принадлежности определяется выражениемАналогично множество является пересечением нечетких множеств A и В, если
Слайд 23Нечеткие отношения
Если R - нечеткое отношение с функцией принадлежности µR(x,y),
то отношение , характеризующееся функцией принадлежности,
называется дополнением R
на множестве X. 
Слайд 24Нечеткие отношения
Важное значение в теории нечетких множеств имеет композиция (или
произведение) нечетких отношений. В отличие от обычных (четких) отношений композицию
(произведение) нечетких отношений можно определить разными способами.Максиминная композиция (произведение) нечетких отношений А и В на U характеризуется функцией принадлежности вида
Слайд 25Нечеткие отношения
Минимаксная композиция нечетких отношений А и В на U
(обозначается A°В) определяется функцией принадлежности вида
Максимультипликативная композиция нечетких отношений
А и В на U есть нечеткое отношение А*В с функцией принадлежности вида
Слайд 27Поясним применение максиминной свертки на примере.
Пусть R — нечеткое отношение
между множествами U,V которые представляют собой совокупности натуральных чисел от
1 до 4. Семантика отношения R соответствует правилу: «ЕСЛИ и -малые числа, ТО v — большие».Определим понятия «малые числа» и «большие числа» с помощью нечетких множеств A и B соответственно:
А= 1/1 +0.6/ 2 + 0.1/3;
B = 0.1/2 + 0.6/3+1/4.
Слайд 28Нечеткие отношения
Построим соответствующее нечеткое отношение R = A•B:
Определим отношение S
из V в W. С этой целью на U определим
понятие «немалые числа», которое будет дополнением введенного ранее нечеткого множества A и обозначим его .
Слайд 29
Введем множество W= {1, 2, 3, 4} и определим на
нем понятие «очень большие числа», которое обозначим C.
C=0/1+0/2+0,5/3+1/4.
Отношение между
полными множествами U и W сформулируем в виде правила: «ЕСЛИ v - немалые числа, ТО w - очень большие числа». Построим нечеткое отношение S, соответствующее этому правилу и являющееся подмножеством декартова произведения U и W:
Слайд 30Нечеткие отношения
Вычислим максиминную свертку нечетких отношений R•S, результат которой должен
соответствовать последовательному применению двух правил: «ЕСЛИ и — малое число,
ТО v — большое»; «ЕСЛИ v - немалое число, ТО w - очень большое»:R•S=
Слайд 31Нечеткие отношения
Рассмотрим традиционный дедуктивный вывод, основанный на применении правила вывода
Modus Ponendo Ponens, в среде нечетких знаний. Вспомним его формулировку:
«ЕСЛИ А — истина, И импликация А →В - истина, ТО В — истина», т. е. из факта А и правила «ЕСЛИ А, ТО В», можно вывести B
Слайд 32Нечеткие отношения
В среде нечетких знаний факт А и образец правила
А* не обязательно всегда и везде совпадают, так как факты
представлены нечеткими множествами, являющимися подмножествами полных знаний, а правила — нечеткими отношениями, которые есть подмножества декартовых произведений полных множеств.
Слайд 33Нечеткие отношения
Поэтому если А и А* близки друг к другу,
то их можно сопоставить и получить вывод B* в сфере
их совпадения. Композиционное правило вывода в среде нечетких знаний базируется на операции максиминной свертки и имеет вид: В* = А* •R , где R — нечеткое отношение, соответствующее импликации А →В, а В* — приближенное заключение
Слайд 34Нечеткие отношения
Пусть A и B— нечеткие множества, соответствующие понятиям «малые
числа» и «большие числа» и являющиеся подмножествами полных множеств U
= V= {1, 2, 3, 4}. Функции принадлежности множеств A и B имеют вид:А= 1/1 +0.6/ 2 + 0.1/3;
B = 0.1/2 + 0.6/3+1/4.
Слайд 35Нечеткие отношения
Пусть также задано правило A→B: «ЕСЛИ и — малые
числа, ТО v - большие», формализованное нечетким отношением R
Слайд 36Нечеткие отношения
В качестве исходной посылки для вывода задан факт: «u
— число около 2», представленный нечетким множеством F функцией принадлежности
µF(u)= 0,3/1 + 1/2 + 0,3/ 3.Используя композиционное правило вывода, попробуем дать ответ на вопрос: «Что представляет собой v, если u — число около 2, и, если области U и V связаны отношением R .
G=F•R=
Слайд 37Нечеткая и лингвистическая переменные
Целью введения нечеткого множества чаще всего
является формализация нечетких понятий и отношений естественного языка (ЕЯ). Данную
формализацию можно выполнить, воспользовавшись понятиями нечеткой и лингвистической переменных.Нечеткой переменной называется совокупность (кортеж) вида
Х- наименование нечеткой переменной.
U= {и} - область ее определения (универсальное множество);
Z = - нечеткое множество на U,
описывающее ограничения на значения нечеткой переменной X.
Слайд 38Нечеткая и лингвистическая переменные
Лингвистической переменной (ЛП) называется кортеж вида
, где
β - наименование лингвистической
переменнойТ - множество ее значений (терм-множество), представляющих собой наименование нечетких переменных, областью определения каждой из которых является множество U. Множество Т называется базовым терм-множеством лингвистической переменной
G - синтаксическая процедура, описывающая процесс образования из элементов множества Т новых, осмысленных для данной задачи значений лингвистической переменной (терм).
М - семантическая процедура, позволяющая превратить каждое новое значение ЛП, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.
Слайд 39Нечеткая и лингвистическая переменные
Примеры лингвистических переменных
1. Пусть эксперт определяет толщину
выпускаемого изделия с помощью понятий «Малая толщина», «Средняя толщина» и «Большая
толщина», при этом минимальная толщина равна 10 мм, а максимальная - 80 мм.Формализация такого описания может быть проведена с помощью следующей ЛП < β, Т, U, G, М>, где
β- толщина изделия;
Слайд 40Нечеткая и лингвистическая переменные
Т- {«Малая толщина», «Средняя толщина», «Большая
толщина»};
U=[10,80];
G - синтаксическая процедура образования новых термов с помощью связок
«и», «или», и модификаторов (лингвистических неопределенностей) типа «очень», «не», «слегка» и т.п. Например, «Малая или средняя толщина», «Очень малая толщина», «Не очень большая толщина» и т.д.М - семантическая процедура задания на U= [10,80] нечетких множеств A1=«Mалая толщина», А2=«Средняя толщина», А3=«Большая толщина», а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок, лингвистических неопределенностей и других операций над нечеткими множествами.
![Нечеткая и лингвистическая переменные Т- {«Малая толщина», «Средняя толщина», «Большая толщина»};U=[10,80];G - синтаксическая процедура образования новых термов](/img/thumbs/e17d71e41c5487ec478d128757d5a5d6-800x.jpg "Нечеткие множества Нечеткая и лингвистическая переменные Т- {«Малая толщина», «Средняя толщина», «Большая толщина»};U=[10,80];G")
Слайд 41Нечеткая и лингвистическая переменные
Пример 2
Пусть β - посадочная скорость
самолета (скорость). Тогда Скорость := (скорость, , [0..300],G,
M), гдеG - процедура перебора элементов базового терм-множества.
М-процедура экспертного опроса.
Слайд 42Нечеткая и лингвистическая переменные
В общем случае значение лингвистической переменной есть
составной термин, представляющий сочетание некоторых элементарных терминов. Эти элементарные термины
можно разбить на четыре основные категории:первичные термины, которые являются символами специальных нечетких подмножеств, например, молодой, старый и т.д.
отрицание НЕ и союзы И, ИЛИ.
неопределенности типа: очень, слабо, более или менее и т.д.
маркеры, чаще всего это вводные слова.
Отрицание НЕ, союзы И, ИЛИ, неопределенности типа очень, весьма, больше, меньше и другие термины, которые входят в определение значений лингвистической переменной, могут рассматриваться как символы различных операций, определенных на нечетких подмножествах U.
Слайд 43Лингвистические неопределенности
Значениями лингвистической переменной являются символами нечетких подмножеств, которые
представляют собой фразы или предложения формального или естественного языка.
Например, если
U есть набор целых чисел U= (0, 1, 2,. .., 100) и возраст есть лингвистическая переменная, тогда значения лингвистической переменной могут определяться словосочетаниями: молодой, не молодой, очень молодой, не очень молодой, старый и т.д.Основная проблема, которая возникает при использовании лингвистической переменной, заключается в следующем: пусть дано значение любого элементарного термина хi, i = 1..n, в составном термине u = x1...xn, который представляет собой значение лингвистической переменной. Требуется вычислить значение и в смысле нечеткого множества.
Слайд 44Лингвистические неопределенности
Рассмотрим более простую задачу - вычисление значения составного
термина вида и = hx, где h - неопределенность, a
x - термин с фиксированным значением. Например, и = очень высокий человек, где h = очень, a x = высокий человек.
Слайд 45Лингвистические неопределенности
Будем рассматривать h как оператор, который переводит нечеткое
множество М(х), представляющее значение x, в нечеткое M(hx). Теперь неопределенность
выполняет функцию генерации большого множества значений для лингвистической переменной из небольшого набора первичных элементов.Например, используя неопределенность очень в сочетании с отрицанием НЕ и первичным термином высокий, мы можем генерировать нечеткие множества очень высокий, не очень высокий и т.п.
Слайд 46Лингвистические неопределенности
В обычном использовании неопределенность очень не имеет четко
определенного значения. Она действует как усилитель, генерируя подмножества того множества,
к которому она применяется. Аналогичным образом действует операция концентрирования. Поэтому очень и, где и - некоторый термин, может быть определенно как и2, т.е.
Слайд 47Лингвистические неопределенности
Например, если и = маленький возраст = (1/1,
0.8/2, 0.6/3, 0.4/4, 0.2/5), тогда
очень маленький = (1/1, 0.64/2, 0.36/3,
0.16/4, 0.04/5).Рассматриваемый как оператор, очень может сочетаться с самим собой. Так, например:
очень очень маленький = (1/1, 0.4/2, 0.1/3)
Слайд 48Лингвистические неопределенности
Порядок следования элементарных терминов в составном термине существенно
влияет на результат. Так, например:
не одно и то же.
Слайд 49Лингвистические неопределенности
Искусственные неопределенности плюс и минус служат для придания
более слабых степеней концентрации и растяжения, чем те, которые определяются
операциями CON и DIV.
Слайд 50Лингвистические неопределенности
Приближенные тождества, которыми часто пользуются на практике:
плюс и
= минус очень и
минус очень очень и = плюс плюс
очень и 
Слайд 51Лингвистические неопределенности
Пример
Пусть и = маленький возраст = (1/1, 0.8/2,
0.6/3, 0.4/4, 0.2/5). Определим лингвистическую переменную не очень
очень маленький возраст.
