Неэмпирическая квантовая химия

квантовой химии
Москва 2007 г.
Лекция 6. Неэмпирическая квантовая химия. Базисные функции

для расчетов в приближении MO ЛКАО.
.

Цирельсон В.Г. , Бобров М.Ф. «Квантовая химия молекул».

химия
квантовая
статистическая
механика
молекулярная
механика




Методы вычислительной химия наноразмерных систем

молекулы, число электронов и базис, в котором будет произведен расчет.

Базисные функции для расчетов в приближении MO ЛКАО
 Использование аналитических (базисных) АО упрощает вычисления. Угловые части АО - угловые гармоники. Рассмотрим аналитические приближения к радиальным частям AO.
  Орбитали слейтеровского типа (STO или ОСТ) - приближения к радиальным составляющим точных водородоподобных AO. ОСТ отвечают потенциалу центрального поля
V( r ) = - n/r + [n(n-1) – l(l+1)]/2r2
и удовлетворяют асимптотическому поведению как вблизи ядра, так и на больших расстояниях от него. При l = -1 ОСТ переходит в АО водородоподобного атома с = Z/n.
В сферических координатах ОСТ имеют вид:


N - нормировочный множитель, - орбитальная экспонента,
- сферическая гармоника, n, l, и m - квантовые числа.
-ОСТ с l>1 - безузловые;
-ОСТ с одинаковыми l, но разными n, неортогональны.

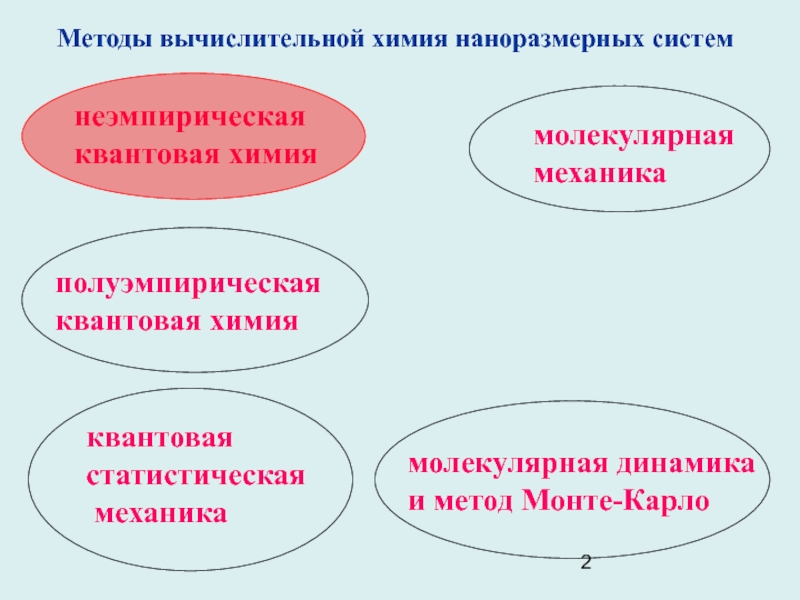
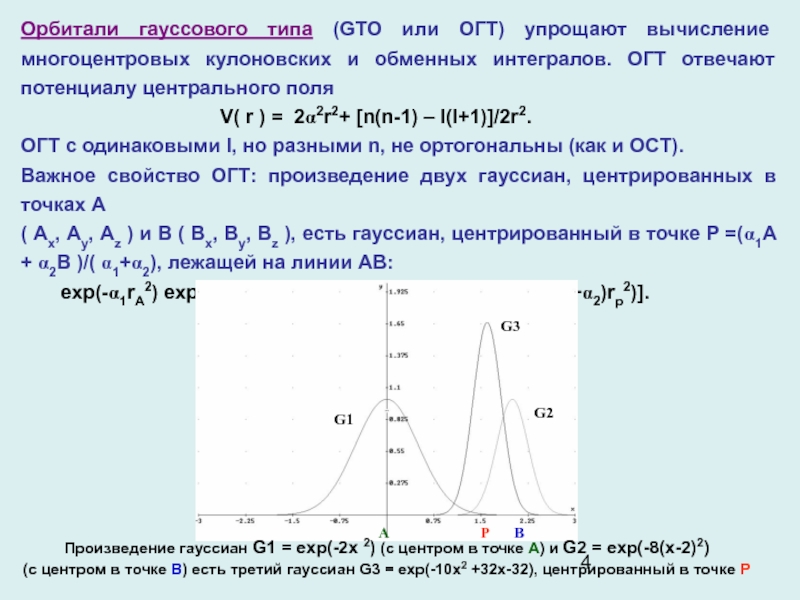
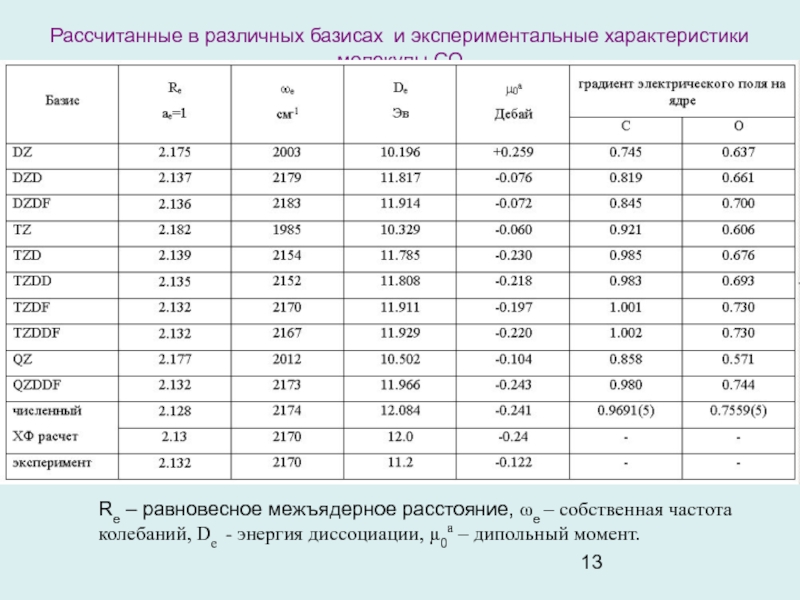
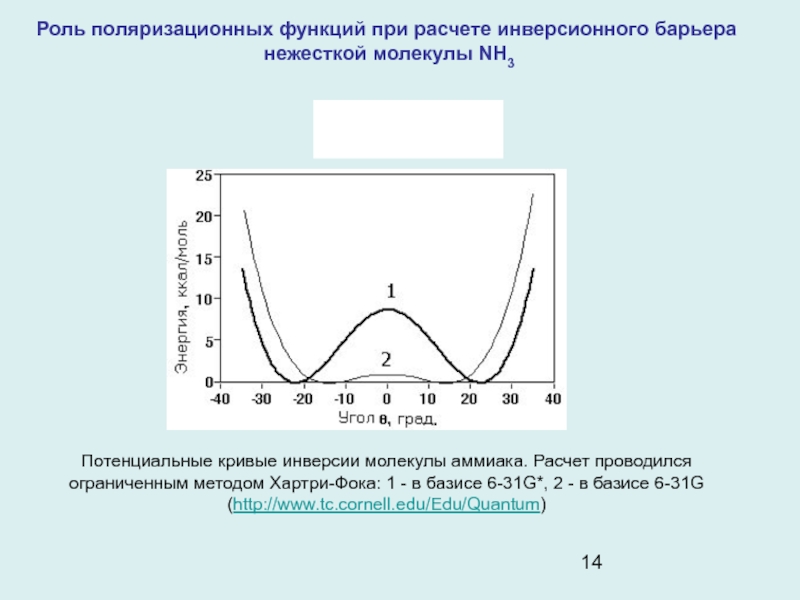
и обменных интегралов. ОГТ отвечают потенциалу центрального поля
V( r )

= 2α2r2+ [n(n-1) – l(l+1)]/2r2.
ОГТ с одинаковыми l, но разными n, не ортогональны (как и ОСТ).
Важное свойство ОГТ: произведение двух гауссиан, центрированных в точках А
( Аx, Аy, Аz ) и В ( Вx, Вy, Вz ), есть гауссиан, центрированный в точке P =(α1A + α2B )/( α1+α2), лежащей на линии АВ:
exp(-α1rA2) exp(-α2rB2)= exp[-(α1α2rAB2)/( α1+α2)] exp[(-α1+α2)rp2)].

Произведение гауссиан G1 = exp(-2x 2) (с центром в точке А) и G2 = exp(-8(x-2)2)
(с центром в точке В) есть третий гауссиан G3 = exp(-10x2 +32x-32), центрированный в точке Р

G3

G1

G2

А

B

P

коэффициентами. Поэтому в квантово-химических расчетах используются, как правило, базисные наборы

из ОГT.
 Декартовы ОГT в координатах x, y, и z имеют вид
, r2= x2 + y2 + z2.
n, l, и m определяют угловую часть функции в декартовых координатах. Сумма (l+м+n) аналогична угловому квантовому числу для атомов и используется, чтобы обозначать функции s-типа (l=0), p-типа (l=1), d-типа (l=2), f-типа (l=3), и т.д.



 



Декартовы ОГT называют гауссовыми примитивами. Это - не орбитали, а простые и удобные математические функции. Недостаток ОГT - их поведение вблизи и вдали от ядра отличается от поведения водородоподобных АО.

всего описывать ОСТ. Сейчас базисные наборы непосредственно строят из линейных

комбинаций ОГT и из сгруппированных (контрактированных) ОГT (CGTO или СОГТ): g = ∑аiGi.
«Группировка» (контрактация, сжатие) означает, что функция gj используется как базисная функция, т.е. χ= ∑сjgj. Каждая СОГТ имеет свои собственные фиксированные коэффициенты аi и экспоненциальные множители в примитивах Gi.
Контрактация уменьшает время вычисления интегралов в методе Рутана, зависящее от 4-ой степени числа базисных функций.
Номенклатура базисных наборов
1) Структура базисного набора может быть определена для АО отдельных атомов (Фудзинага, Даннинг): СОГТ получают, аппроксимируя одну ОСТ с ξ=1.0. Затем экспоненты в ОГТ умножают на ξ2 из ОСТ. ξ подбирают оптимальным для данной молекулы.
Такие базисы обозначают STO-nG (n-число примитивов в СОГТ). Экспоненты гауссиан для базисных функций, описывающих орбитали с тем же самым основным квантовым числом (например, для 2s и 2p функций), берутся одинаковыми.

только одна функция на пару электронов остова и одна функцию

на каждую валентную АО в основном состоянии. Учитываются все АО частично занятых подоболочек т.е. валентные АО s- и p-типа для элементов первых 2 групп периодической системы: 1s, 2s, 2px, 2py, 2pz . Так, для атомов Li и Be имеется 2 СОГТ s-типа и 1 СОГТ p-типа (Ве). Минимальный базисный набор для S атома имеет 3 СОГТ s-типа и 2 СОГТ p-типа.
Минимальный базисный набор называют также одноэкпоненциальным или единичным зета набором (SZ, где Z означает экспоненциальный множитель).

Расширенный базисный набор - используя две, три и т.д. функций на одну орбиталь: можно добиться лучшего описания МО. Соответственно, различают двух- (дубль-зета -DZ), трехэкспоненциальный (TZ) и т.д. базисы.
Валентно-расщепленный (SV) базисный набор. При образовании химической связи валентные АО более подвержены воздействию других атомов, чем внутренние (остовные) орбитали. Поэтому для их описания требуются большее количество базисных функций (число примитивов может оставаться тем же).

из атомных ХФ расчетов, дополняют другими функциями. Поляризационные функции имеют

более высокие значения l чем в занятой АО соответствующего атома. Экспоненты для них определяют в расчетах молекул (т.к. в атомах соответствующие АО не заняты электронами).
Диффузные функции важны для правильного описания анионов и слабых связей (например водородных связей), для вычислений дипольного момента, поляризуемости, и т.д. Это гауссианы с очень маленькими экспонентами, медленно спадающие с расстоянием от ядра. Диффузный гауссиан имеет обычно s- и p-тип.
 
"Зета" терминология применяется и для поляризационных функций. Так, DZP означает двухэкпоненциальный базис плюс поляризационные функции, TZP – трехэкпоненциальный базис плюс поляризация, и т.д. Иногда число поляризационных функций обозначается как TZDP или TZ2P, TZ + 2P: тройной зета базис плюс двойная поляризация.

молекулы, а не для отдельных атомов и обозначается n-ijG или

n-ijkG:
n - число примитивов для внутренних оболочек;
ij (DZ наборы) или ijk (TZ наборы)- число примитивов для СОГТ валентных оболочек.
Число примитивов s-типа и p-типа для одной и той же электронной оболочки одинаково, они имеют одинаковые экспоненты, но коэффициенты для s- и p-типа сжатий различны.

Базисные наборы Попла могут также быть расширены за счет включения поляризационных функций (d-типа для неводородных атомов и p-типа для атомов водорода) и диффузных функций (по 1 диффузному гауссиану s- и p-типа с одинаковыми экспонентами для тяжелых атомов и 1 диффузного гауссиана s-типа для водорода).

Z ≤ 9

и плотностями составляющих ее атомов), вычисленные с использованием следующих базисных

наборов:
.SZ;
.DZ;
.TZ;
.DZ+DP;
.TZ+DP;
.TZ+2DP;
.TZ+DP+FP;
.TZ+2DP+2FP.

равновесное межъядерное расстояние, ωe – собственная частота колебаний, De -

энергия диссоциации, μ0a – дипольный момент.

кривые инверсии молекулы аммиака. Расчет проводился ограниченным методом Хартри-Фока: 1

- в базисе 6-31G*, 2 - в базисе 6-31G (http://www.tc.cornell.edu/Edu/Quantum)

к электрону точности, соответствующей расчету в базисе 6–311+G**(2df) с оптимизацией

геометрии и учетом по теории возмущений всех одно–, двух–, трех– и четырехкратно возбужденных конфигураций. В основе этих схем лежит замеченная аддитивность энергии:
Е[ MP3/6–31G**] ≈ E[MP3/6–31G] + {E[HF/6–31G**] – E[HF/6–31G]}.
Геометрия (и частоты) в этих схемах оптимизируются на уровне расчета MP2/6–31G*, а затем при фиксированной геометрии проводят расчеты с учетом возбужденных конфигураций высших порядков.

Поплом с сотр. предложили схемы, известные как Gaussian–1 (G1) и Gaussian–2 (G2). В схеме G1 при расчете корреляционной энергии используется базис 6–311G**(2df, p):

В схеме G2 корреляционная энергия определяется в базисе 6–311+G(3df, 2p).
В итоге удается достичь точности расчета энергии атомизации ~ 4 кДж/моль, а теплоты образования ~ 10 кДж/моль.