НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТЕМАТИКИ

точками содержит отрезок, соединяющий эти точки.

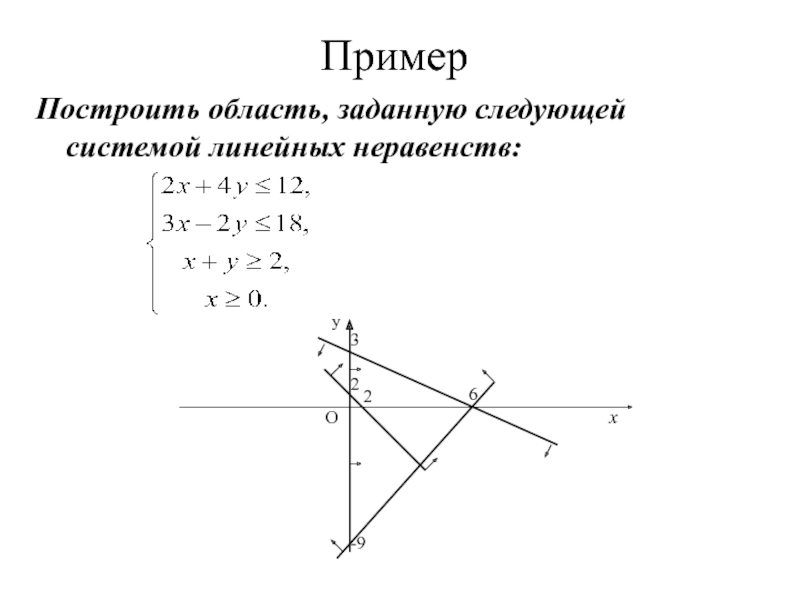
выпуклое множество невыпуклое множество
Выпуклый многоугольник расположен по одну сторону от каждой из прямых - его границ.
Выпуклой линейной комбинацией точек М1, М2, ...,Мn называется любая точка М такая, что:
М=a1M1+a2M2 + ... +anMn,
где ai > 0 и a1+a2+ ... +an=1.

содержит и выпуклую произвольную комбинацию этих точек.
Поскольку произвольная

точка отрезка представляет собой выпуклую комбинацию его концов, то это и означает, что выпуклое множество вместе с двумя данными точками содержит весь соединяющий их отрезок.
Всякая точка выпуклого многоугольника, лежащая внутри его или на одной из сторон, за исключением вершин, может быть представлена как выпуклая линейная комбинация других точек этого многоугольника. Вершины многоугольника не представляются в виде выпуклой комбинации двух каких-нибудь других точек. В этом смысле вершины многоугольника являются экстремальными точками.

по крайней мере, одну общую точку и весь многоугольник расположен

по одну сторону от этой прямой.
Через каждую из вершин многоугольника можно провести бесконечное множество опорных линий.
Опорной называется всякая плоскость, имеющая с выпуклым многогранником, по крайней мере, одну общую точку, причем, весь многогранник расположен по одну сторону от нее.
Опорная плоскость может иметь с выпуклым многогранником общую точку (его вершину), общую прямую (ребро), или общую грань.

вида
ai1x1+ai2x2 < bi ,

i =1,2,3,…,n,
каждое из которых определяет в R 2 некоторую полуплоскость, которой принадлежит и сама граничная прямая ai1x1+ai2x2 = bi .
Выпуклый многогранник в R 3 можно задать аналитически, с помощью системы линейных неравенств вида
ai1x1+ai2x2+ai3x3 < bi , i =1,2,3,…,n,
каждое из которых определяет полупространство, которому принадлежит и сама граничная плоскость ai1x1+ai2x2+ai3x3 = bi .

из m-линейных неравенств (или уравнений) с n переменными х1, х2,

..., хn , определяющая некоторое выпуклое множество в n-мерном пространстве Rn, ограниченное или бесконечное.
Допустим также, что задана некоторая линейная форма от этих переменных, определяющая целевую функцию:
f (х)= c1x1 + c2x2 + ... + cn xn .
В каждой точке выпуклого множества, т.е. для каждого решения системы х = (х1, х2, ..., хn), линейная функция f (х) принимает определенное значение.
Вопрос: в каких точках выпуклого множества линейная функция f (х) достигает своего наибольшего и наименьшего значения, если они существуют?
Решение этой задачи сводится к отысканию точек выпуклого множества, в которых заданная линейная функция достигает экстремального значения.

значения в одной из вершин выпуклого многогранника (они являются

её точками экстремума).