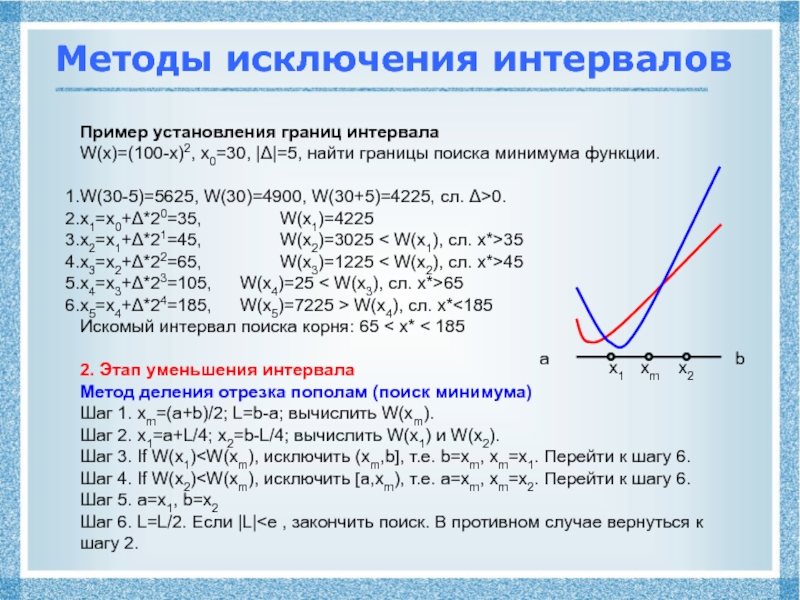
поиска минимума функции.
W(30-5)=5625, W(30)=4900, W(30+5)=4225, сл. >0.
x1=x0+*20=35, W(x1)=4225
x2=x1+*21=45, W(x2)=3025 < W(x1), сл.
x*>35
x3=x2+*22=65, W(x3)=1225 < W(x2), сл. x*>45
x4=x3+*23=105, W(x4)=25 < W(x3), сл. x*>65
x5=x4+*24=185, W(x5)=7225 > W(x4), сл. x*<185
Искомый интервал поиска корня: 65 < x* < 185
2. Этап уменьшения интервала
Метод деления отрезка пополам (поиск минимума)
Шаг 1. xm=(a+b)/2; L=b-a; вычислить W(xm).
Шаг 2. x1=a+L/4; x2=b-L/4; вычислить W(x1) и W(x2).
Шаг 3. If W(x1)
Шаг 4. If W(x2)Шаг 5. a=x1, b=x2
Шаг 6. L=L/2. Если |L|а
b
x1
x2
xm



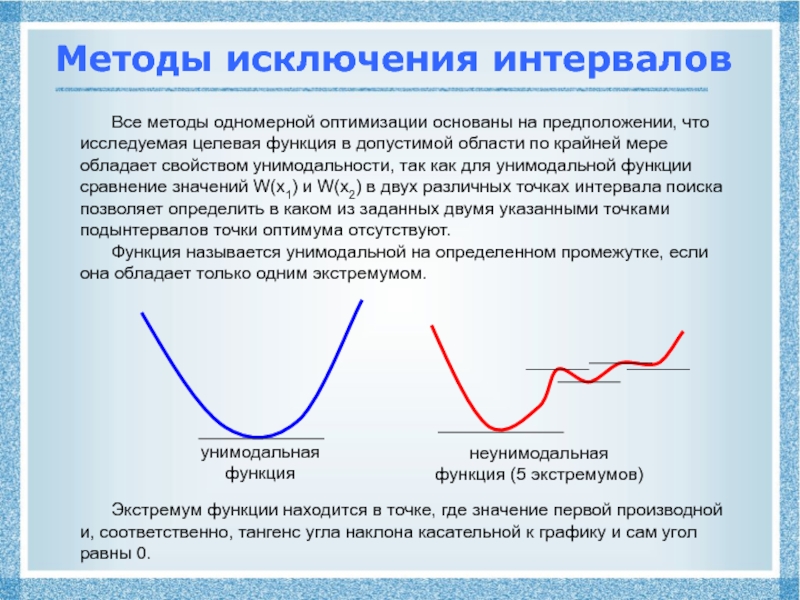
![Нелинейное программирование
Задачами нелинейного программирования (НЛП) Методы исключения интерваловПравило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], Методы исключения интерваловПравило исключения интервалов Пусть W(x) унимодальна на отрезке [a,b], а ее минимум достигается в точке](/img/thumbs/5539f7f98c2bcc86dce04c81754e91d3-800x.jpg)

![Нелинейное программирование
Задачами нелинейного программирования (НЛП) Методы исключения интерваловМетод золотого сеченияПоиск минимума на участке [a,b].Шаг 1. x1=a+(1-K)(b-a).Шаг Методы исключения интерваловМетод золотого сеченияПоиск минимума на участке [a,b].Шаг 1. x1=a+(1-K)(b-a).Шаг 2. x2=a+K(b-a).Шаг 3. If |x1 -](/img/thumbs/b9861a0adb7b1264857bf27bb1504b06-800x.jpg)
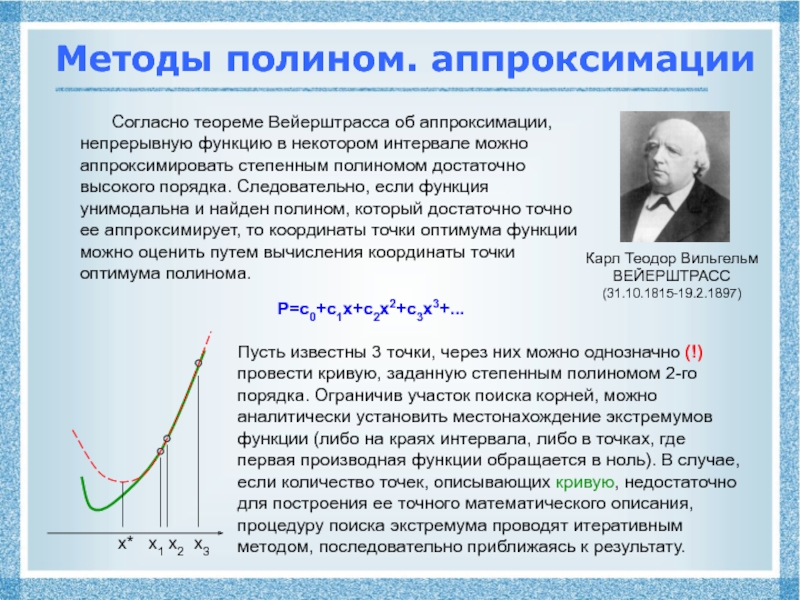


![Нелинейное программирование
Задачами нелинейного программирования (НЛП) Методы с исполь-ем производныхМетод хордОриентирован на нахождение корня уравнения W'(x) в Методы с исполь-ем производныхМетод хордОриентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две](/img/thumbs/18feab6daa49df91ada8420f1b01fa0e-800x.jpg)
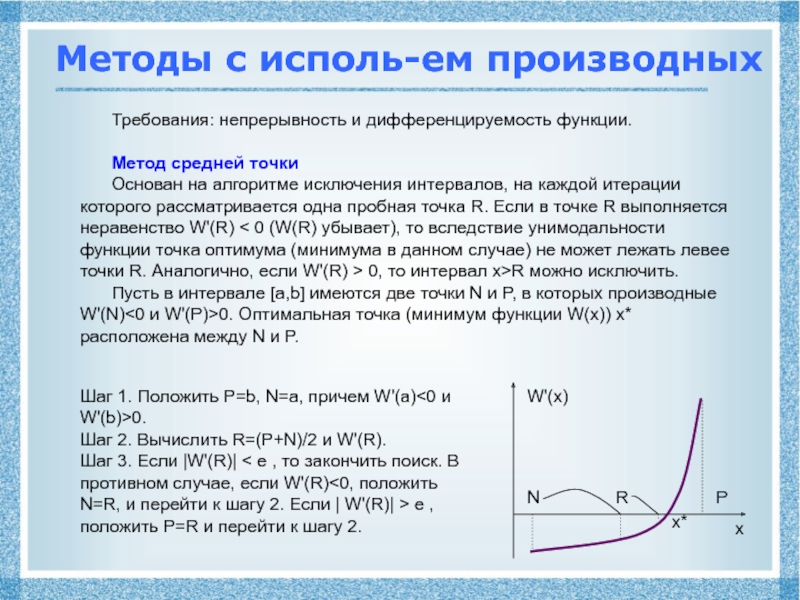
![Нелинейное программирование
Задачами нелинейного программирования (НЛП) Методы с исполь-ем производныхМетод касательныхОриентирован на нахождение корня уравнения W'(x) в Методы с исполь-ем производныхМетод касательныхОриентирован на нахождение корня уравнения W'(x) в интервале [a,b], в котором имеются две](/img/thumbs/34614e062fe4671e5b4eefb7ce4ca019-800x.jpg)



















