Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Необходимое условие существования определенного интеграла 2. СВОЙСТВА
Содержание
- 1. Необходимое условие существования определенного интеграла 2. СВОЙСТВА
- 2. Достаточное условие существованияопределенного интегралаЕсли на отрезке [a,b]
- 3. Свойстваопределенного интеграла1Постоянный множитель можно выноситьза знак определенного интеграла.
- 4. Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор
- 5. Следовательно по определению:
- 6. 2Определенный интеграл от алгебраической суммы (разности) двух функций равен сумме (разности) интегралов от этих функций.
- 7. 3Если отрезок интегрирования разбит на части, то
- 8. Геометрически это означает, что если a
- 9. SSS
- 10. 4Если на [a,b], где a
- 11. Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор
- 12. Следствие.Пусть на [a,b], где a
- 13. Доказательство:По свойству 4 имеем:По свойству 1 и геометрическому смыслу определенного интеграла:
- 14. 5Если на [a,b], где a
- 15. Доказательство:По свойству функции, непрерывной на отрезке, для
- 16. Но функция, непрерывная на отрезке, принимает любое
- 17. ПустьТогда теорема о среднем утверждает, что найдется
- 18. Слайд 18
- 19. Равенствоназывается формулой среднего значения.называется средним значением функции.
- 20. 6Если на [a,b] функция y=f(x) неотрицательна, то
- 21. Скачать презентанцию
Достаточное условие существованияопределенного интегралаЕсли на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на этом отрезке.
![Презентация на тему Необходимое условие существованияопределенного интеграла2. СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛАИнтегрируемая на отрезке Необходимое условие существованияопределенного интеграла2. СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛАИнтегрируемая на отрезке [a,b] функция y=f(x) ограничена на этом отрезке.](/img/thumbs/a07599203f59857581c4900be469a5ca-800x.jpg)
![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА Достаточное условие существованияопределенного интегралаЕсли на отрезке [a,b] функция y=f(x) непрерывна, то Достаточное условие существованияопределенного интегралаЕсли на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на этом отрезке.](/img/thumbs/1450bebcb26bd2123186909bda5db8a2-800x.jpg)

![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму:Переходим Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму:Переходим к пределу в левой и правой](/img/thumbs/0ca5f0c2ae0a93daca8b648129f6aa33-800x.jpg)




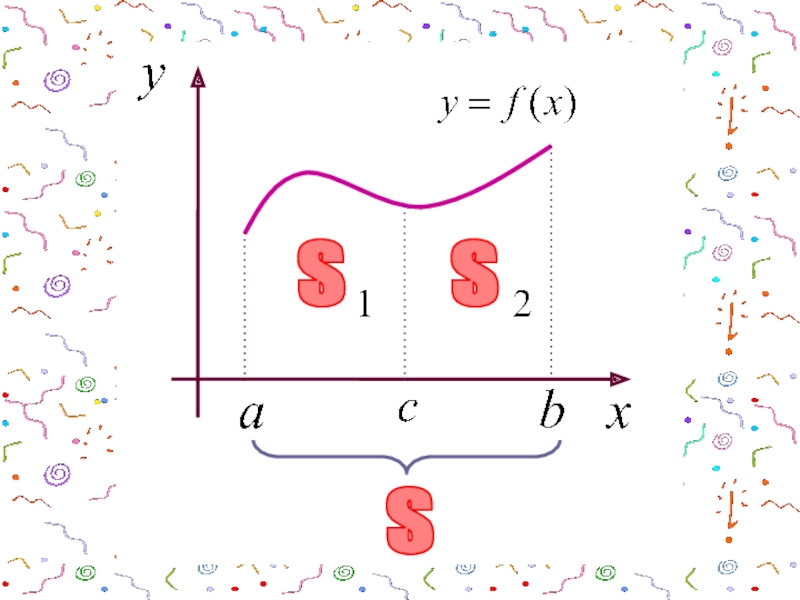
![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА 4Если на [a,b], где a 4Если на [a,b], где a](/img/thumbs/a6c3a6851e14d60782a6e118740b8acf-800x.jpg)
![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных Доказательство:Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных сумм:ЕслиПереходим к пределу в левой и](/img/thumbs/3c008e18b7c3d51ddca2b7b957acbfd4-800x.jpg)
![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА Следствие.Пусть на [a,b], где a Следствие.Пусть на [a,b], где a](/img/thumbs/f76a784f976174b024de975619710d1e-800x.jpg)

![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА 5Если на [a,b], где a 5Если на [a,b], где a](/img/thumbs/bf01bc4d4c954975770ed05700a38d93-800x.jpg)


![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА ПустьТогда теорема о среднем утверждает, что найдется такая точкачто площадь под ПустьТогда теорема о среднем утверждает, что найдется такая точкачто площадь под кривой y=f(x) на [a,b] равна площади](/img/thumbs/ac624cdcb7678deeca8eefb0dd2feddb-800x.jpg)
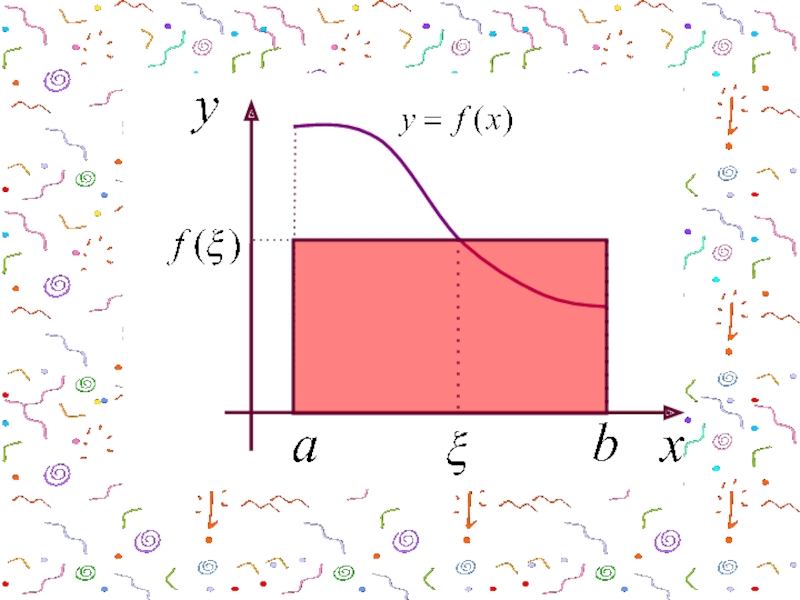

![Необходимое условие существования
определенного интеграла
2. СВОЙСТВА 6Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой 6Если на [a,b] функция y=f(x) неотрицательна, то площадь под этой кривой численно равна определенному интегралуГеометрический смыслопределенного интеграла](/img/thumbs/0f748ff8672aae066f80b65afcf3f249-800x.jpg)



















