Необыкновенная девочка

по 100 книг носила
Всё это правда,
А не бред
Когда пыля 10

ног,
Она бежала по дороге
За ней всегда бежал щенок
С одним хвостом
Зато 100 – ногий.
И 10 удивлённых глаз
Смотрели в этот мир привычно
Но станет всё совсем обычно
Когда поймете наш рассказ!

числа
двоичная система счисления
восьмеричная система счисления
шестнадцатеричная система счисления

правила записи чисел.
Цифры - знаки, при помощи которых записываются

числа.
Алфавит системы счисления - совокупность цифр.

Общие сведения

Древнеславянская система счисления

Вавилонская система счисления

Египетская система счисления

результате каких-либо операций из узловых чисел.
 100 +
 10

+

=

ней для записи любых чисел используется всего один символ -

палочка, узелок, зарубка, камушек.

Унарная система счисления

Узелковое письмо «кипу»

Зарубки

Примеры узлов «кипу»

Узелки, дощечки

Камушки

эквивалент (количественное значение) цифры в числе не зависит от её

положения в записи числа.

Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

зависит от её положения в записи числа.
Основание позиционной системы счисления

равно количеству цифр, составляющих её алфавит.

Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Позиционная система счисления

стали пользоваться подобной нумерацией около 800 г. н. э.
Примерно в

1200 г. н. э. эту нумерацию начали применять в Европе.

Десятичная система счисления

быть представлено в виде:
Aq =±(an–1qn–1+ an–2  qn–2+…+ a0 

q0+ a–1q–1+…+ a–m q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.

Основная формула

473, 5810 = 4 * 100 + 7 * 10 + 3 * 1 =
4 * 102 + 7 * 101 + 3 * 100+5*10-1 + 8*10-2

a–1  q–1+…+ a–m  q–m)

Примеры записи чисел в

развёрнутой форме:

201210=2103 +0102 +1101 +2100

0,12510=110-1 +210-2 +510–3

14351,110=1104 +4103 +3102 +5101 +1100 +110–1

Развёрнутая форма

+ 2 * 100 + 3*10-1 + 5*10-2
=5 * 102

+ 3 * 101 + 7*100 +9*10-1 + 4*10-2

по 0,5 балла

основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно

записать:
an–1an–2…a1a0 = an–12n–1 + an–22n–2 +…+ a020
Например:

100112 =124+023+022+121+120 = 24 +21 + 20 =1910

Правило перевода двоичных чисел в десятичную систему счисления:

Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа

+ 1*22 + 1*21 + 1*20
=1*23 + 0*22 + 1*21

+ 0*20

=7*83 + 0*82 + 2*81 + 5*80 + 3*10-1

По 0,5 балла

0
разряды
= 1·22 + 0·21 + 1·20
= 4 + 0 +

1 = 510

Правило перевода целых десятичных чисел в двоичную систему счисления

в десятичную систему счисления следует перейти к его развёрнутой записи

и вычислить значение получившегося выражения.

Восьмеричная система счисления

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.

Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.

6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная

система счисления

Переведём десятичное число 154 в шестнадцатеричную систему счисления:

15410 = 9А16

154

16

9

-144

10

(А)

9

16

0

3АF16 =3162+10161+15160 =768+160+15=94310.

на основание новой системы счисления до тех пор, пока не

получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.

Цифровые весы

Правило перевода целых десятичных чисел в систему счисления с основанием q

до 16

сложения и умножения:
Арифметика одноразрядных двоичных чисел
Арифметика многоразрядных двоичных чисел
Умножение и

деление двоичных чисел

числа представляются в компьютере с помощью простых технических элементов с

двумя устойчивыми состояниями;
представление информации посредством только двух состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий логические преобразования двоичных данных.

Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.

правила записи чисел.
Система счисления называется позиционной, если количественный эквивалент

цифры в числе зависит от её положения в записи числа.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq =±(an–1qn–1 + an–2qn–2 +…+ a0q0 + a–1q–1 +…+ a–mq–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.

Самое главное

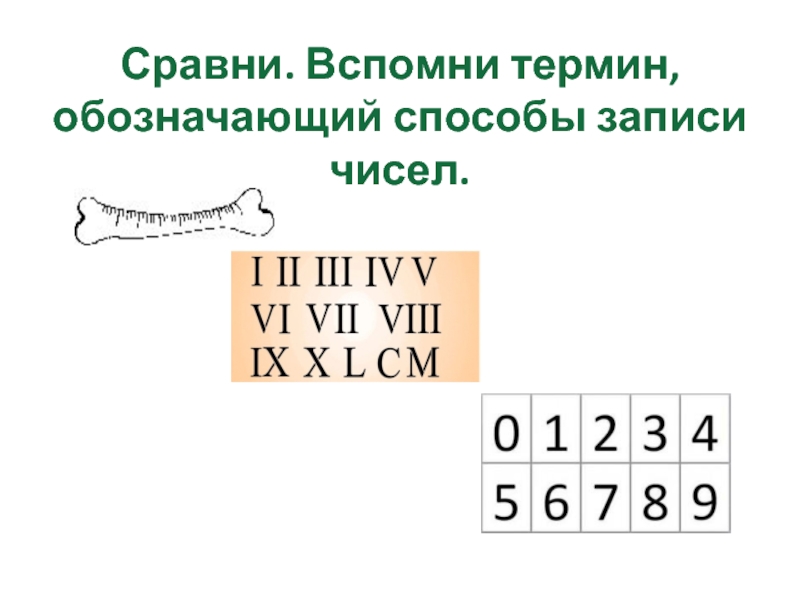
Цифры каких систем счисления приведены на рисунке?
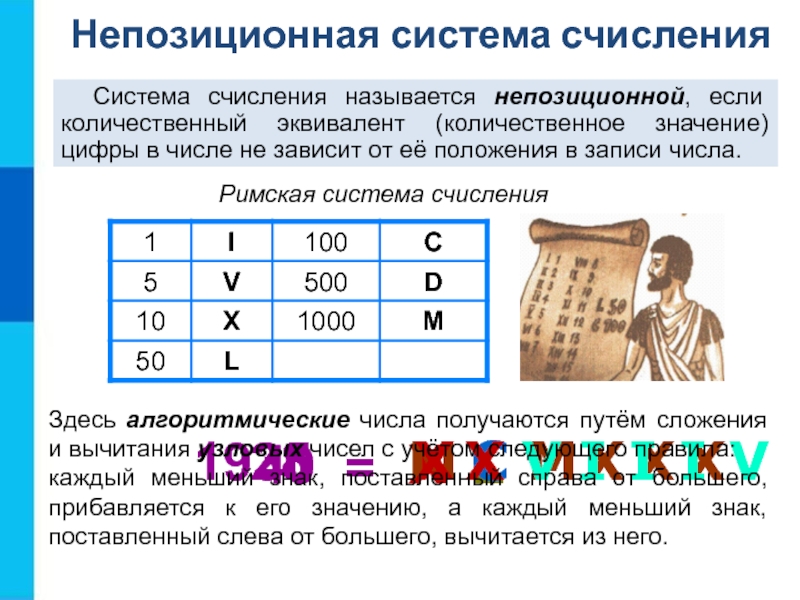
Объясните, почему позиционные

системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.

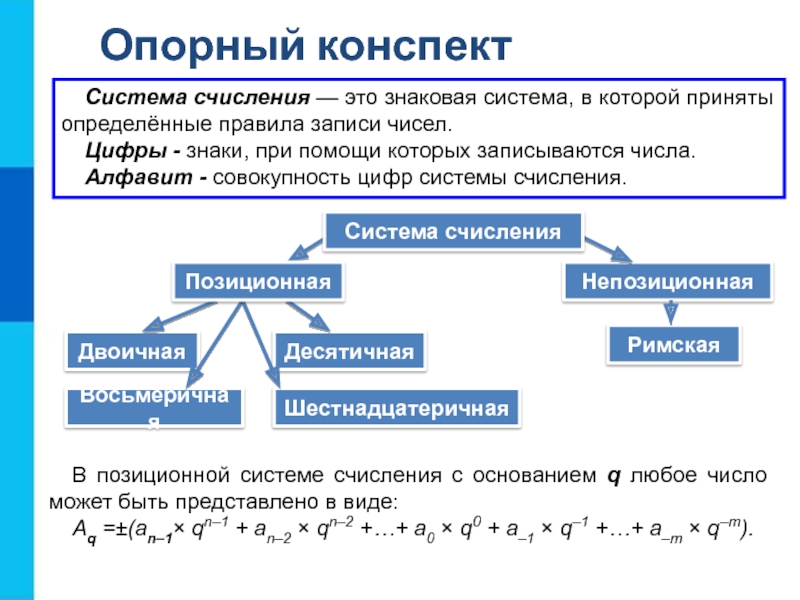
Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?

Запишите в развёрнутом виде числа:
а) 143,51110
б) 1435118
в) 14351116
г) 1435,118

Запишите десятичные эквиваленты следующих чисел:
а) 1728
б) 2ЕА16
в) 1010102
г) 10,12
д) 2436

Укажите, какое из чисел 1100112, 1114,358 и1В16 является:
а) наибольшим
б) наименьшим

Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.

Верны ли следующие равенства?
а) 334 =217
б) 338 =214

Найдите основание х системы счисления, если:
а) 14x=910
б) 2002x=13010

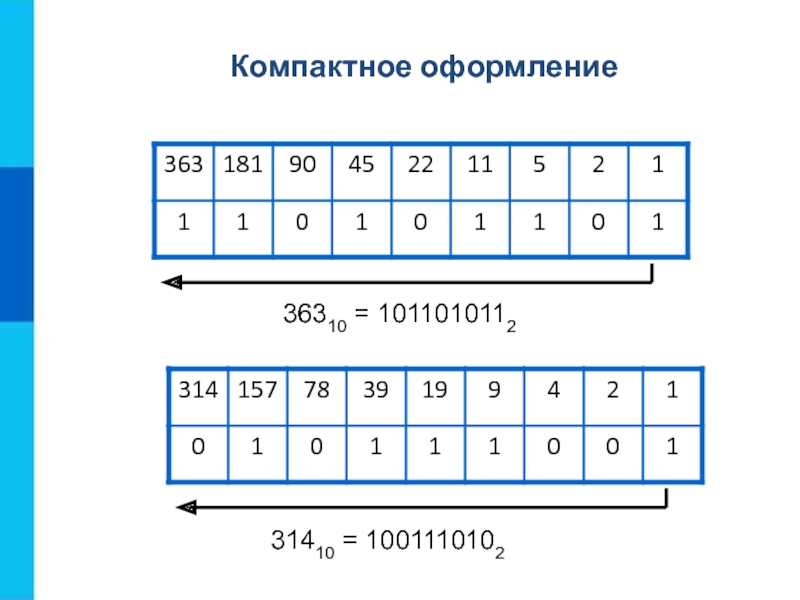
Переведите целые числа из десятичной системы счисления в двоичную:
а) 89
б) 600
в) 2010

Переведите целые числа из десятичной системы счисления в восьмеричную:
а) 513
б) 600
в) 2010

Переведите целые числа из десятичной системы счисления в шестнадцатеричную:
а) 513
б) 600
в) 2010

Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.

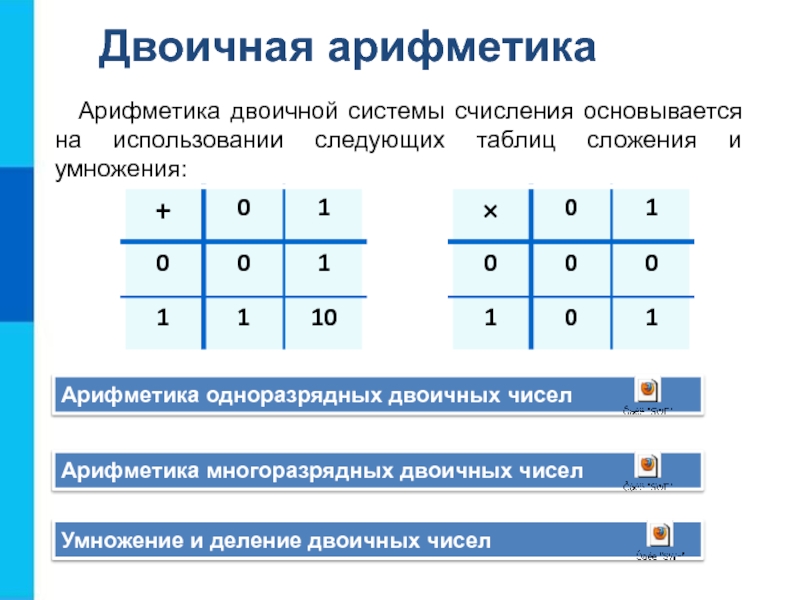
Выполните операцию сложения над двоичными числами:
а) 101010 + 1101
б) 1010 + 1010
в) 10101 + 111

Выполните операцию умножения над двоичными числами:
а) 1010 · 11
б) 111 · 101
в) 1010 · 111

Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:
а) 1100 ? 11 ? 100 = 100000;
б) 1100 ? 10 ? 10 = 100;
в) 1100 ? 11 ? 100 = 0.

Вычислите выражения:
а) (11111012 +AF16):368
б) 1258 + 1012 ·2A16 – 1418
Ответ дайте в десятичной системе счисления.

Задачник «Системы счисления»

может быть представлено в виде:
Aq =±(an–1 qn–1 + an–2 

qn–2 +…+ a0  q0 + a–1  q–1 +…+ a–m  q–m).

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит - совокупность цифр системы счисления.

Система счисления

Двоичная

Десятичная

Восьмеричная

Шестнадцатеричная

Римская

Позиционная

ДМПЛ №1 Информатика 8 класс

История развития систем счисления
http://school-collection.edu.ru/catalog/res/1a264912-eca9-4b45-8d77-c3655b199113/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – Перевод недесятичных чисел в десятичную

систему счисления
http://school-collection.edu.ru/catalog/res/78ba290c-0f7c-4067-aaf4-d72f40f49f3b/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 - Перевод десятичных чисел в другие системы счисления
http://school-collection.edu.ru/catalog/res/67cbf74b-f85a-4e9d-88c5-58f203fb90ce/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 - Сложение и вычитание многоразрядных двоичных чисел
http://school-collection.edu.ru/catalog/res/8bb7eefa-4ed9-43fe-aebe-4d6ac67bc6ec/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 - Сложение и вычитание одноразрядных двоичных чисел
http://school-collection.edu.ru/catalog/res/fc77f535-0c00-4871-b67c-fa2ecf567d46/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – Задачник
http://school-collection.edu.ru/catalog/res/a96df437-5ae3-4cab-8c5f-8d4cd78c5775/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 - Развернутая форма записи числа
http://school-collection.edu.ru/catalog/res/19d0fb95-871d-4063-961d-e7dc5725e555/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – Тренировочный тест