Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Неравенства и предельные теоремы
Содержание
- 1. Неравенства и предельные теоремы
- 2. НеравенстваНеравенство Маркова.Для любой случайной величины ξ и для любого ε > 0
- 3. Доказательство.
- 4. Неравенство Чебышёва Для любой случайной величины ξ и для любого ε >0
- 5. ДоказательствоВ неравенствеМаркова (1)подставимвместо ξ ξ –Mξ и возьмем k=2.
- 6. Пример применения неравенства ЧебышёваОценить вероятность того, что
- 7. НеравенстваНеравенство Коши – Буняковского – Шварца.
- 8. Сходимость по вероятностиОпределение. Последовательность случайных величин ξ1,
- 9. Сходимость по вероятностиОбозначение: Замечание:«p» есть сокращение от «probability»
- 10. ПримерПоследовательность случайных величин ξ1, ξ2 ,…, ξn задана законом:
- 11. Закон больших чисел (ЗБЧ)Определение. Говорят, что к
- 12. Смысл: среднее значение случайных величин стремится по
- 13. ЗБЧ в форме ЧебышёваТеорема. Если для последовательности
- 14. Доказательство основано на неравенстве Чебышёва. Надо показать, что выполняется определение сходимости по вероятности.
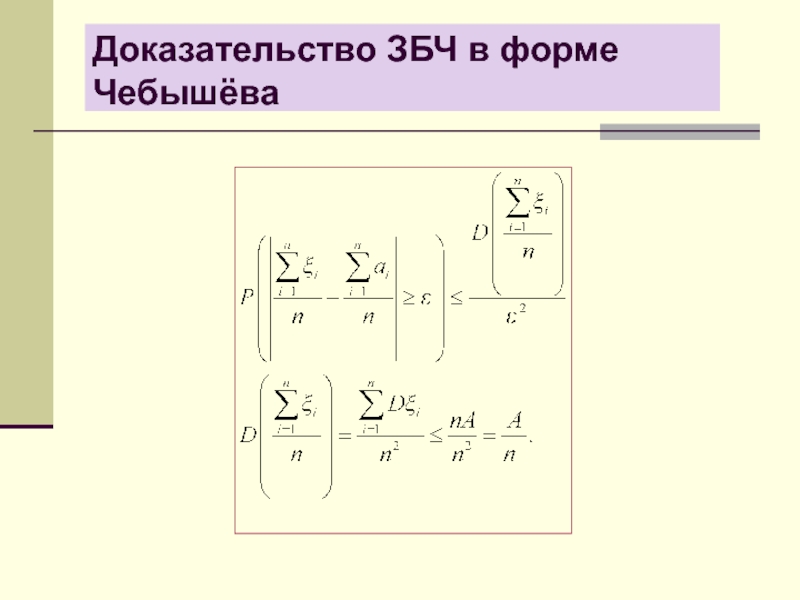
- 15. Доказательство ЗБЧ в форме Чебышёва
- 16. Слайд 16
- 17. ЗБЧ в форме БернуллиТеорема. Пусть осуществляется серия
- 18. Доказательство ЗБЧ в форме БернуллиРассмотрим случайную величину
- 19. ai = Mξi = p. Таким образом, (*) можно записатьв виде (**),что представляетиз себяформулировку ЗБЧ.
- 20. ξi независимы и их дисперсии ограничены одним
- 21. ЗБЧ в форме ПуассонаТеорема. Пусть осуществляется серия
- 22. Доказательство ЗБЧ в форме ПуассонаРассмотрим случайную величину
- 23. ЗБЧ в форме ХинчинаТеорема. Для того, чтобы
- 24. Центральная предельная теорема (ЦПТ)В теоремах этой группы
- 25. Центральная предельная теорема для независимых одинаково распределенных
- 26. Смысл ЦПТ для н.о.р.сл.в.Закон распределения суммы достаточно
- 27. ЦПТТеорема Ляпунова. Если случайная величина ξ
- 28. Смысл ЦПТ в форме ЛяпуноваЗакон распределения суммы
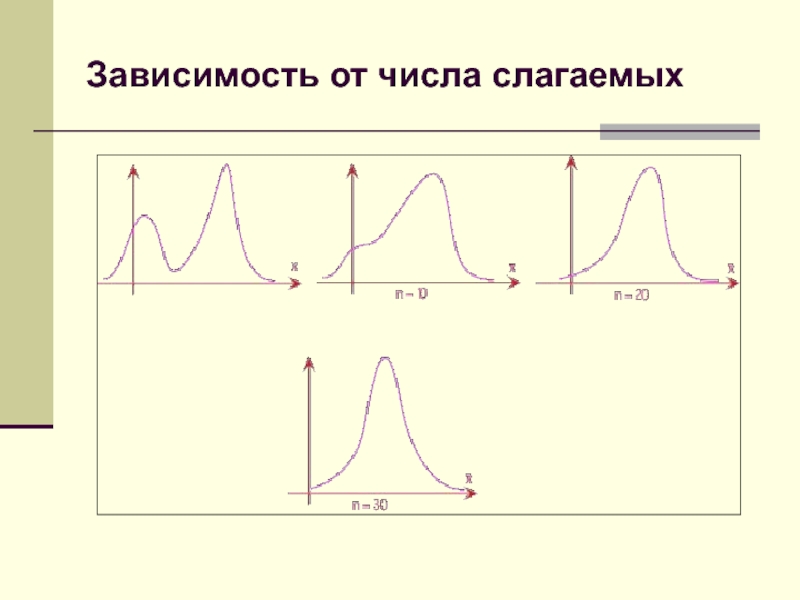
- 29. Зависимость от числа слагаемых
- 30. Практическое значение ЦПТМногие случайные величины можно рассматривать
- 31. валютные курсы;рост, вес животных и растений данного
- 32. Скачать презентанцию
НеравенстваНеравенство Маркова.Для любой случайной величины ξ и для любого ε > 0
Слайды и текст этой презентации
Слайд 6Пример применения неравенства Чебышёва
Оценить вероятность того, что сл.в. отклонится от
своего матожидания
на величину
≥ 2σ,
где σ – средне –квадратичное отклонение.
Слайд 8Сходимость по вероятности
Определение. Последовательность случайных величин ξ1, ξ2 ,…, ξn
сходится по вероятности
к сл. в. ξ, если для
любого ε > 0
Слайд 11Закон больших чисел (ЗБЧ)
Определение. Говорят, что к последовательности случайных величин
ξ1, ξ2 ,…, ξn с математическими ожиданиями Mξi = ai,
i=0,1,…,n, применим закон больших чисел, если
Слайд 12
Смысл: среднее значение случайных величин стремится по вероятности к среднему
их матожиданий (то есть, к постоянной величине).
Замечание. ЗБЧ справедлив при
некоторых условиях. Различные группы условий определяют разные формы закона больших чисел.
Слайд 13ЗБЧ в форме Чебышёва
Теорема. Если для последовательности случайных величин {ξn}
с математическими ожиданиями Mξi=ai
и с
дисперсиями Dξi=σ2i, i=0,1,…,n, выполняются условия:сл.в. {ξn} независимы;
дисперсии всех сл.в. {ξn} ограничены одним и тем же числом, (σ2i ≤ A для всех i),
то к {ξn} применим ЗБЧ, то есть
Слайд 14
Доказательство основано на неравенстве Чебышёва. Надо показать, что выполняется определение
сходимости по вероятности.
Слайд 17ЗБЧ в форме Бернулли
Теорема. Пусть осуществляется серия из n независимых
опытов, проводимых по схеме Бернулли с параметром p, пусть m
– число успехов, m/n – частота успехов в данной серии испытаний. Тогда
Слайд 18Доказательство ЗБЧ в форме Бернулли
Рассмотрим случайную величину ξi, равную числу
успехов в i –ом испытании, i = 1, …, n.
Случайные величины ξi имеют распределение Бернулли. Число успехов в n испытаниях, равное m, можно представить как сумму успехов в отдельных испытаниях.
Слайд 19ai = Mξi = p.
Таким образом,
(*) можно записать
в
виде (**),
что представляет
из себя
формулировку
ЗБЧ.
Слайд 20
ξi независимы и их дисперсии ограничены одним числом
(Dξi = pq < 1)
следовательно,
выполняются
условия ЗБЧв форме
Чебышёва.
Слайд 21ЗБЧ в форме Пуассона
Теорема. Пусть осуществляется серия из n независимых
опытов, причем вероятность успеха в i –м опыте равна
pi. Пусть m – число успехов, m/n – частота успехов в данной серии испытаний. Тогда
Слайд 22Доказательство ЗБЧ в форме Пуассона
Рассмотрим случайную величину ξi, равную числу
успехов в i–м испытании, i =1, …, n.
Случайные
величины ξi имеют распределение Бернулли, ai = Mξi = pi. Замечание. Единственное отличие от предыдущей теоремы – что величины имеют различные матожидания ai = Mξi = pi и различные дисперсии Dξi = piqi.
Доказательство проводится как в предыдущем случае.
Слайд 23ЗБЧ в форме Хинчина
Теорема. Для того, чтобы к последовательности
случайных величин
{ξn} был применим ЗБЧ,
достаточно, чтобы:
сл.в. {ξn} независимы;
сл.в. {ξn} одинаково распределены.
Тогда
Слайд 24Центральная предельная теорема (ЦПТ)
В теоремах этой группы выясняются условия, при
которых возникает нормальное распределение. Общим для этих теорем является следующее
обстоятельство: закон распределения суммы достаточно большого числа независимых случайных величин при некоторых условиях неограниченно приближается к нормальному.
Слайд 25Центральная предельная теорема для независимых одинаково распределенных сл. в.
Если случайные
величины {ξn} независимы, одинаково распределены и имеют конечные математические ожидания
Mξi=a и дисперсии Dξi=σ2,… i=0,1,…,n, то при n→∞
Слайд 26Смысл ЦПТ для н.о.р.сл.в.
Закон распределения суммы достаточно большого числа независимых
одинаково распределенных случайных величин приближается к нормальному закону.
При числе
слагаемых около 10 закон распределения суммы уже близок к нормальному.
Слайд 27ЦПТ
Теорема Ляпунова. Если случайная величина ξ представляет собой сумму
большого числа независимых случайных величин ξ1, ξ2,…,ξn, влияние каждой из
которых на всю сумму равномерно мало, то величина ξ имеет распределение, близкое к нормальному, и тем ближе, чем больше n.
Слайд 28Смысл ЦПТ в форме Ляпунова
Закон распределения суммы достаточно большого числа
независимых случайных величин, каждая из которых мало влияет на сумму,
приближается к нормальному закону.При этом важно то, что законы распределения суммируемых случайных величин могут быть любыми, заранее не известными исследователю.
При числе слагаемых около 10 закон распределения суммы уже близок к нормальному.
Слайд 30Практическое значение ЦПТ
Многие случайные величины можно рассматривать как сумму отдельных
независимых слагаемых.
Например:
ошибки различных измерений;
отклонения размеров деталей, изготовляемых
при неизменном технологическом режиме; распределение числа продаж некоторого товара, объемов прибыли от реализации однородного товара различными производителями;
Слайд 31
валютные курсы;
рост, вес животных и растений данного вида;
отклонение точки
падения снаряда от цели. Из ЦПТ следует, что они могут
рассматриваться как суммарный результат большого числа слагаемых и потому приближенно следовать нормальному закону распределения.
