Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нормальный закон распределения
Содержание
- 1. Нормальный закон распределения
- 2. План лекции:Закономерности нормального распределенияКривая нормального распределения и
- 3. Нормальный закон распределения случайных величин Нормальное
- 4. ЗАКОНОМЕРНОСТИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ:Параметр μ характеризует математическое ожидание
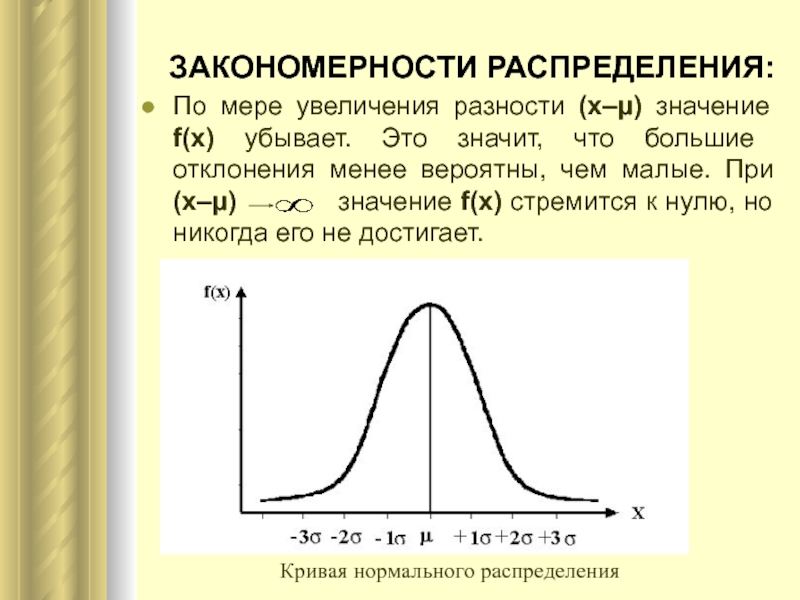
- 5. ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ:По мере увеличения разности (x–μ) значение
- 6. Функция распределения вероятностей:Функция плотности распределения вероятностей:
- 7. Вероятность попадания значения случайной величины
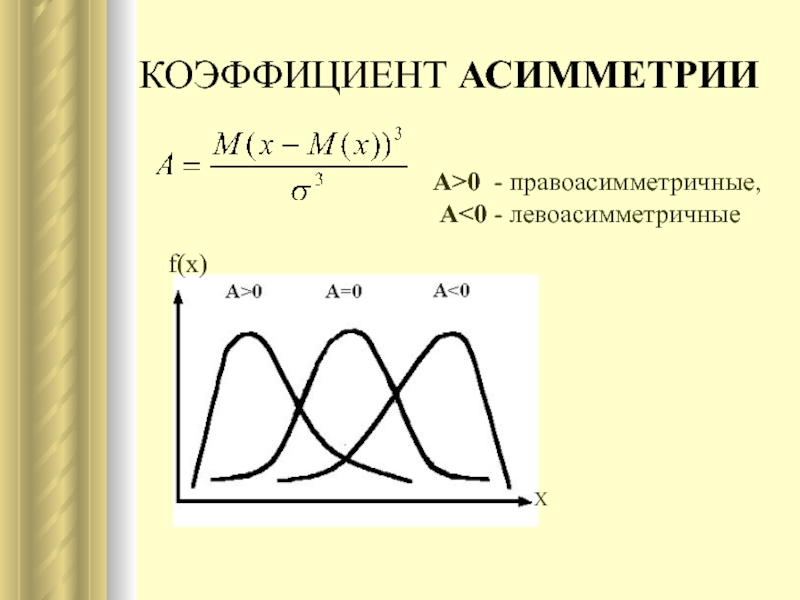
- 8. КОЭФФИЦИЕНТ АСИММЕТРИИ А>0 - правоасимметричные, А
- 9. ПОКАЗАТЕЛЬ ЭКСЦЕССАf(x)Х
- 10. Интервальные оценкинормированное отклонениех – μ=σt1σ – 68,3%;
- 11. Доверительные вероятности и доверительные интервалыВероятности 0,95 и
- 12. Генеральная и выборочные совокупностиНаиболее общую совокупность, подлежащих
- 13. Сравнительная характеристикаСредняя квадратическая ошибка (стандартная ошибка)sσСреднее квадратическое отклонениеμМатематическоеожиданиеВыборочнаяГенеральнаяСовокупностьХарактеристикизначение генеральной средней с доверительным интервалом
- 14. Сравнение теоретических и эмпирических распределенийНулевая гипотеза. Согласно
- 15. Средние квадратические ошибки sА (асимметрии) и
- 16. Сравнение теоретических и экспериментальных
- 17. Критерий Пирсона где mi – экспериментальные
- 18. Число степеней свободы – это общее число
- 19. Основные этапы исследования: Сгруппировать исследуемый ряд
- 20. БЛАГОДАРЮ ЗА ВНИМАНИЕ
- 21. Скачать презентанцию
План лекции:Закономерности нормального распределенияКривая нормального распределения и ее характеристикиИнтервальные оценкиГенеральная и выборочная совокупностиСравнение теоретических и эмпирических распределенийОсновные этапы исследования
Слайды и текст этой презентации
Слайд 2План лекции:
Закономерности нормального распределения
Кривая нормального распределения и ее характеристики
Интервальные оценки
Генеральная
и выборочная совокупности
Слайд 3Нормальный закон распределения случайных величин
Нормальное распределение возникает тогда,
когда на изменение случайной величины действует множество различных независимых факторов,
каждый из которых в отдельности не имеет преобладающего значения.Слайд 4ЗАКОНОМЕРНОСТИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ:
Параметр μ характеризует математическое ожидание (среднее арифметическое) случайной
величины, являясь центром распределения и наиболее вероятным значением. Изменение математического
ожидания не влияет на форму кривой, а только вызывает ее смещение вдоль оси x.Параметр σ характеризует изменчивость случайной величины (меру растянутости кривой вдоль оси x): чем больше σ, тем больше кривая растянута.
График нормальной кривой симметричен относительно прямой x=μ (одинаковые по абсолютной величине отрицательные и положительные отклонения случайной величины от центра равновероятны).
Слайд 5ЗАКОНОМЕРНОСТИ РАСПРЕДЕЛЕНИЯ:
По мере увеличения разности (x–μ) значение f(x) убывает. Это
значит, что большие отклонения менее вероятны, чем малые. При (x–μ)
значение f(x) стремится к нулю, но никогда его не достигает. Кривая нормального распределения
Слайд 7 Вероятность попадания значения случайной величины в интервал от
а до b:
причем Ф(–t) = 1– Ф(t)
Характеристики
кривой:Коэффициент асимметрии
Показатель эксцесса
Слайд 10Интервальные оценки
нормированное отклонение
х – μ=σt
1σ – 68,3%;
2σ – 95,5%;
3σ – 99,7% всех вариант
Слайд 11Доверительные вероятности и доверительные интервалы
Вероятности 0,95 и 0,99 (95% и
99%) – доверительные вероятности
Δх=±σt – доверительный интервал
α=1 – Р
уровень значимостиСлайд 12Генеральная и выборочные совокупности
Наиболее общую совокупность, подлежащих изучению объектов называют
генеральной.
Выборка считается репрезентативной, если каждый объект выборки отобран случайно из
генеральной совокупности, то есть все объекты имеют одинаковую вероятность попасть в выборку.Слайд 13Сравнительная характеристика
Средняя квадратическая ошибка (стандартная ошибка)
s
σ
Среднее квадратическое отклонение
μ
Математическое
ожидание
Выборочная
Генеральная
Совокупность
Характеристики
значение генеральной средней
с доверительным интервалом
Слайд 14Сравнение теоретических и эмпирических распределений
Нулевая гипотеза. Согласно этой гипотезе первоначально
принимается, что между эмпирическим и теоретическим распределением признака в генеральной
совокупности достоверного различия нет.Слайд 15Средние квадратические ошибки
sА (асимметрии) и sЕ (эксцесса)
Для
достаточно большой выборки (n>30), если показатели асимметрии (А) и эксцесса
(Е) в два и более раза превышают показатели их средних квадратических ошибок, гипотезу о нормальности распределения нужно отвергнуть.
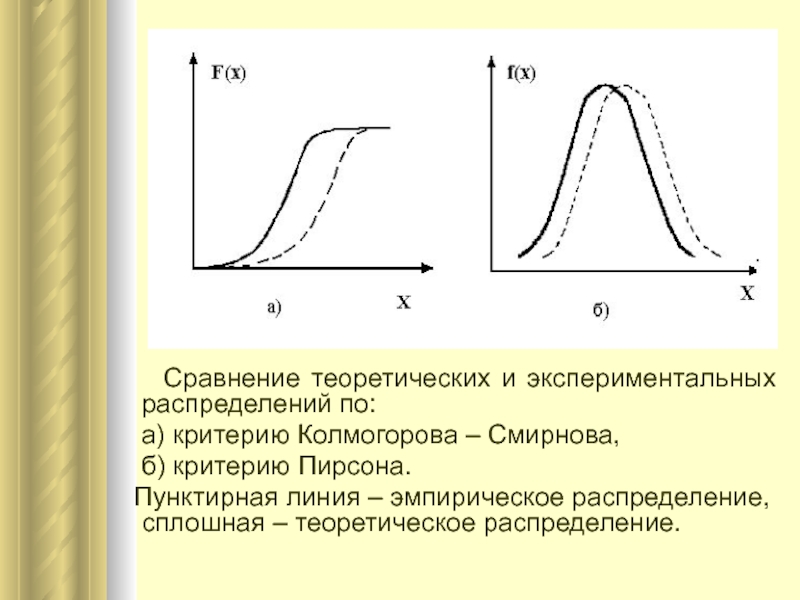
Слайд 16 Сравнение теоретических и экспериментальных распределений по:
а) критерию Колмогорова – Смирнова,
б) критерию
Пирсона. Пунктирная линия – эмпирическое распределение, сплошная – теоретическое распределение.
Слайд 17Критерий Пирсона
где mi – экспериментальные частоты попадания значения
случайной величины в интервал,
npi – теоретические частоты.
Слайд 18Число степеней свободы – это общее число величин, по которым
вычисляются соответствующие статистические показатели, минус число тех условий, которые связывают
эти величины, то есть уменьшают возможности вариации между ними. Число степеней свободы определяется по следующей формуле:df=k–r–1, где k – число интервалов, r – число параметров предполагаемого распределения. Для нашего случая r=2, следовательно, df=k–3.
По заданному уровню значимости (α) и числу степеней свободы df, находим критическое значение χ2кр (α,df).
Если χ2эмп <χ2кр гипотеза о согласии эмпирического и теоретического распределения не отвергается.
Слайд 19
Основные этапы исследования:
Сгруппировать исследуемый ряд по классам. Подсчитать середины интервалов
и частоты попадания в интервал.
Построить гистограмму и полигон распределения.
Найти
эмпирическую функцию распределения и построить ее график. Вычислить числовые (точечные) характеристики распределения.
Найти интервальные оценки для генеральной средней.
Проверить гипотезу о том, что генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону, используя критерий Пирсона χ2.