Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Область определения и область изменения функции. Ограниченность функции
Содержание
- 1. Область определения и область изменения функции. Ограниченность функции
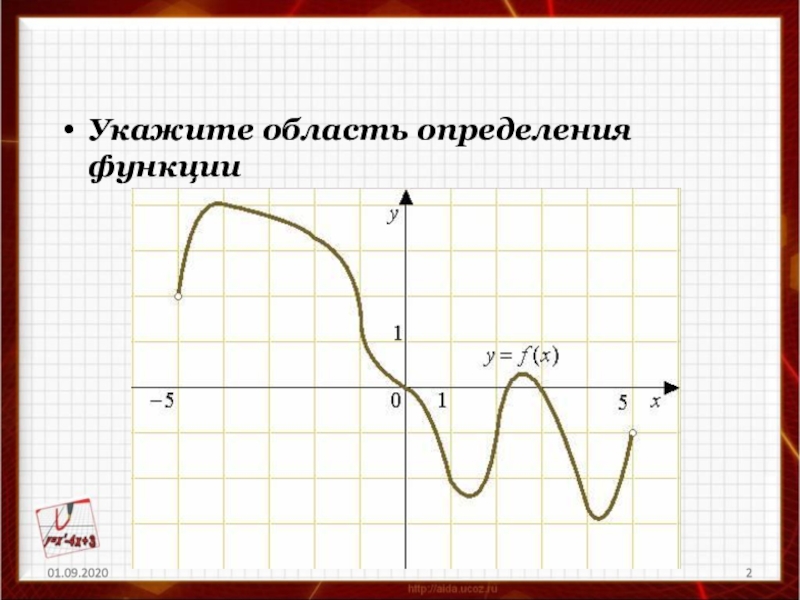
- 2. Укажите область определения функции
- 3. Устно:Даны элементарные функции:Задайте сложную функцию:
- 4. Устно:Вычислите значение сложной функции:
- 5. Область определения функцииОбласть определения функции обозначают Х
- 6. Область определения функцииПолной областью определения функции, заданной
- 7. Примеры:Найдите область определения функции:
- 8. Примеры:Найдите область определения функции:, т.к. -1≤sinx≥1,то
- 9. Область изменения(область значений) функцииОбласть изменения функции f(x)
- 10. Примеры:Найдите область изменения функции:
- 11. Примеры:Найдите область определения функции:
- 12. Ограниченность функцииФункцию у= f(x) , определенную на
- 13. Ограниченность функции Примеры:Функция у= х2 , определенная
- 14. Ограниченность функцииФункцию у= f(x) , определенную на
- 15. Ограниченность функции Примеры:Функция у=- х2 , определенная
- 16. Ограниченность функцииФункцию у= f(x) , определенную на
- 17. Ограниченность функции Примеры:Функция у=sinx, определенная на множестве
- 18. Наименьшее и наибольшее значение функцииПро функцию у=
- 19. Примеры:Функция у= х2 , определенная на множестве
- 20. Примеры:Функция у= 2х , определенная на множестве R, не принимает наименьшего значения, ограничена снизу числом 0.
- 21. Примеры:Функция у= log2x , определенная на множестве R+, не принимает ни наименьшего ни наибольшего значения.
- 22. Упражнения:Стр. 7№1.8(г-е)№1.9(г-е)№1.10(а-г)№1.14(а-в)
- 23. Домашнее задание:Стр. 7№1.8(а-в) №1.10(д-з) №1.12(в)№1.14(г-е)
- 24. Скачать презентанцию
Укажите область определения функции
Слайды и текст этой презентации
Слайд 5Область определения функции
Область определения функции обозначают Х или D(f).
Иногда ,
задавая функцию аналитически не указывают явно ее область определения.
случаях рассматривают функцию на ее полной области определения.
Слайд 6Область определения функции
Полной областью определения функции, заданной аналитически называют множество
всех действительных значений независимой переменной х, для каждого из которых
функция принимает действительные значения.Полную область определения называют областью существования функции.
Слайд 9Область изменения(область значений) функции
Область изменения функции f(x) называют множество всех
чисел f(x) , соответствующих каждому х из области определения функции.
Область
изменения функции f(x) обозначают У или Е(f).
Слайд 12Ограниченность функции
Функцию у= f(x) , определенную на множестве Х, называют
ограниченной снизу на множестве Х, если существует число А, такое,
что А≤f(x) для любого х из множества Х
Слайд 13Ограниченность функции
Примеры:
Функция у= х2 , определенная на множестве R, ограниченa
снизу, т.к. х2 ≥0, для любого действительного числа.
Слайд 14Ограниченность функции
Функцию у= f(x) , определенную на множестве Х, называют
ограниченной сверху на множестве Х, если существует число В, такое,
что f(x)≤В для любого х из множества Х
Слайд 15Ограниченность функции
Примеры:
Функция у=- х2 , определенная на множестве R, ограниченa
сверху, т.к. -х2 ≤0, для любого действительного числа.
Слайд 16Ограниченность функции
Функцию у= f(x) , определенную на множестве Х, называют
ограниченной на множестве Х, если существует число М, такое, что
│f(x)│≤М для любого х из множества Х
Слайд 17Ограниченность функции
Примеры:
Функция у=sinx, определенная на множестве R, ограниченa на всей
области существования, т.к. │sinx│≤1, для любого действительного числа.
Слайд 18Наименьшее и наибольшее значение функции
Про функцию у= f(x) говорят,что она
принимает на множестве Х, наименьшее значение в точке х0, если
Про
функцию у= f(x) говорят,что она принимает на множестве Х, наибольшее значение в точке х0, если
Слайд 19Примеры:
Функция у= х2 , определенная на множестве R, принимает наименьшее
значение у=0 при х=0. наибольшего значения нет, не ограничена сверху.
Слайд 20Примеры:
Функция у= 2х , определенная на множестве R, не принимает
наименьшего значения, ограничена снизу числом 0.
Слайд 21Примеры:
Функция у= log2x , определенная на множестве R+, не принимает
ни наименьшего ни наибольшего значения.
