Слайд 1ОБЩИЕ ПОНЯТИЯ
НЕЛИНЕЙНОЙ ТЕОРИИ КОЛЕБАНИЙ
Часть 1
Слайд 2Рассматриваемые вопросы
О предмете теории колебаний
О предмете теории колебаний
Нелинейные элементы и
нелинейные характеристики
Фундаментальные эффекты, к которым приводит нелинейность
Неизохронность
Ангармоничность колебаний и генерация
гармоник
Комбинационные составляющие
Автоколебания
Бифуркации, мультистабильность и гистерезис
Динамический хаос
Слайд 3О предмете теории колебаний
О предмете теории колебаний
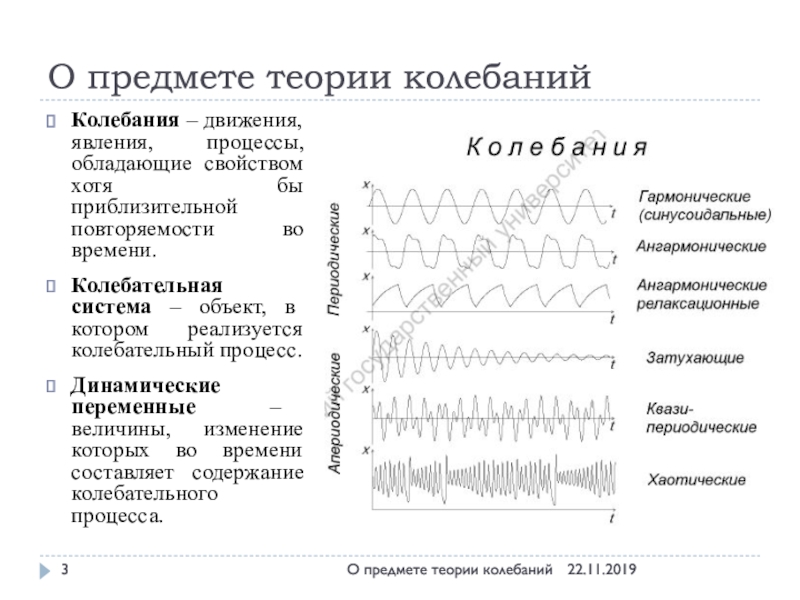
Колебания – движения, явления,
процессы, обладающие свойством хотя бы приблизительной повторяемости во времени.
Колебательная
система – объект, в котором реализуется колебательный процесс.
Динамические переменные – величины, изменение которых во времени составляет содержание колебательного процесса.
Слайд 4О предмете теории колебаний
О предмете теории колебаний
Слайд 5О предмете теории колебаний
О предмете теории колебаний
Малые колебания протекают одинаково
Параметр
ω определяется формой лунки в близи ее
дна; Решением служит функция вида
Большие колебания происходят по-разному
Происходит добавление в уравнение нелинейных членов
С ростом амплитуды «включается» нелинейность
Малые колебания составляют предмет линейной, а большие – нелинейной теории колебаний.
Слайд 6О предмете теории колебаний
О предмете теории колебаний
Примеры систем, для которых
малые колебания не являются линейными (атипичная ситуация, при которой коэффициент
разложения в ряд Тейлора перед квадратичным членом обращается в ноль):
А) профиль лунки имеет разложение в ряд, начиная с четвертой степени
Б) профиль со скачком первой производной в нижней точке
В) профиль со скачком второй производной в нижней точке
Слайд 7О предмете теории колебаний
О предмете теории колебаний
Линейные уравнения содержат только
первые степени динамических переменных и их производных.
Если функции x1(t) и
x2(t) являются решениями, то каждая линейная комбинация вида с1x1(t) и с2x2(t) также служит решением (принцип суперпозиции).
По-настоящему линейных систем в природе не бывает.
В линейной системе среди определяющих величин нет параметра с размерностью амплитуды => колебания разной амплитуды должны происходить одинаковым образом.
В нелинейной системе принцип суперпозиции не выполняется => колебания будут протекать по-разному в зависимости от того, мала или велика их амплитуда.
Слайд 8О предмете теории колебаний
О предмете теории колебаний
Параметры – постоянные во
времени величины, от задания которых может зависеть характер реализующегося в
системе режима.
Динамическая система – любой объект или процесс, для которого однозначно определено понятие состояния, как совокупности некоторых величин в некоторый момент времени, и задан закон (динамика), описывающий эволюцию начального состояния с течением времени.
Если рассматривать точки x1, x2, … , xN как координаты точки x в N-мерном пространстве, то получается наглядное геометрическое представление состояния динамической системы в виде этой точки. Последнюю называют изображающей (фазовой) точкой, а пространство состояний – фазовым пространством ДС.
Динамика системы представляется движением изображающей точки в ФП по некоторой траектории, называемой фазовой траекторией (орбитой).
Слайд 9О предмете теории колебаний
О предмете теории колебаний
Колебательные системы:
Консервативные: полная механическая
энергия остается с течением времени постоянной.
Диссипативные: имеются потери механической энергии
из-за трения.
Колебательная система произвольной природы считается консервативной, либо диссипативной, если ее динамика описывается такой математической моделью, которая соответствует в точности некоторой консервативной, либо диссипативной, механической системе.
Консервативная система (прим. электрическая цепь, содержащая только реактивные элементы): характерно неограниченно долгое сохранение «памяти» о начальном состоянии.
Диссипативная система (прим. электрическая цепь, содержащая сопротивления (резисторы)): характерна «потеря памяти» о начальном состоянии. Множество точек в фазовом пространстве диссипативной системы, посещаемых в установившемся режиме, называется аттрактором (прим. устойчивое состояние равновесия и устойчивый предельный цикл).
Слайд 10О предмете теории колебаний
О предмете теории колебаний
Автоколебания - незатухающие колебания
в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за
счёт энергии постоянного, то есть непериодического внешнего воздействия. Характеристики автоколебаний (амплитуда, частота, форма колебаний) определяются параметрами самой системы и не зависят от конкретных начальных условий.
Слайд 11О предмете теории колебаний
О предмете теории колебаний
На раннем этапе теории
колебаний казалось, что нелинейные системы слишком разнообразны, чтобы допускать анализ
с каких-то единых позиций. Идея о том, что возможно построение общей теории нелинейных колебаний была неочевидной, революционной.
Леонид Исаакович Мандельштам (1879–1944) – советский физик, основатель научной школы.
идея выработки нелинейного мышления — совокупности концепций, представлений, моделей, методов, которые составляли бы содержание единого подхода к исследованию нелинейных колебаний в системах различной природы.
Александр Александрович Андронов (1901–1952) – основоположник ТК, ученик Мандельштама.
Книга Мандельштама “Лекции по теории колебаний” и книга Андронова, Витта и Хайкина “Теория колебаний”.
Слайд 12О предмете теории колебаний
О предмете теории колебаний
Для ТК одна из
первостепенных задач - конструирование модели колебательной системы, основанное на правильной
идеализации реального процесса.
ХХ век – бурное развитие ТК
чрезвычайно разрослась база применения идей ТК
Изменение содержания и методического инструментария ТНК (привлечение методов численного моделирования)
центр интереса сместился от систем с минимальным количеством существенных динамических переменных (маломерных) к системам с большим их количеством (многомерным). Обнаруживается, что начиная с размерности ФП, равной трем, становятся возможными нетривиальные типы колебательных процессов. В частности, могут наблюдаться хаотические колебания или динамический хаос.
Динамический хаос характеризуется сложной, нерегулярной зависимостью динамических переменных от времени, и при этом обладает высокой чувствительностью к малым возмущениям начальных условий.
Слайд 13О предмете теории колебаний
О предмете теории колебаний
Нелинейная динамика
Дисциплина более
математического характера, нежели ТК.
Основное содержание нелинейной динамики — исследование математических
моделей различных систем.
Некоторое смещение внимания к более современным аспектам сложного динамического поведения, ставшим доступными для анализа в эпоху компьютеров (например, динамический хаос).
Слайд 14О предмете теории колебаний
О предмете теории колебаний
Синергетика, теория диссипативных структур
В
70-х гг. XX века немецкий ученый, специалист в области лазерной
физики, Герман Хакен усмотрел аналогию между процессами возникновения генерации в лазере и формированием структур в системах иной природы. Он провозгласил, что это может служить основой новой синтетической научной дисциплины — синергетики.
Предмет синергетики во многом совпадает с предметом теории колебаний и волн, но ее специфика состоит в особом внимании к феномену самоорганизации (речь идет о процессах, заключающихся в самопроизвольном формировании и усложнении упорядоченных структур).
Проблема того, каким образом динамика индивидуальных элементов и характер связи между ними проявляется в свойствах среды, ее способности к образованию пространственных структур, – одна из центральных задач синергетики.
Слайд 15Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Для понимания поведения
сложных объектов имеет смысл представлять объект как совокупность составных частей,
элементов, каждый из которых может быть охарактеризован совокупностью только тех его свойств, которые существенны для функционирования системы в целом.
Пример. Рассмотрим радиоприемник или телевизор, представляющий собой сложную систему из соединенных определенным образом элементов – транзисторов, конденсаторов, резисторов и др. Рассматривая принципиальную схему, мы не вспоминаем о явлениях, происходящих внутри каждого транзистора, диода или иного элемента. То, что для нас в данный момент имеет значение, это не внутреннее устройство элементов, а их “внешние” свойства и характеристики, существенные для функционирования схемы.
Слайд 16Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Величину f можно
трактовать как воздействие, а величину dv/dt — как отклик. Зависимость
отклика от воздействия линейная, определяется единственным параметром — коэффициентом пропорциональности m.
Величину силы интерпретируем как воздействие, а удлинение — как отклик. Зависимость отклика от воздействия линейная и определяется коэффициентом жесткости пружины k.
Элемент вязкого трения, характеризуется линейной зависимостью скорости от приложенной силы f: fv=α, где константа есть коэффициент трения
Слайд 17Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
q=CU. Ток I
есть производная по времени от накопленного заряда, так что можно
написать I=C*dU/dt.
Катушка индуктивности характеризуется линейной зависимостью между производной от протекающего тока dI/dt и величиной приложенного напряжения U. Коэффициент пропорциональности есть индуктивность L: L*dU/dt=I.
U=RI или I=gU, где R называется сопротивлением, а об-ратная величина g=1/R — проводимостью.
Слайд 18Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Слайд 19Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Каждому из рассмотренных
механических и электрических элементов соответствует линейная и притом мгновенная, безынерционная
связь величин, представляющих воздействие и отклик.
Безынерционное (пропорциональное) звено – звено, для кот. в любой момент t выходная величина пропорциональна входной.
Простейшее обобщение состоит в том, чтобы считать связь между воздействием и откликом нелинейной, хотя по-прежнему мгновенной.
Если ограничиться малым интервалом изменения силы и удлинения, то можно ввести дифференциальный коэффициент жесткости, как отношение изменения силы к изменению удлинения. kдиф=df/dx.
Гистерезис – зависимость между воздействием и откликом оказывается зависящей от предыстории.
Слайд 20Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Нелинейность в механической
системе может вноситься также благодаря трению. Известно, что при обтекании
тел жидкостью прямая пропорциональность между скоростью и силой имеет место только при малых скоростях (закон Стокса). При больших скоростях он модифицируется, и в определенном диапазоне скоростей сила оказывается приблизительно пропорциональна квадрату скорости, так что можно записать
Слайд 21Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Определенном приближении (закон
Кулона — Амонтона) силу сухого трения считают постоянной по величине
и противоположной по направлению скорости относительного движения тел. Таким образом, связь между воздействием (приложенной силой) и откликом (скоростью), т.е. нелинейная характеристика для элемента сухого трения, выражается соотношением
Слайд 22Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Частица, ускоряющаяся под
действием приложенной силы, выступает как элемент нелинейный, если принять во
внимание установленную в теории относительности релятивистскую зависимость массы от скорости:
Нелинейную характеристику такого элемента удобно представлять функцией, определяющей зависимость импульса от скорости,
Слайд 23Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Слайд 24Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Слайд 25Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Слайд 26Нелинейные элементы и нелинейные характеристики
О предмете теории колебаний
Слайд 27Фундаментальные эффекты, к которым приводит нелинейность
О предмете теории колебаний
Особенность нелинейных
систем состоит в том, что в них колебания разной амплитуды
могут быть существенно различными по своим характеристикам.
Общие конкретные эффекты, посредством которых может проявлять себя нелинейность:
неизохронность
ангармоничность
мультистабильность
автоколебания
динамический хаос
Слайд 28Фундаментальные эффекты, к которым приводит нелинейность. Неизохронность
О предмете теории колебаний
Неизохронность
- свойство, которое заключается в том, что период колебаний оказывается
зависящим от амплитуды.
Маятник как пример неизохронной колебательной системы:
определение основных параметров (а),
зависимость момента возвращающей силы от угла отклонения (б),
зависимость периода колебаний от амплитуды – угла максимального отклонения (в),
иллюстрация колебаний с отклонением на большой угол (г).
Слайд 29Фундаментальные эффекты, к которым приводит нелинейность. Неизохронность
О предмете теории колебаний
Высоту
подпрыгивания примем за амплитуду. Время падения тела в поле тяжести
с высоты А без начальной скорости равно и совпадает со временем подъема, так что период колебаний составит , т.е. он пропорционален корню квадратному из амплитуды. Таким образом, колебания не-изохронные.
Неизохронность - свойство, которое заключается в том, что период колебаний оказывается зависящим от амплитуды.
Слайд 30Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Ангармонические колебания – колебания, форма которых отличается
от синусоиды.
Вид временных зависимостей угла отклонения маятника при раз-ной амплитуде колебаний:
При малой амплитуде колебания близки к гармоническим.
При больших амплитудах форма колебаний становится заметно отличной от синусоиды, т.е. колебания оказываются ангармоническими.
Слайд 31Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Спектральное представление колебаний.
Слайд 32Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Член ряда (3.8) с нулевым индексом отвечает
постоянной составляющей – представляет собой среднее значение функции за период.
Если отличен от нуля один только первый член суммы, то это соответствует гармоническим колебаниям.
Если же сумма содержит другие ненулевые члены, то колебания ангармонические.
Чаще всего самую большую амплитуду имеет первый член. Его считают основной гармонической составляющей процесса, и говорят о ней как о первой гармонике. (Гармоника – отдельная синусоидная величина.)
Частота колебаний m-ой гармоники равна mω.
Слайд 33Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Коэффициент нелинейных искажений - количественная характеристика отклонения
колебательного процесса от гармонических колебаний.
Ангармоничность трактуется как присутствие составляющих с частотами 2ω, 3ω, ..., — высших гармоник. Появление высших гармоник можно связать с преобразованием спектра периодического сигнала нелинейными элементами.
Слайд 34Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Слайд 35Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Квадратичная нелинейность отвечает за появление постоянной составляющей
(детектирование – отделение полезного (модулирующего) сигнала от несущей составляющей; преобразование электрических колебаний, в результате которого получаются колебания более низкой частоты) и второй гармоники. Соответствующие слагаемые в формуле (3.17) пропорциональны коэффициенту квадратичной нелинейности a2 и квадрату входной амплитуды.
Кубическая нелинейность обеспечивает нелинейную добавку к амплитуде основной гармоники и возникновение третьей гармоники. Соответствующие слагаемые пропорциональны коэффициенту кубической нелинейности a3 и кубу входной амплитуды.
Слайд 36Фундаментальные эффекты, к которым приводит нелинейность. Ангармоничность колебаний и генерация
гармоник
О предмете теории колебаний
Преобразование входного гармонического сигнала элементами с линейной,
квадратичной и кубической характеристиками
Слайд 37Фундаментальные эффекты, к которым приводит нелинейность. Комбинационные составляющие
О предмете теории
колебаний
Сигнал, представляющий собой суперпозицию двух гармонических составляющих с частотами ω1
и ω2
Предположим, что нелинейная характеристика квадратичная
Подставляя сюда выражение для x(t), получаем
Преобразуем квадраты и произведения синусов так, чтобы выражение содержало элементарные тригонометрические функции только в первой степени.
Слайд 38Фундаментальные эффекты, к которым приводит нелинейность. Комбинационные составляющие
О предмете теории
колебаний
Если входной сигнал содержит множество составляющих с частотами ω1, ω2,
… ωN, то в результате квадратичного нелинейного преобразования получатся комбинационные составляющие со всевозможными частотами ωm ±ωn, амплитуды которых будут определяться произведением соответствующих амплитуд Аm и Аn.
Составляющая на частоте ωm ± ωn интерпретируется как результат взаимодействия компонент входного сигнала с частотами ωm и ωn.
Постоянную составляющую (Аm)^2 и вторую гармонику на частоте 2ωm можно трактовать как результат самовоздействия частотной составляющей ωm.
Слайд 39Фундаментальные эффекты, к которым приводит нелинейность. Комбинационные составляющие
О предмете теории
колебаний
Случай кубической нелинейности.
Если входной сигнал содержит множество составляющих с частотами
ω1, ω2, … ωN, то действие кубической нелинейности приводит к появлению комбинационных составляющих с частотами ωm ± ωn ± ωk.
Амплитуды комбинационных составляющих определяются произведением амплитуд Аm, Аn, и Аk.
В частности, самовоздействие одной из гармонических составляющих входного сигнала ωm выражается в появлении компоненты выходного сигнала на той же частоте (ωm + ωn - ωk) и третьей гармоники (ωm + ωn + ωk).
Слайд 40Фундаментальные эффекты, к которым приводит нелинейность. Автоколебания
О предмете теории колебаний
Автоколебания
- самопроизвольно возникающий в некоторых диссипативных системах колебательный процесс, характеристики
которого определяются свойствами самой системы и не зависят от конкретных начальных условий.
Энергия необходимая для поддержания процесса черпается из неколебательного источника. Автоколебательный процесс – всегда принципиально нелинейный феномен.
Слайд 41Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Параметры - величины, которые считаются постоянными во времени,
но от задания которых может зависеть характер реализующегося в системе режима.
Бифуркация - качественное изменение режима при изменении параметра. Процесс изменения параметров можно мыслить как движение по определенной траектории в пространстве, где по осям координат отложены параметры системы.
Пространство параметров VS Фазовое пространство. В первом случае по осям координат откладываются параметры, а во втором – динамические переменные системы.
Слайд 42Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Одна из распространенных и хорошо изученных бифуркаций связана
с возникновением автоколебаний.
Малые колебания вблизи состояния равновесия перестают затухать и становятся нарастающими.
В этих условиях любое случайное начальное возмущение даст «затравку» колебательному процессу. Появятся сначала колебания малой амплитуды, затем амплитуда будет нарастать до тех пор пока она не стабилизируется на определенном уровне из-за нелинейных эффектов.
Бифуркацию рождения периодических автоколебаний называют бифуркацией Андронова — Хопфа. Формальное содержание этой бифуркации состоит в том, что существовавшая ранее в фазовом пространстве системы неподвижная точка теряет устойчивость, а аттрактором становится замкнутая фазовая траектория – предельный цикл.
Слайд 43Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
В присутствии трения шарик будет совершать колебания вблизи
точки минимума, приходя в состояние устойчивого равновесия.
Если профиль имеет более одного минимума, устойчивых состояний равновесия тоже будет несколько.
Тогда мы имеем дело с колебательной системой, имеющей несколько разных сосуществующих аттракторов, в качестве которых в нашем простом примере выступают состояния устойчивого равновесия.
Каждому аттрактору отвечает определенный бассейн притяжения – область значений начальных координаты и скорости, соответствующая тому, что в итоге частица окажется в определенной лунке.
Слайд 44Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Если какая-нибудь колебательная система характеризуется наличием нескольких разных
потенциально возможных установившихся состояний или колебательных режимов, и возникновение того или иного из них зависит только от задания начальных условий, то говорят, что имеет место мультистабильность.
В линейной системе мультистабильность невозможна.
Слайд 45Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Предположим, что форму профиля можно регулировать, изменяя параметры
системы, так что в процессе этой деформации могут появляться или пропадать локальные минимумы.
Одно из интересных явлений будет наблюдаться в ситуации, когда ямка, в которой располагается шарик, сближается с локальным максимумом, сливается с ним, и исчезает. Это бифуркация слияния устойчивого (минимум) и неустойчивого (максимум) состояний равновесия.
После бифуркации локальный минимум исчезает, и система должна скачком перейти в новое состояние, достаточно удаленное от исходного.
Слайд 46Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Слайд 47Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Слайд 48Фундаментальные эффекты, к которым приводит нелинейность. Бифуркации, мультистабильность и гистерезис.
О
предмете теории колебаний
Рис. 3.17. К пояснению явлений, наблюдаемых при обходе
точки сборки в разных направлениях.
Рис.3.18. Изменение потенциального рельефа, соответствующее двум траекториям движения по плоскости параметров, приводящим к реализации двух различных состояний устойчивого равновесия.
При этом скачкообразное изменение состояния, о котором говорят как о жесткой бифуркации или катастрофе, происходит при пересечении одной линии складок при движении слева направо и другой при движении справа налево.
Слайд 49Фундаментальные эффекты, к которым приводит нелинейность. Динамический хаос
О предмете теории
колебаний
Несовпадающие фазовые траектории отвечают разной по характеру динамике: они посещают
разные области фазового пространства, а нелинейность и заключается в том, что в разных областях поток траекторий устроен по-разному.
В нелинейных системах с числом динамических переменных более трех в определенных случаях может встречаться такой тип динамического поведения, когда любые два движения, характеризуемые близкими начальными условиями, постепенно уходят друг от друга так, что через определенное время они становятся существенно различными. Если этим свойством обладают все фазовые траектории, доступные в данном режиме функционирования системы, то она демонстрирует динамический хаос.
Слайд 50Фундаментальные эффекты, к которым приводит нелинейность. Динамический хаос
О предмете теории
колебаний
Динамический хаос - режим, характеризующийся нерегулярным, похожим на случайный процесс,
изменением динамических переменных во времени, и при том обусловленный собственной сложной динамикой системы, а не каким-либо внешним шумовым воздействием на нее.
В диссипативных системах хаос ассоциируется с наличием в фазовом пространстве странных аттракторов – сложно устроенных фрактальных множеств, притягивающих к себе все траектории из некоторой прилегающей области – бассейна аттрактора.
Слайд 51Фундаментальные эффекты, к которым приводит нелинейность. Динамический хаос
О предмете теории
колебаний
Система уравнений Лоренца