Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объём призмы
Содержание
- 1. Объём призмы
- 2. Рассмотреть доказательство, выполнить краткую запись, сегодня можно не сдавать
- 3. Вопросы для повторения1.Что называют объёмом?2. Сформулируйте основные
- 4. Объём треугольной призмы Рассмотрим сначала треугольную призму
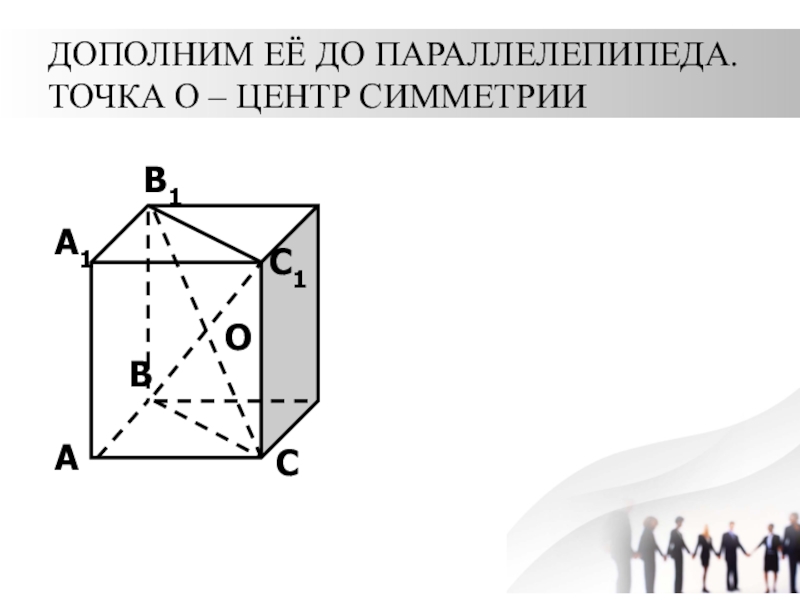
- 5. Дополним её до параллелепипеда. Точка О –
- 6. Поэтому, достроенная призма симметрична исходной
- 7. ОБЪЁМ ПАРАЛЛЕЛЕПИПЕДА РАВЕН V = SОСН ·НПлощадь
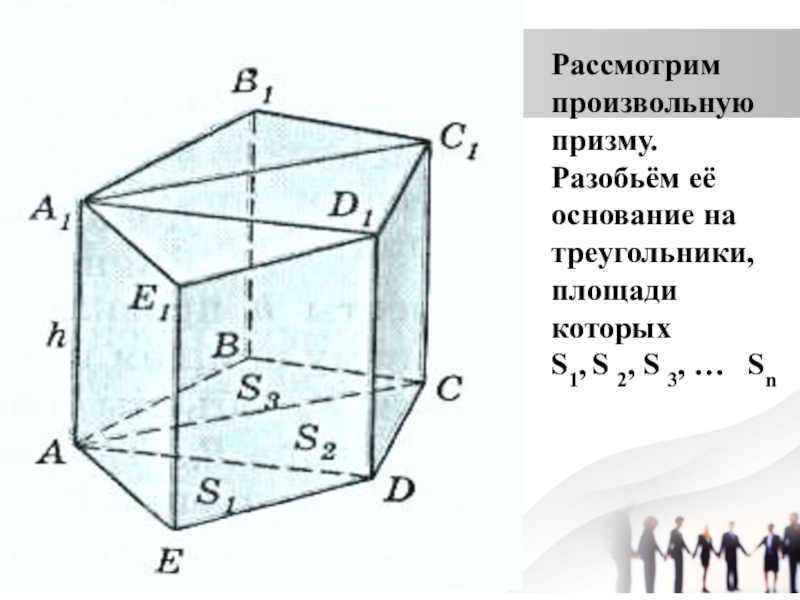
- 8. Рассмотрим произвольную призму. Разобьём её основание на
- 9. Объём данной призмы равен сумме
- 10. Вывод:Итак, объём любой призмы равен произведению площади её основания на высоту
- 11. Решить задачуНайдите объём правильной n – угольной
- 12. Вопросы1. Чему равен объём треугольной призмы ?2.
- 13. Скачать презентанцию
Рассмотреть доказательство, выполнить краткую запись, сегодня можно не сдавать
Слайды и текст этой презентации
Слайд 3Вопросы для повторения
1.Что называют объёмом?
2. Сформулируйте основные свойства объёма.
3. Чему
равен объём прямоугольного параллелепипеда?
Слайд 6 Поэтому, достроенная призма симметрична исходной относительно точки О,
следовательно имеет объём, равный объёму исходной призмы.
Таким образом,
объём построенного параллелепипеда равен удвоенному объёму данной призмы
Слайд 7ОБЪЁМ ПАРАЛЛЕЛЕПИПЕДА РАВЕН V = SОСН ·Н
Площадь его основания равна
удвоенной площади треугольника АВС, а высота равна высоте исходной призмы.
Отсюда заключаем, что объём исходной призмы равен произведению площади её основания на высоту
Слайд 8Рассмотрим произвольную призму. Разобьём её основание на треугольники, площади которых
S1, S 2, S 3, … Sn
Слайд 9Объём данной призмы равен сумме объёмов треугольных
призм, её составляющих
По доказанному объём треугольной призмы равен произведению площади
её основания на высоту. Отсюда следует, что объём исходной призмы равен:V =V1+V2 +V3+ … +Vn = S1 H +S2 H + … + SnH
= (S1 + S2 + … + Sn) H, где
S1, S2 , …, Sn – площади треугольников, а Н – высота призмы. Сумма площадей треугольников равна площади основания данной призмы. Поэтому, V = Sосн H
Слайд 11Решить задачу
Найдите объём правильной
n – угольной призмы, у которой
сторона а = 10 см , если:
1) n = 3;
2)
n = 4.Высота равна 20 см
Слайд 12Вопросы
1. Чему равен объём треугольной призмы ?
2. Чему равен объём
четырёхугольной призмы ?
3. Чему равен объём n – угольной призмы
?
