Однофакторный дисперсионный анализ ( лекционное занятие)

дисперсионном анализе

распределены нормально и имеют одинаковую, хотя и неизвестную, дисперсию
Математические

ожидания также неизвестны, но могут быть различными
Требуется: при заданном уровне значимости по выборочным средним проверить нулевую гипотезу
Н0:М (X1) = М (Х2) = ... = М(Хр)
о равенстве всех математических ожиданий

значимо или незначимо различаются выборочные средние
Казалось бы, для сравнения

нескольких средних (р > 2) можно сравнить их попарно
Однако с возрастанием числа средних возрастает и наибольшее различие между ними:
- среднее новой выборки может оказаться больше наибольшего или меньше наименьшего из средних, полученных до нового опыта
По этой причине для сравнения нескольких средних пользуются другим методом, который основан на сравнении дисперсий и поэтому назван дисперсионным анализом (в основном развит английским статистиком Р. Фишером)

установить, оказывает ли существенное влияние некоторый качественный фактор F, который

имеет р уровней F1, F2,..., Fp на изучаемую величину X.
Например, если требуется выяснить, какой вид преступлений встречается наиболее часто, то фактор F - преступление, а его уровни - виды преступлений

сравнении «факторной дисперсии», порождаемой воздействием фактора, и «остаточной дисперсии», обусловленной

случайными причинами
Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на X; в этом случае средние наблюдаемых значений на каждом уровне (групповые средние) различаются также значимо

влияет на X, а требуется выяснить, какой из уровней оказывает

наибольшее воздействие, то дополнительно производят попарное сравнение средних

однородность нескольких совокупностей (дисперсии этих совокупностей одинаковы по предположению; если

дисперсионный анализ покажет, что и математические ожидания одинаковы, то в этом смысле совокупности однородны)
Однородные же совокупности можно объединить в одну и тем самым получить о ней более полную информацию, следовательно, и более надежные выводы

нескольких факторов на нескольких постоянных или случайных уровнях и выясняют

влияние отдельных уровней и их комбинаций (многофакторный анализ)
На лекции ограничимся рассмотрением простейшего случая однофакторного анализа, когда на X воздействует только один фактор, который имеет р постоянных уровней

X воздействует фактор F, который имеет р постоянных уровней
Будем

предполагать, что число наблюдений (испытаний) на каждом уровне одинаково и равно q

pq значений хij признака X,
где i -

номер испытания (i = 1, 2, ..., p);
j - номер уровня фактора (j = 1, 2, ..., р)
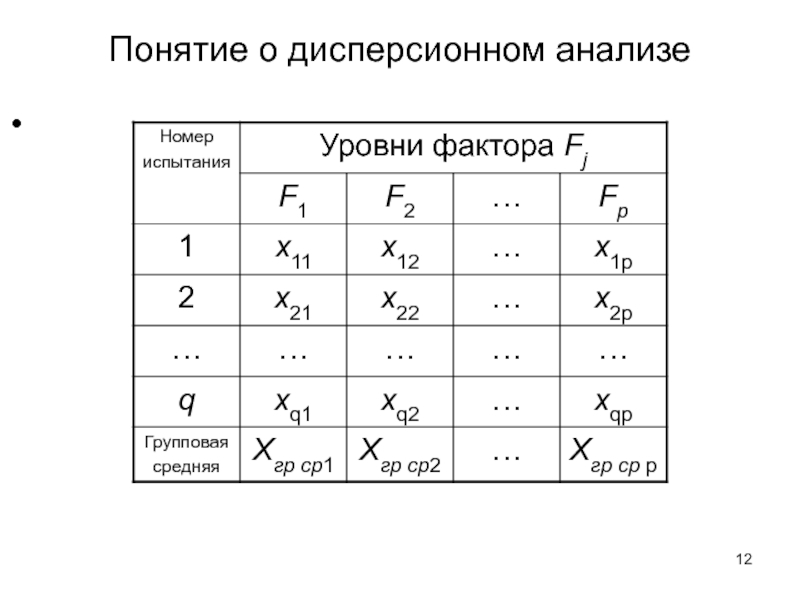
Результаты наблюдений приведены в таблице на следующем слайде

общей суммы квадратов отклонений наблюдаемых значений от общей средней х:

факторной суммы квадратов отклонений групповых средних от общей средней, которая

характеризует рассеяние «между группами»:

остаточной суммы квадратов отклонений наблюдаемых значений группы от своей групповой

средней, которая характеризует рассеяние «внутри групп»:

Sост = Sобщ – Sфакт
Элементарными преобразованиями можно

получить формулы, более удобные для расчетов:

значений признака на уровне Fj ;


это сумма

значений признака на уровне Fj

наблюдаемого значения одно и то же число С, примерно равнее

общей средней
Если уменьшенные значения уij = хij - С, то:

уменьшенных значений признака на уровне Fj;


- сумма уменьшенных

значений признака на уровне Fj

суммы на соответствующее число степеней свободы, находят факторную и остаточную

дисперсии:

и остаточной дисперсий по критерию Фишера-Снедекора
-

Если Fнабл < Fкр, различие групповых средних незначимое;
- Если Fнабл > Fкр, различие групповых средних значимое

то это свидетельствует о справедливости нулевой гипотезы о равенстве групповых

средних, поэтому дальнейшие вычисления (сравнение дисперсий с помощью критерия Фишера) излишни

числами с k знаками после запятой, то целесообразно перейти к

целым числам:
yij = 10k xij – C,
где C – примерно среднее значение чисел 10k xij
При этом факторная и остаточная дисперсии увеличатся каждая в 102k раз, но их отношение не изменится

анализа