Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОКРУЖНОСТЬ
Содержание
- 1. ОКРУЖНОСТЬ
- 2. ВПИСАННЫЕ И ЦЕНТРАЛЬНЫЕ УГЛЫУгол с вершиной в
- 3. СВОЙСТВА ВПИСАННЫх уГЛов)))Вписанный угол равен половине центрального
- 4. СВОЙСТВА ВПИСАННЫх уГЛов))Все вписанные углы, опирающиеся на
- 5. УГЛЫ МЕЖДУ ХОРДАМИ, КАСАТЕЛЬНЫМИ и СЕКУЩИМИ )Угол
- 6. Углы между хордами, касательными и секущимиУгол между
- 7. СВОЙСТВА хордБольшая из двух хорд находится ближе
- 8. СВОЙСТВА хордДлина хорды: LЕсли диаметр делит
- 9. СВОЙСТВА дуг и хордДуги, заключенные между параллельными хордами, равны.Равные дуги стягиваются равными хордами.проверь себя
- 10. Соотношения между длинами хорд, отрезков касательных и
- 11. Соотношения между длинами хорд, отрезков касательных и
- 12. Скачать презентанцию
ВПИСАННЫЕ И ЦЕНТРАЛЬНЫЕ УГЛЫУгол с вершиной в центре окружности называется её центральным углом. Центральный угол измеряется дугой, на которую он опирается.Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется
Слайды и текст этой презентации
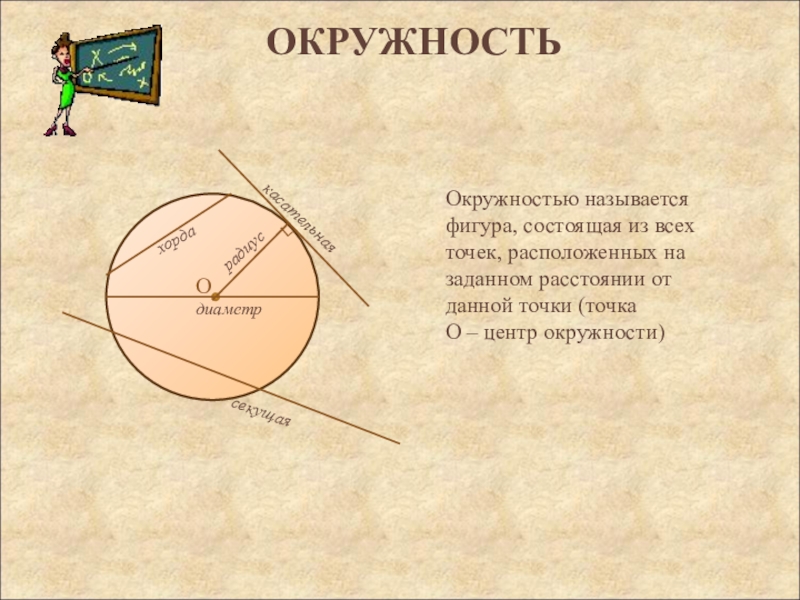
Слайд 1ОКРУЖНОСТЬ
О
диаметр
хорда
касательная
секущая
L
Окружностью называется фигура, состоящая из всех точек, расположенных на заданном
расстоянии от данной точки (точка
Слайд 2ВПИСАННЫЕ И ЦЕНТРАЛЬНЫЕ УГЛЫ
Угол с вершиной в центре окружности называется
её центральным углом.
Центральный угол измеряется дугой, на которую он
опирается.Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Вписанный угол измеряется половиной дуги, на которую он опирается.
вписанный
централь
ный
)
)
)
Слайд 3СВОЙСТВА ВПИСАННЫх уГЛов
)
)
)
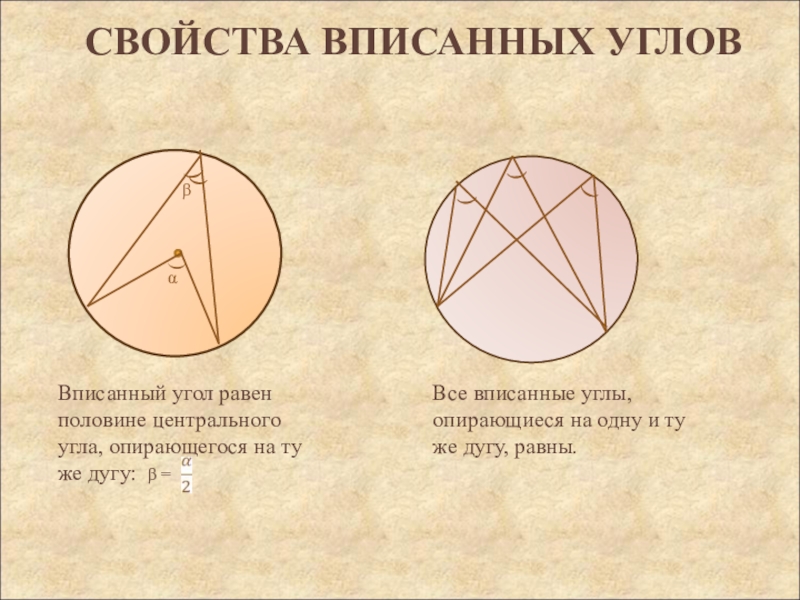
Вписанный угол равен половине центрального угла, опирающегося на
ту же дугу: β =
α
β
)
)
)
Все вписанные углы, опирающиеся
на одну и ту же дугу, равны. 
Слайд 4СВОЙСТВА ВПИСАННЫх уГЛов
)
)
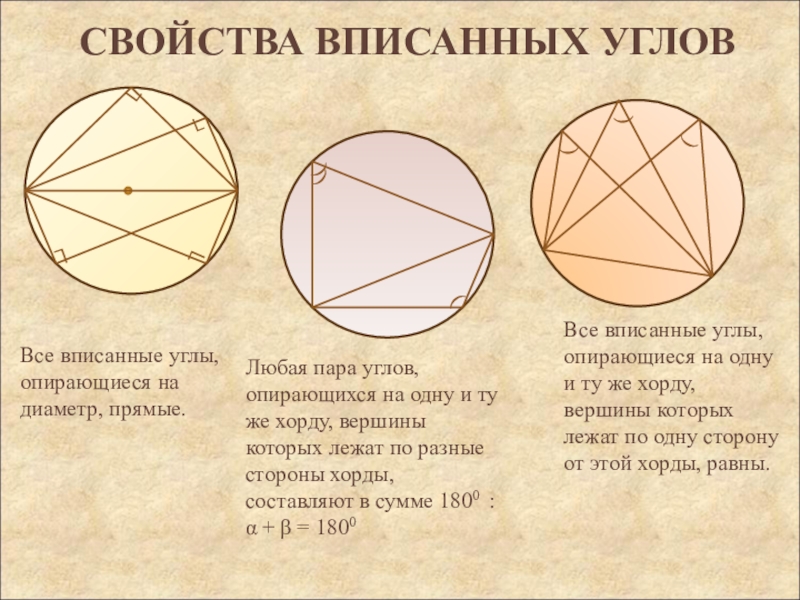
Все вписанные углы, опирающиеся на диаметр, прямые.
α
β
)
)
)
Все вписанные углы, опирающиеся на одну и ту же хорду,
вершины которых лежат по одну сторону от этой хорды, равны. L
L
L
L
)
Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 1800 : α + β = 1800
)
)
Слайд 5УГЛЫ МЕЖДУ ХОРДАМИ, КАСАТЕЛЬНЫМИ и СЕКУЩИМИ
)
Угол между пересекающими хордами
α
β
)
Угол между секущими, пересекающимися вне окружности: γ =
γ
γ =
α
β
γ
Слайд 6Углы между хордами, касательными и секущими
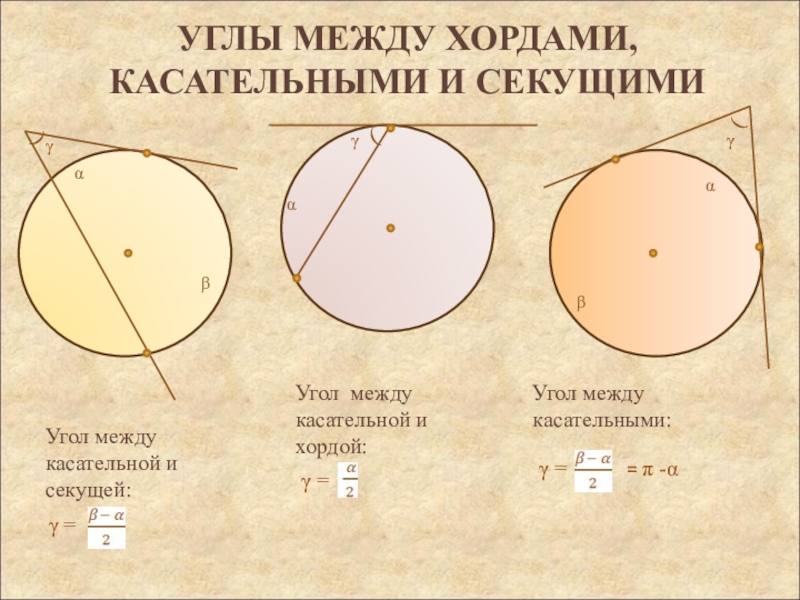
Угол между касательной и секущей:
)
)
Угол между касательными:
)
Угол между касательной и хордой:
α
αβ
β
γ
γ
γ
α
γ =
γ =
γ =
= π -α
Слайд 7СВОЙСТВА хорд
Большая из двух хорд находится ближе к центру окружности.
Наибольшая
хорда является диаметром.
L
L
L
L
Если хорды равноудалены от центра окружности, то
они равны.Если хорды равны, то они равноудалены от центра окружности.
Слайд 8СВОЙСТВА хорд
Длина хорды:
L
Если диаметр делит хорду пополам, то
он перпендикулярен ей.
Если диаметр перпендикулярен хорде, то он делит её
пополам.α
)
)
β
)
R
l
2R
l =
=
2R
проверь себя
Слайд 9СВОЙСТВА дуг и хорд
Дуги, заключенные между параллельными хордами, равны.
Равные дуги
стягиваются равными хордами.
проверь себя
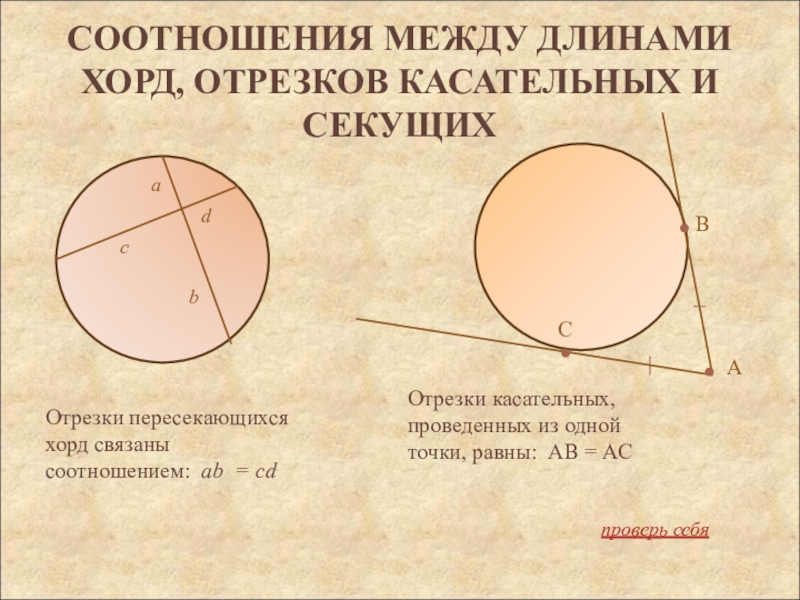
Слайд 10Соотношения между длинами хорд, отрезков касательных и секущих
Отрезки пересекающихся хорд
связаны соотношением: ab = cd
Отрезки касательных, проведенных из одной точки,
равны: АВ = АС a
b
c
d
A
B
C
проверь себя
Слайд 11Соотношения между длинами хорд, отрезков касательных и секущих
Квадрат отрезка касательной
равен произведению отрезков секущей, проведенной из той же точки:
Произведения
отрезков секущих, проведенных из одной точки, равны: A
B
C
B
A
C
D
D
K
AB
AC = AD
проверь себя
