Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Окружность (по материалам открытого банка задач ОГЭ по математике) 201 9
Содержание
- 1. Окружность (по материалам открытого банка задач ОГЭ по математике) 201 9
- 2. Повторение теорииКасательная к окружностиПрямая, имеющая с окружностью
- 3. Отрезки касательных к окружности, проведенные из одной
- 4. Центральный уголВписанный уголУгол с вершиной в центре
- 5. Центральный уголВписанный уголВеличина дуги окружности равна величине
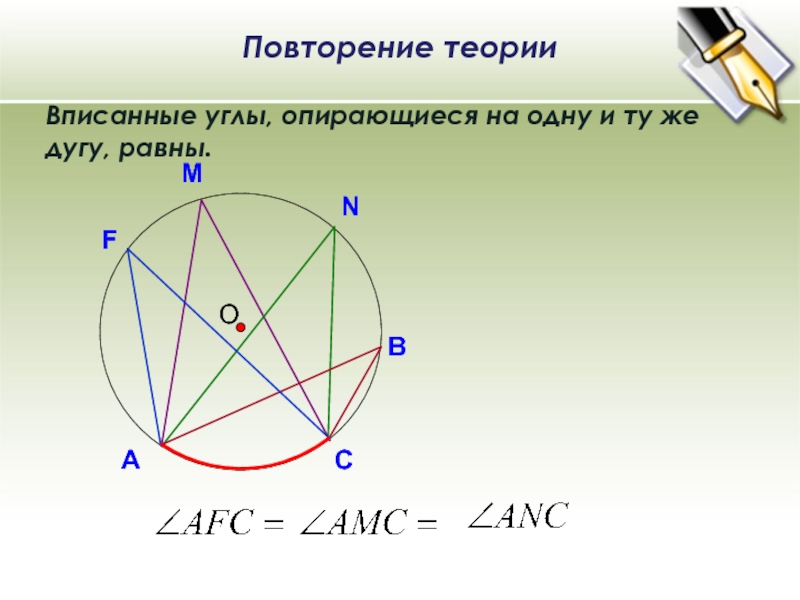
- 6. ОВписанные углы, опирающиеся на одну и ту же дугу, равны.ВNMПовторение теории
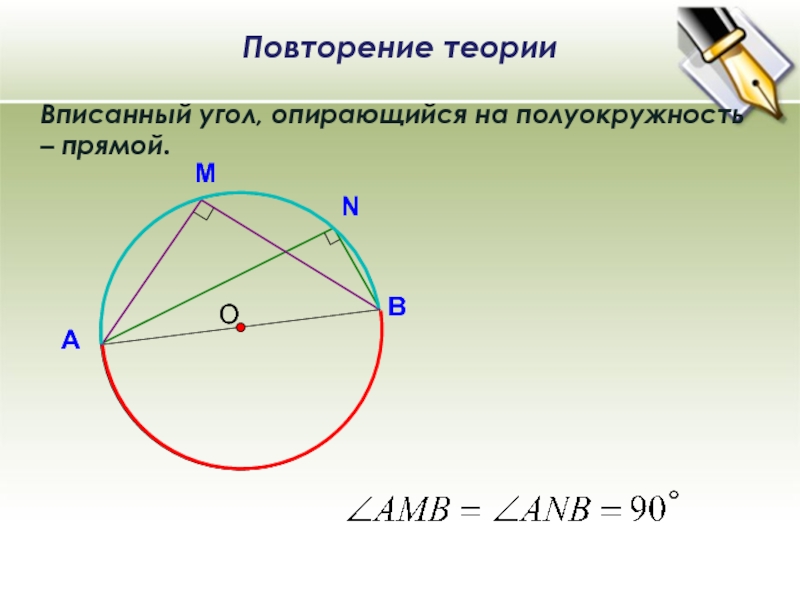
- 7. ОВписанный угол, опирающийся на полуокружность – прямой.ВА°Повторение теории
- 8. Повторение теорииУгол между касательной и хордой равен
- 9. BАCDEТеорема об отрезках пересекающихся хордЕсли две хорды
- 10. BОАЕсли из одной точки проведены к окружности
- 11. В любом вписанном четырёхугольнике сумма его противоположных
- 12. В любом описанном четырёхугольнике суммы противоположных сторон
- 13. Какие из следующих утверждений верны?1) Для точки,
- 14. № 1. Радиус окружности, вписанной в трапецию, равен 42. Найдите высоту этой трапеции. Ответ: 84
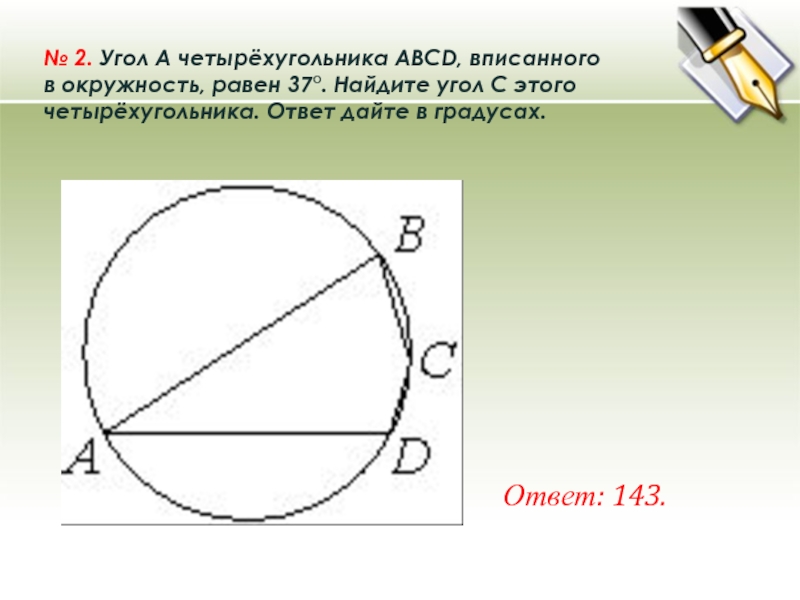
- 15. № 2. Угол A четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.Ответ: 143.
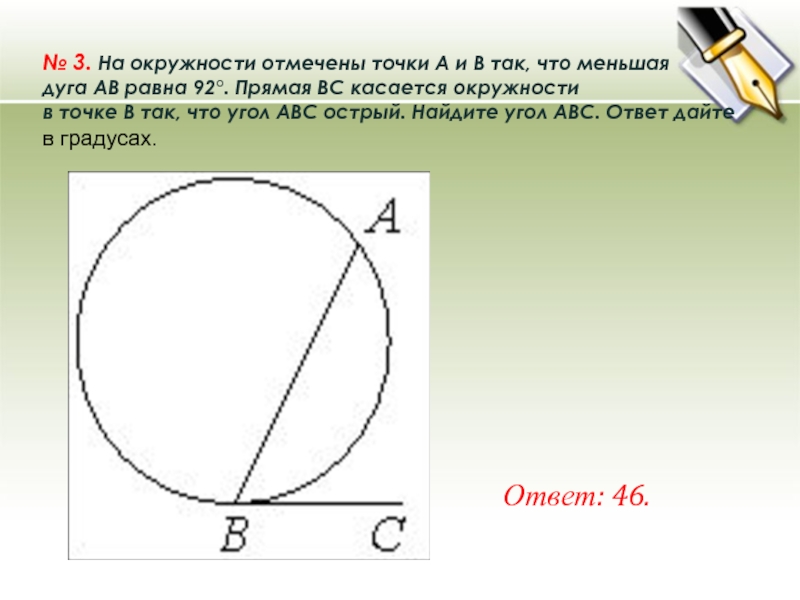
- 16. № 3. На окружности отмечены точки A и B так, что меньшая
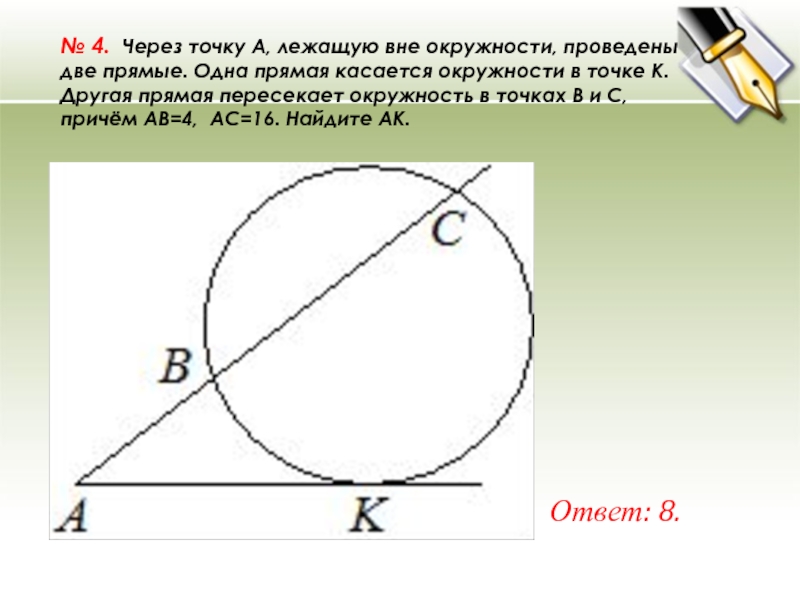
- 17. № 4. Через точку A, лежащую вне окружности, проведены
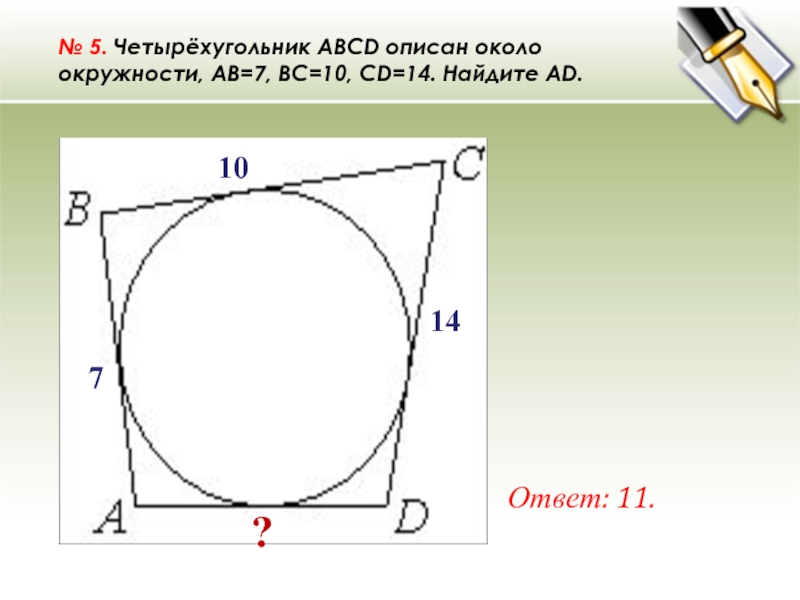
- 18. № 5. Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.Ответ: 11.?14107
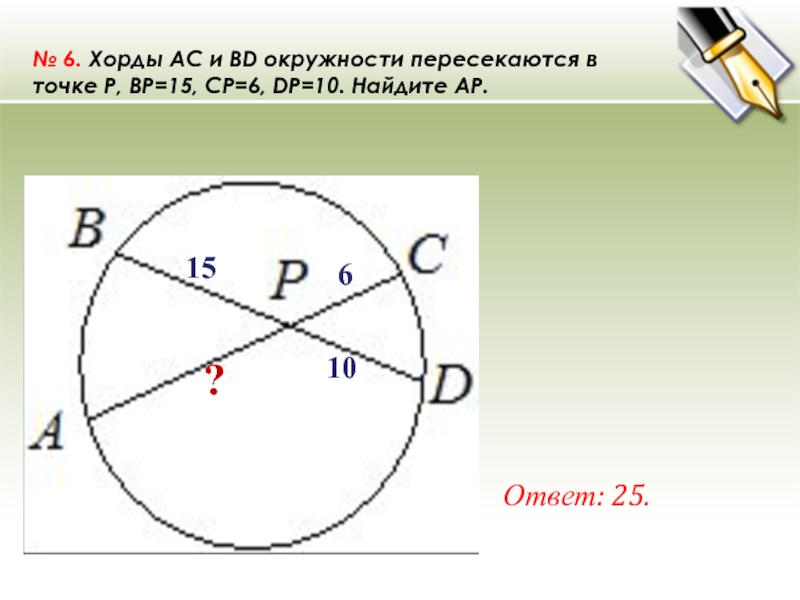
- 19. № 6. Хорды AC и BD окружности пересекаются в точке P, BP=15, CP=6, DP=10. Найдите AP.Ответ: 25.?10615
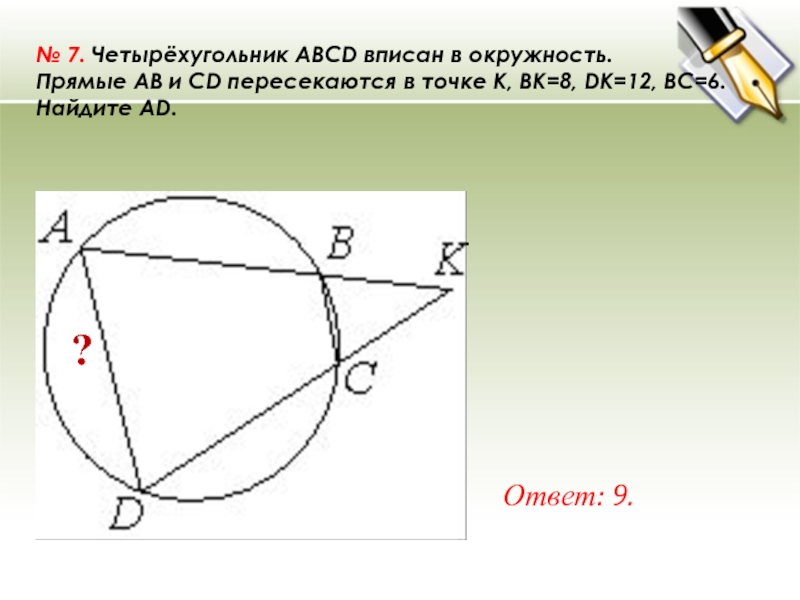
- 20. № 7. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.Ответ: 9.?
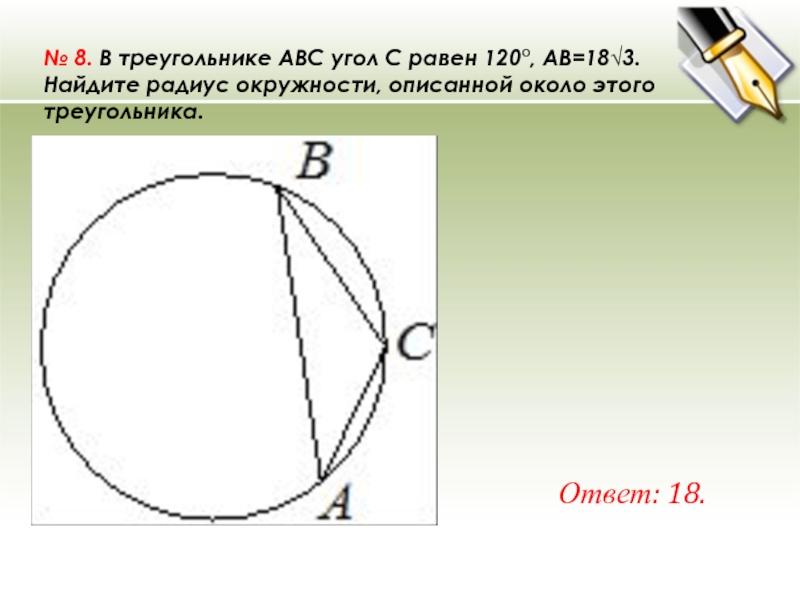
- 21. № 8. В треугольнике ABC угол C равен 120°, AB=18√3. Найдите радиус окружности, описанной около этого треугольника.Ответ: 18.
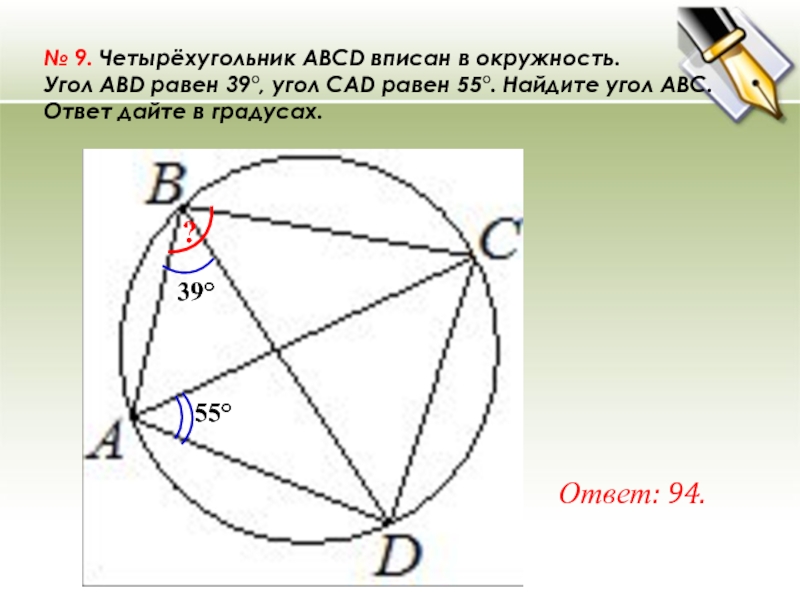
- 22. № 9. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах.Ответ: 94.39°55°?
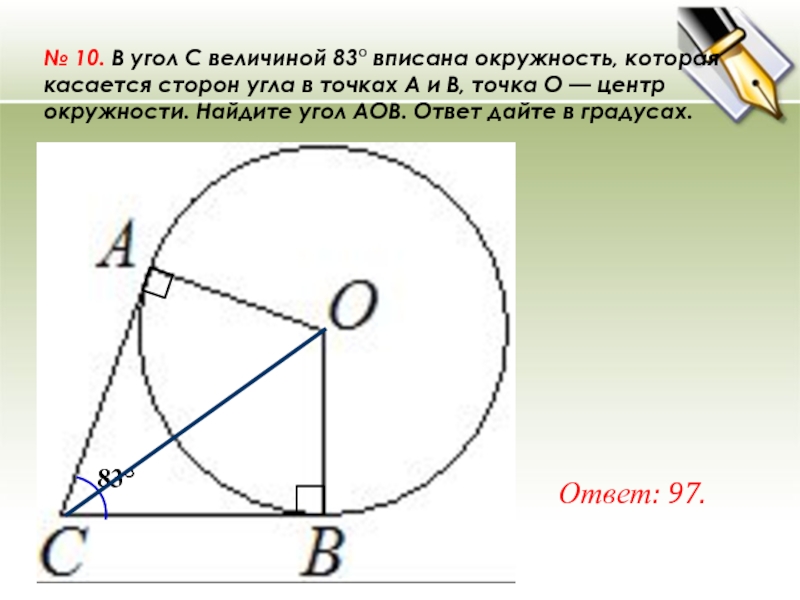
- 23. № 10. В угол C величиной 83° вписана окружность, которая касается сторон
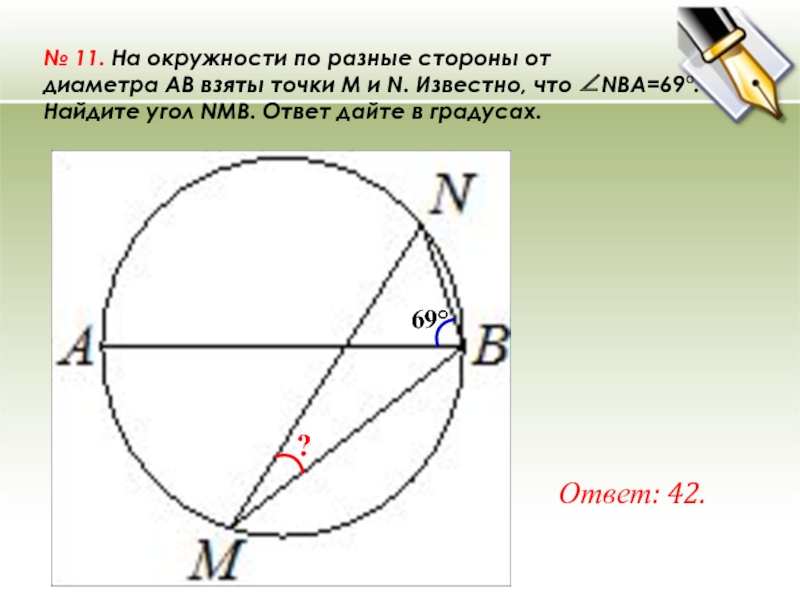
- 24. № 11. На окружности по разные стороны от
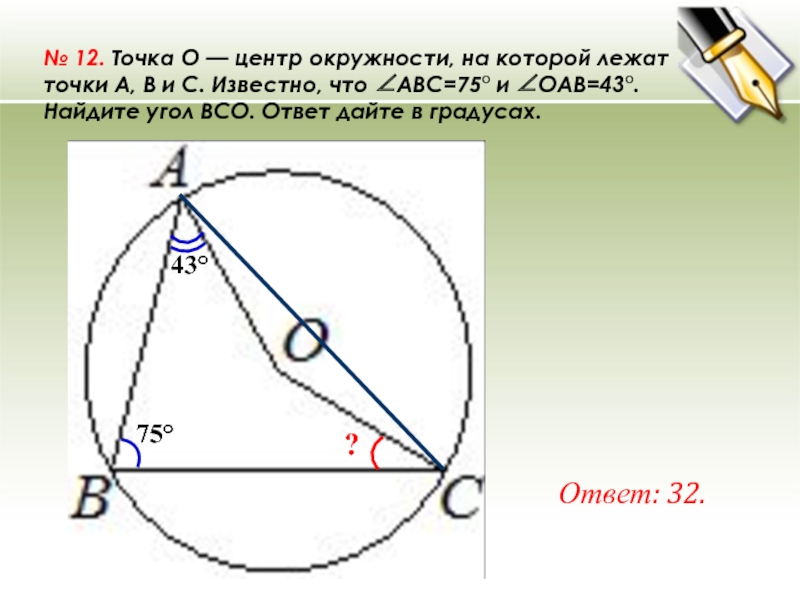
- 25. № 12. Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=75° и ∠OAB=43°. Найдите угол BCO. Ответ дайте в градусах.Ответ: 32.43°?75°
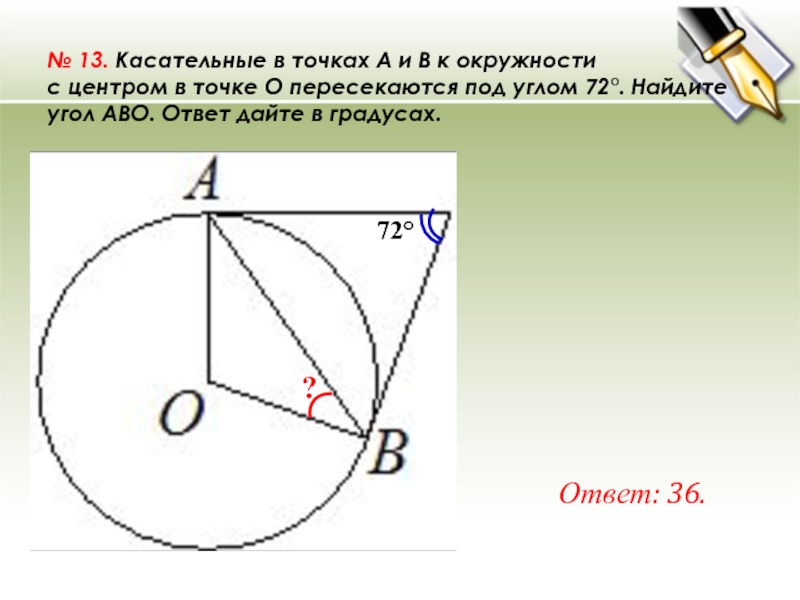
- 26. № 13. Касательные в точках A и B к окружности с центром
- 27. № 14. Окружность с центром в точке O описана около
- 28. № 15. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах.Ответ: 53.81°?134°
- 29. № 16. Треугольник ABC вписан в окружность с центром в
- 30. № 17. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.Ответ: 33.?114°
- 31. № 18. Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах.Ответ: 72.?54°
- 32. № 19. Центр окружности, описанной около треугольника ABC, лежит
- 33. № 20. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32..Ответ: 24.?202032
- 34. № 21. Периметр треугольника равен 50, одна из
- 35. Скачать презентанцию
Повторение теорииКасательная к окружностиПрямая, имеющая с окружностью единственную общую точку, называется касательной к окружности. Если прямая а, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая а-касательная к окружности.Касательная
Слайды и текст этой презентации
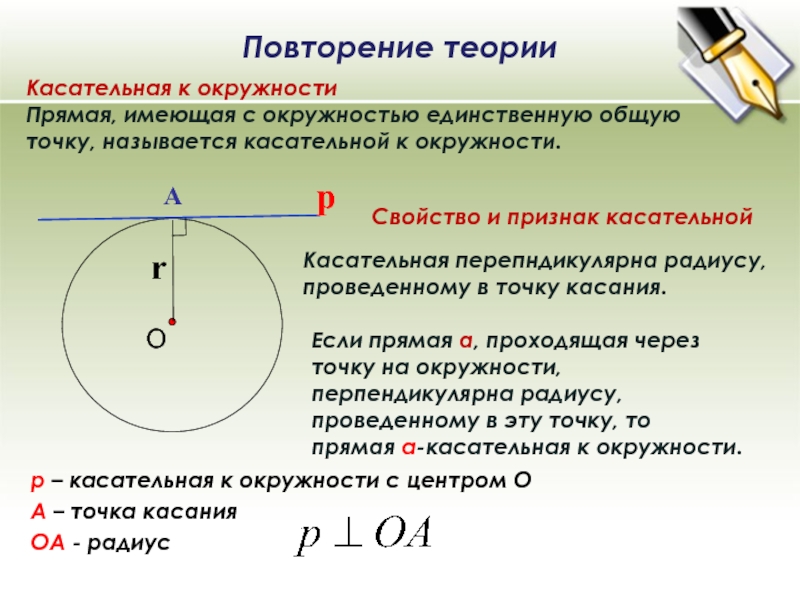
Слайд 2Повторение теории
Касательная к окружности
Прямая, имеющая с окружностью единственную общую точку,
называется касательной к окружности.
Если прямая а, проходящая через точку на
окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая а-касательная к окружности.Касательная перепндикулярна радиусу, проведенному в точку касания.
р
А
р – касательная к окружности с центром О
А – точка касания
OА - радиус
Свойство и признак касательной
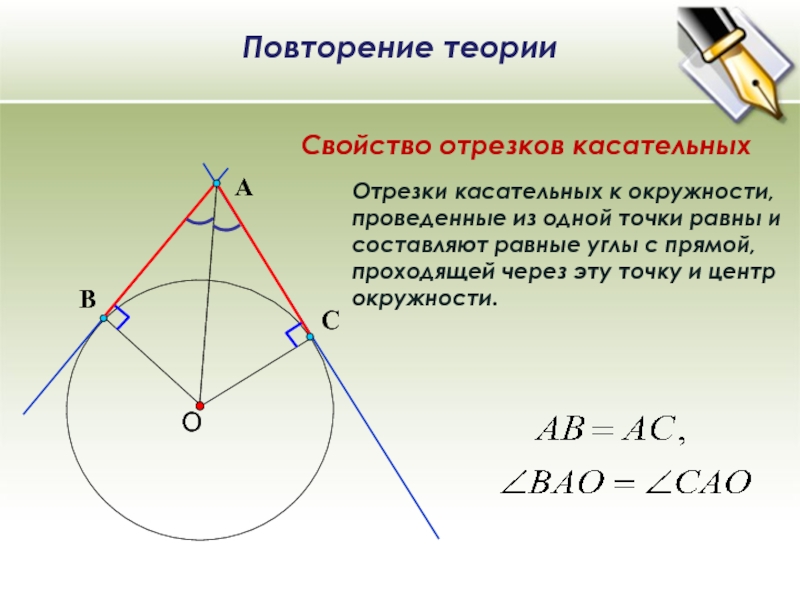
Слайд 3Отрезки касательных к окружности, проведенные из одной точки равны и
составляют равные углы с прямой, проходящей через эту точку и
центр окружности.Свойство отрезков касательных
Повторение теории
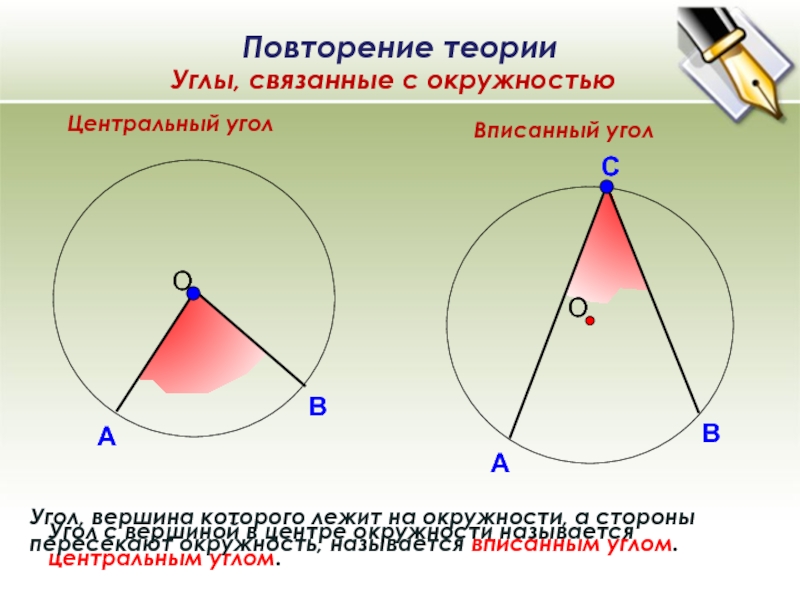
Слайд 4Центральный угол
Вписанный угол
Угол с вершиной в центре окружности называется центральным
углом.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность,
называется вписанным углом.Углы, связанные с окружностью
Повторение теории
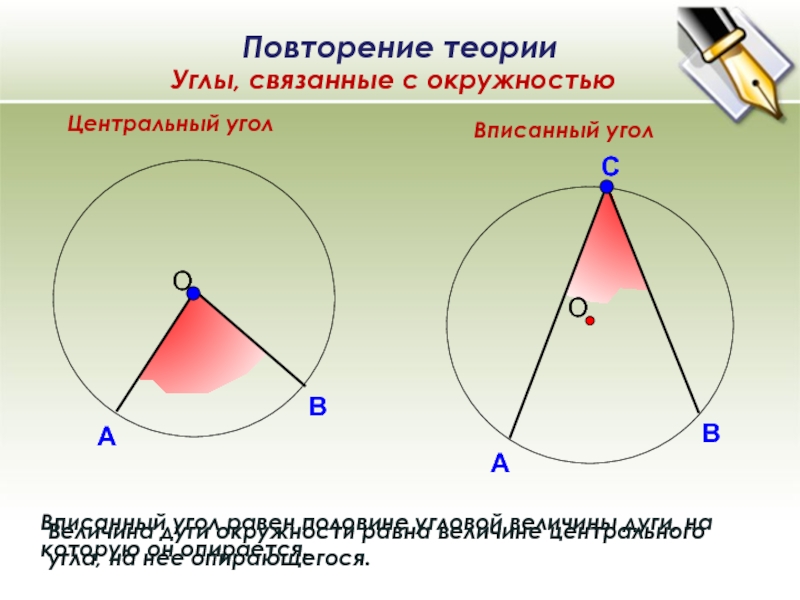
Слайд 5Центральный угол
Вписанный угол
Величина дуги окружности равна величине центрального угла, на
нее опирающегося.
Вписанный угол равен половине угловой величины дуги, на которую
он опирается.Углы, связанные с окружностью
Повторение теории
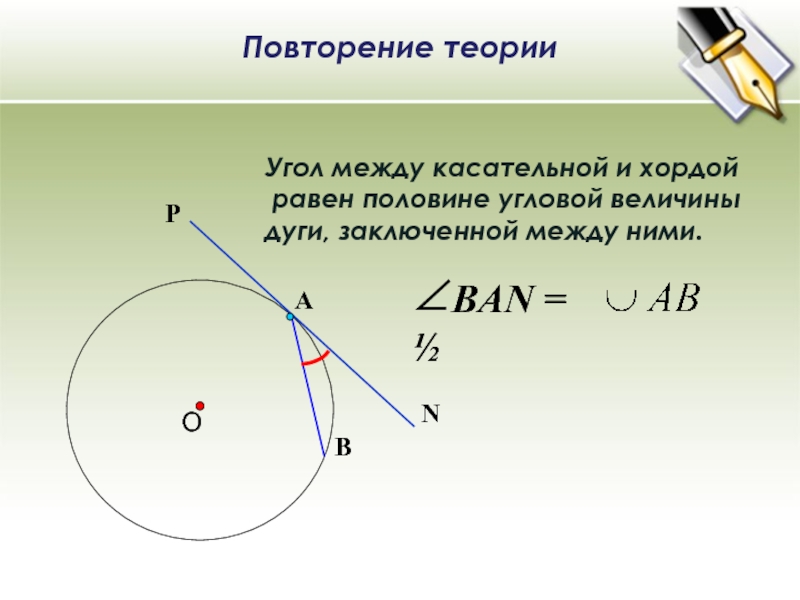
Слайд 8Повторение теории
Угол между касательной и хордой
равен половине угловой величины
дуги, заключенной между ними.
∠BAN = ½
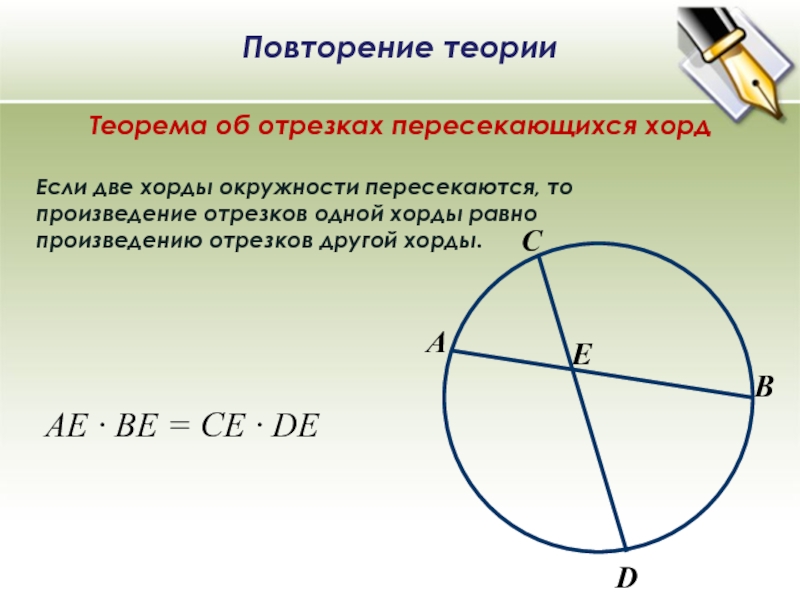
Слайд 9B
А
C
D
E
Теорема об отрезках пересекающихся хорд
Если две хорды окружности пересекаются, то
произведение
отрезков одной хорды равно
произведению отрезков другой хорды.
АЕ ∙ ВЕ =
СЕ ∙ DEПовторение теории
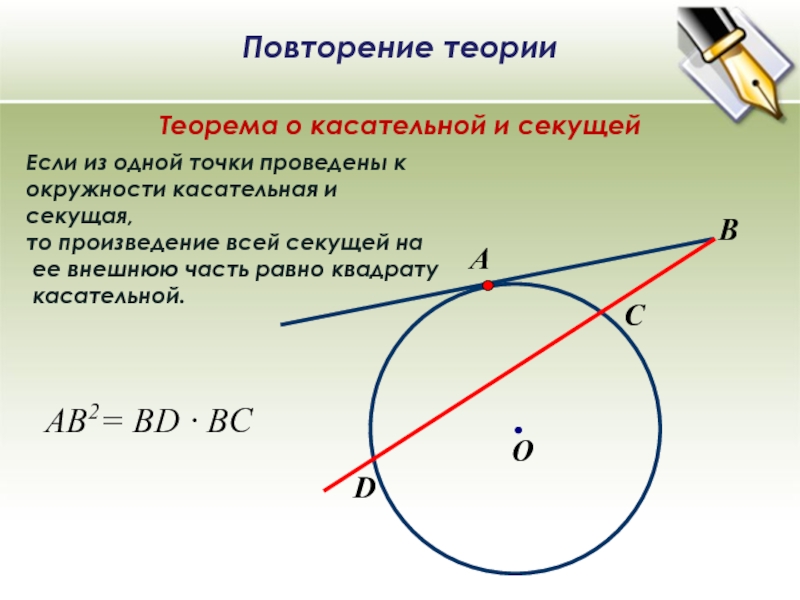
Слайд 10B
О
А
Если из одной точки проведены к
окружности касательная и секущая,
то произведение всей секущей на
ее внешнюю часть равно квадрату
касательной.C
D
AB2= BD ∙ ВC
Повторение теории
Теорема о касательной и секущей
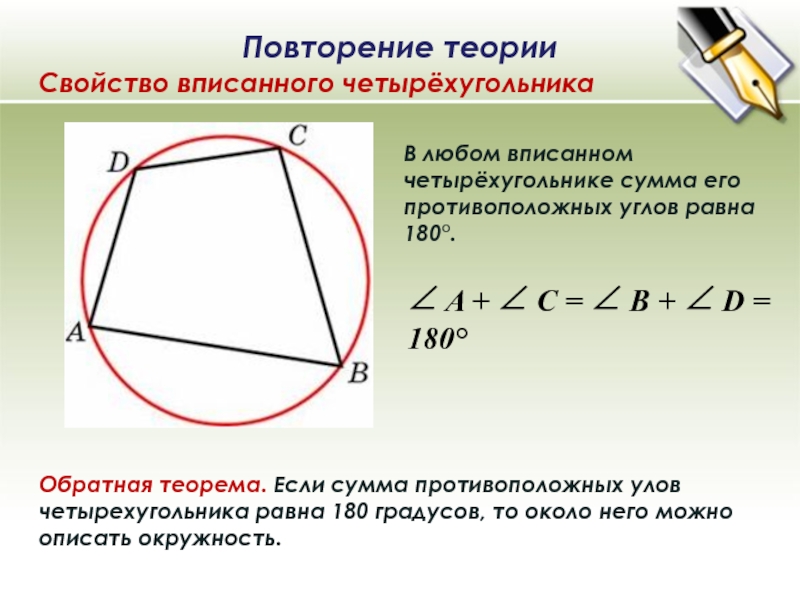
Слайд 11В любом вписанном четырёхугольнике сумма его противоположных углов равна 180°.
Обратная
теорема. Если сумма противоположных улов четырехугольника равна 180 градусов, то
около него можно описать окружность.∠ A + ∠ C = ∠ B + ∠ D = 180°
Повторение теории
Свойство вписанного четырёхугольника
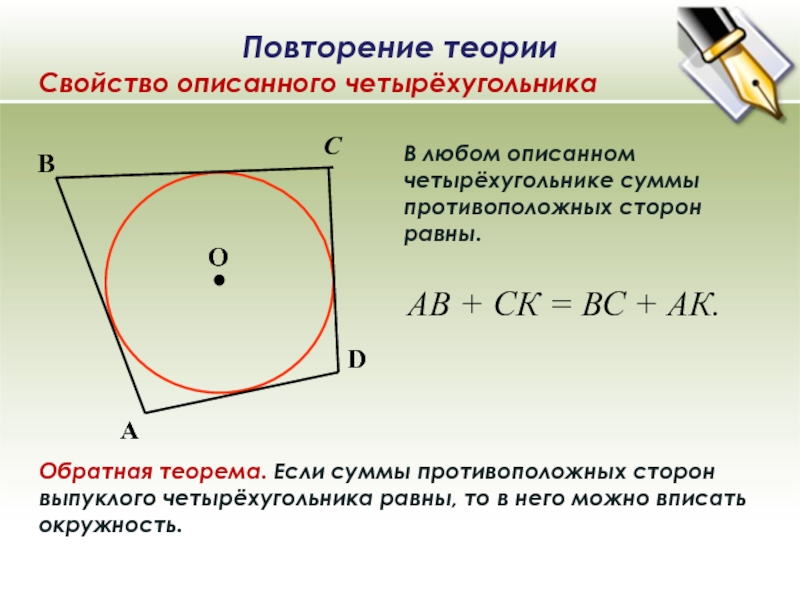
Слайд 12В любом описанном четырёхугольнике суммы противоположных сторон равны.
Обратная теорема.
Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него
можно вписать окружность.АВ + СК = ВС + АК.
Повторение теории
Свойство описанного четырёхугольника
Слайд 13Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности,
расстояние до центра окружности равно радиусу.
2) Если радиус окружности равен
3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность не пересекаются.3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
4) Около всякого треугольника можно описать не более одной окружности.
5) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
Ответ: 1, 3, 4, 6, 8, 9 .
6) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
7) Около любого ромба можно описать окружность.
8) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
9) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
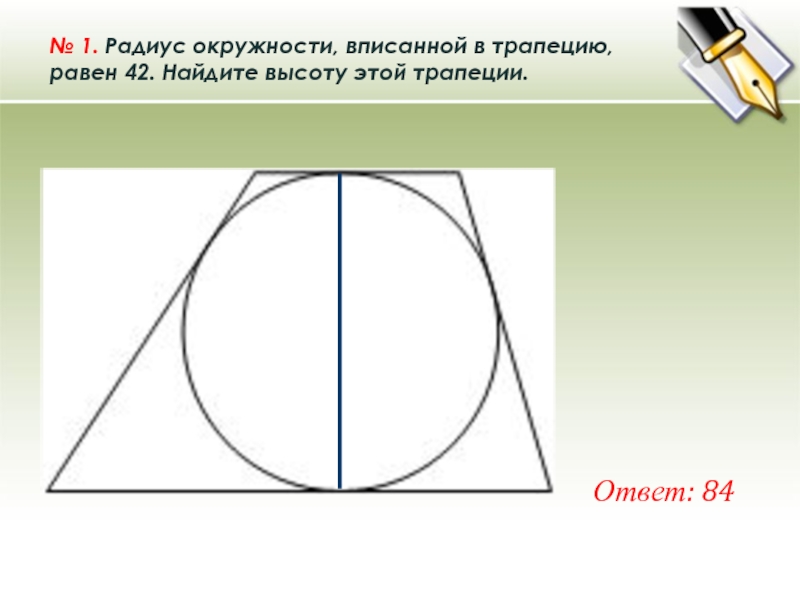
Слайд 14№ 1. Радиус окружности, вписанной в трапецию, равен 42. Найдите
высоту этой трапеции.
Ответ: 84
Слайд 15№ 2. Угол A четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол C этого четырёхугольника. Ответ дайте
в градусах.
Ответ: 143.
Слайд 16№ 3. На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в
точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Ответ: 46.
Слайд 17№ 4. Через точку A, лежащую вне окружности, проведены
две прямые. Одна
прямая касается окружности в точке K.
Другая прямая пересекает окружность в точках B и C, причём AB=4,
AC=16. Найдите AK.Ответ: 8.
Слайд 18№ 5. Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.
Ответ: 11.
?
14
10
7
Слайд 19№ 6. Хорды AC и BD окружности пересекаются в точке P, BP=15, CP=6, DP=10. Найдите AP.
Ответ: 25.
?
10
6
15
Слайд 20№ 7. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
Ответ: 9.
?
Слайд 21№ 8. В треугольнике ABC угол C равен 120°, AB=18√3.
Найдите радиус окружности, описанной около этого треугольника.
Ответ:
Слайд 22№ 9. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте
в градусах.
Ответ: 94.
39°
55°
?
Слайд 23№ 10. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B,
точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.
Ответ: 97.
83°
Слайд 24№ 11. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно,
что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
Ответ: 42.
69°
?
Слайд 25№ 12. Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=75° и ∠OAB=43°. Найдите угол BCO.
Ответ дайте в градусах.
Ответ: 32.
43°
?
75°
Слайд 26№ 13. Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 72°.
Найдите угол ABO. Ответ дайте в градусах.
Ответ: 36.
72°
?
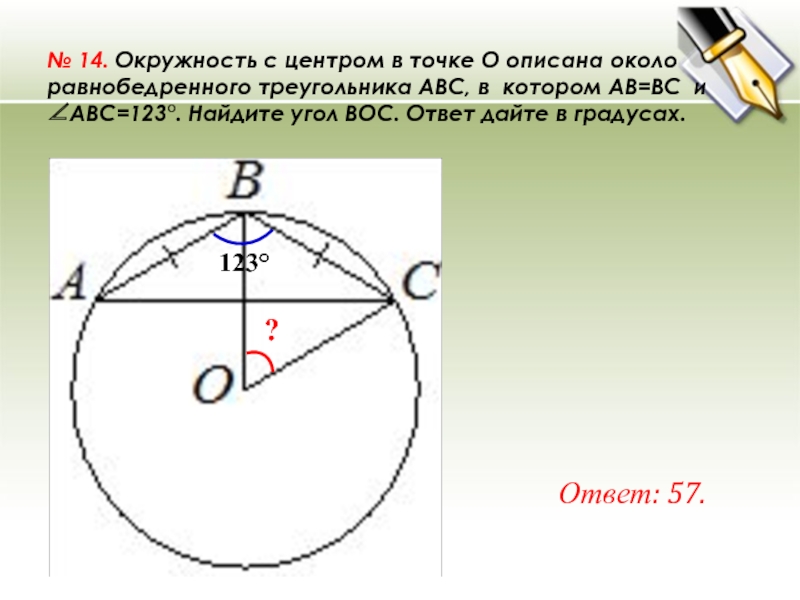
Слайд 27№ 14. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в
котором AB=BC и ∠ABC=123°. Найдите угол BOC. Ответ дайте в градусах.
Ответ: 57.
123°
?
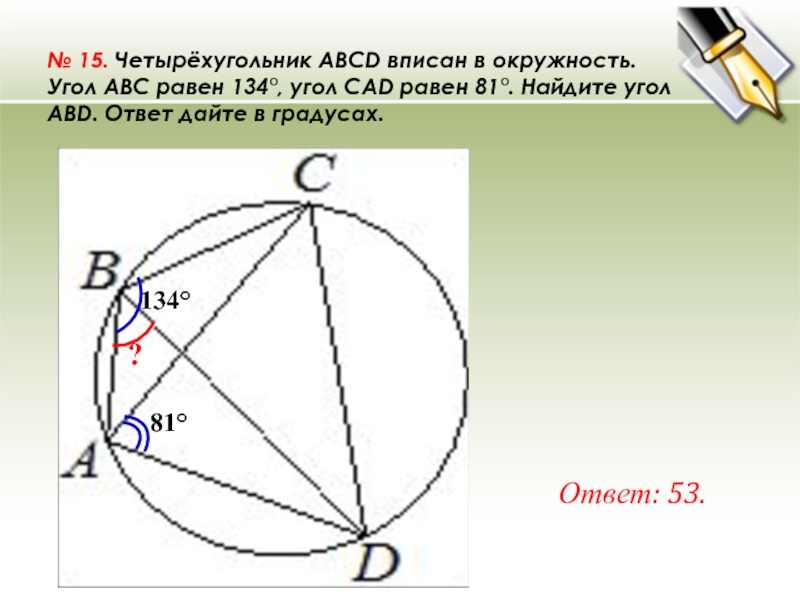
Слайд 28№ 15. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол
ABD. Ответ дайте
в градусах.
Ответ: 53.
81°
?
134°
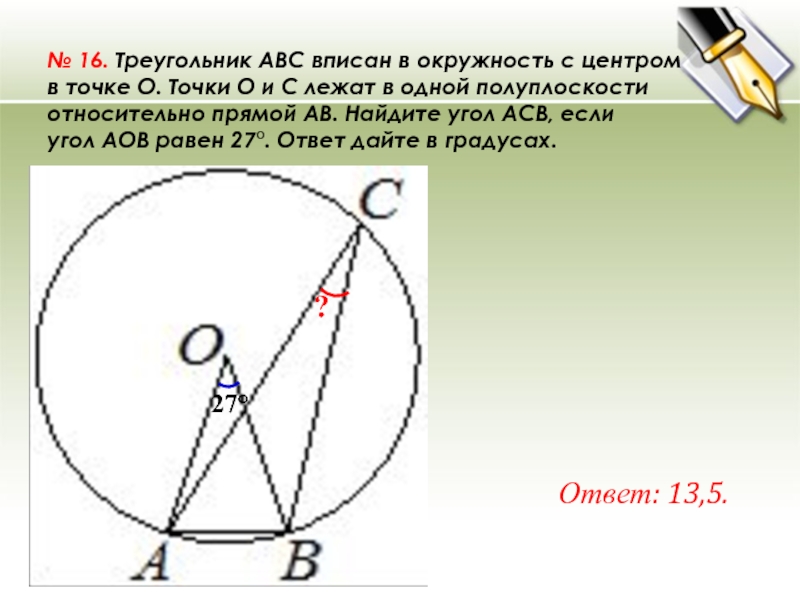
Слайд 29№ 16. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной
полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 27°. Ответ дайте в
градусах.Ответ: 13,5.
?
27°
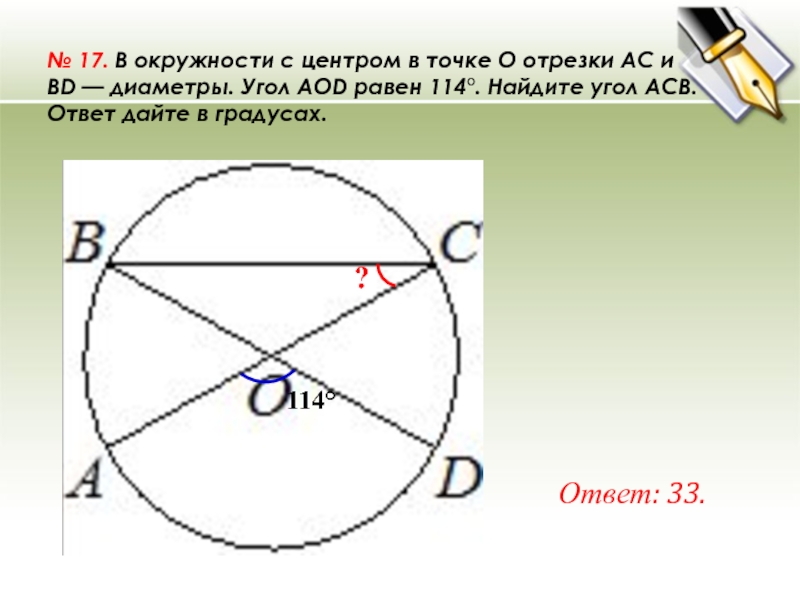
Слайд 30№ 17. В окружности с центром в точке O отрезки AC и
BD — диаметры. Угол AOD равен 114°. Найдите угол ACB.
Ответ дайте в градусах.
Ответ: 33.
?
114°
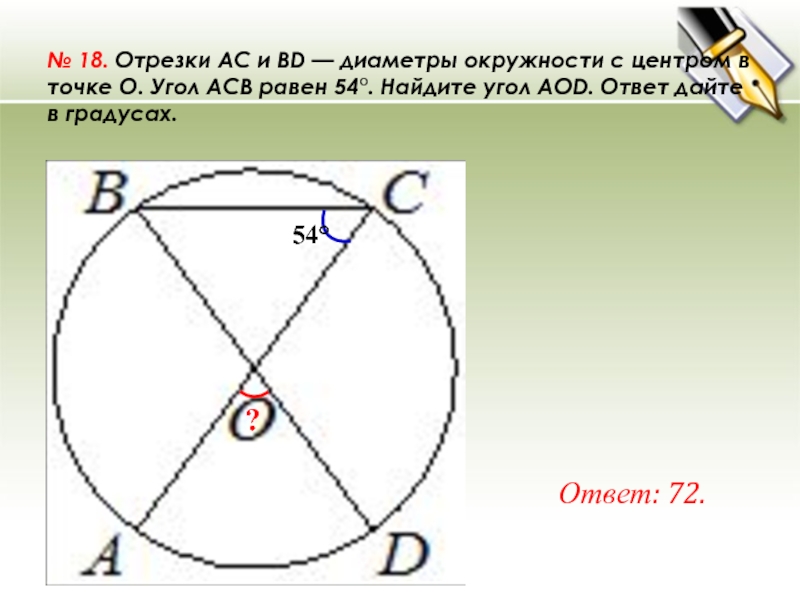
Слайд 31№ 18. Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD.
Ответ дайте в градусах.
Ответ: 72.
?
54°
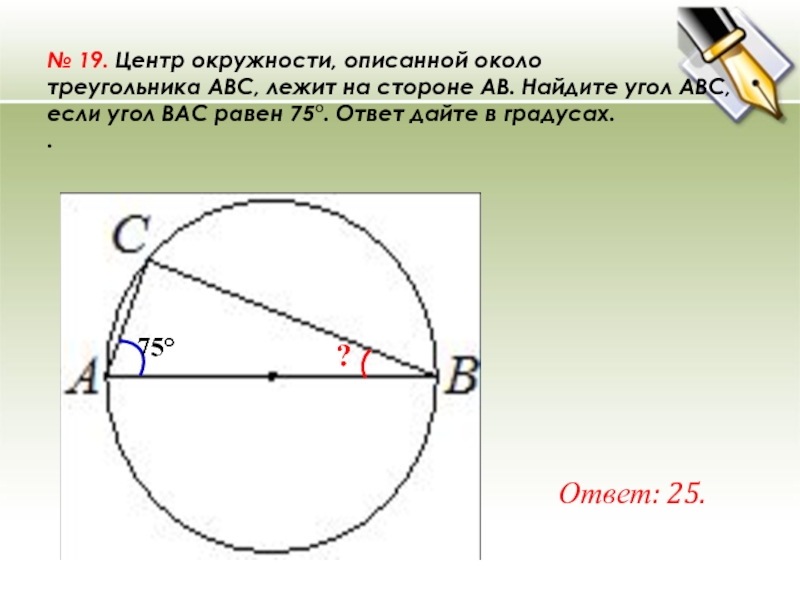
Слайд 32№ 19. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите
угол ABC, если угол BAC равен 75°. Ответ дайте в градусах.
.
Ответ: 25.
?
75°
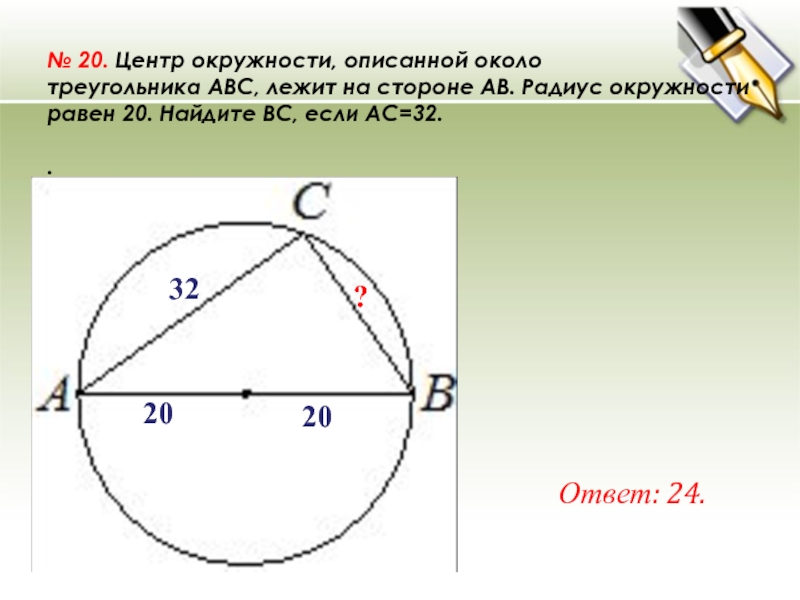
Слайд 33№ 20. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус
окружности равен 20. Найдите BC, если AC=32.
.
Ответ: 24.
?
20
20
32
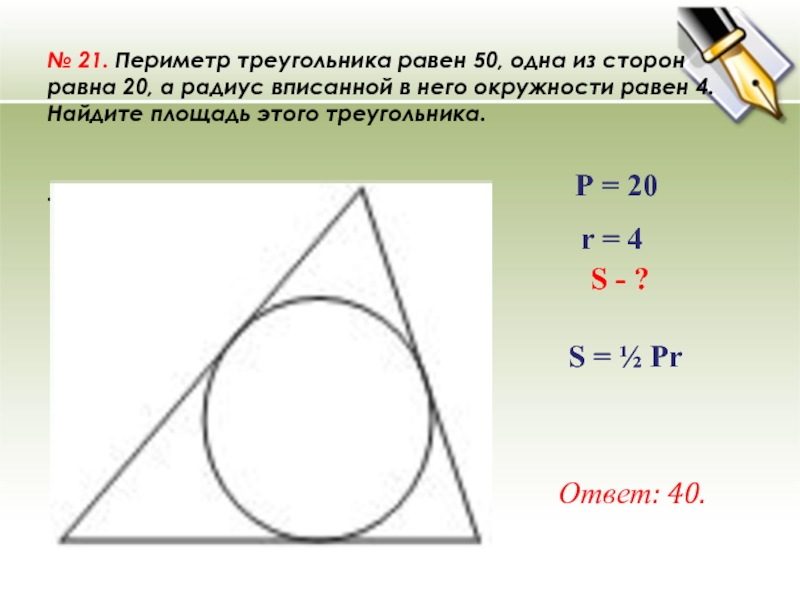
Слайд 34№ 21. Периметр треугольника равен 50, одна из сторон равна 20, а
радиус вписанной в него окружности равен 4. Найдите площадь этого
треугольника..
Ответ: 40.
S - ?
Р = 20
r = 4
S = ½ Pr
