Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приложения определенного интеграла Площади плоских фигур, заданных в
Содержание
- 1. Приложения определенного интеграла Площади плоских фигур, заданных в
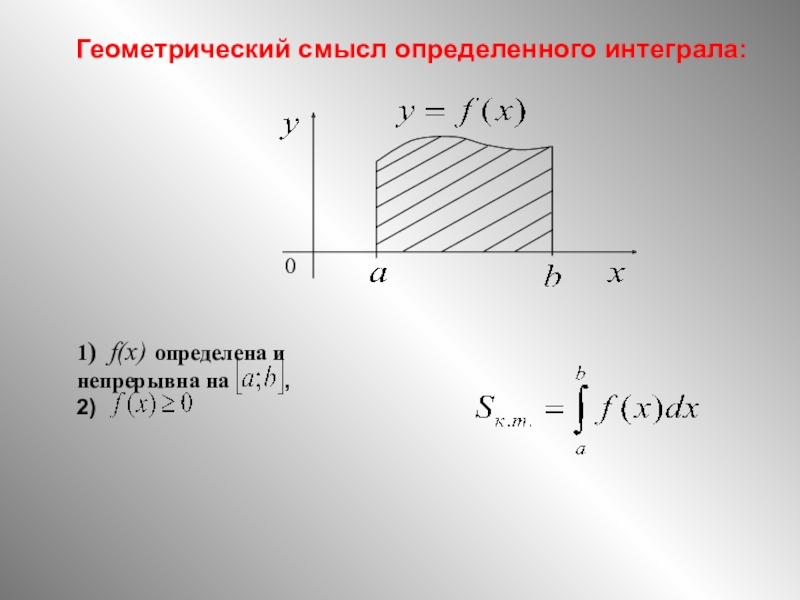
- 2. Геометрический смысл определенного интеграла:
- 3. Вычисление площадей при параметрическом задании контура 1.Пусть
- 4. Вычисление площадей при параметрическом задании контура Кривая
- 5. Слайд 5
- 6. Слайд 6
- 7. Пример. Вычислить площадь фигуры, ограниченной линиями, заданными
- 8. 2. Вычисление площадей в полярной системе координатПусть
- 9. Слайд 9
- 10. Вычисление площадей в полярной системе координат
- 11. Слайд 11
- 12. Слайд 12
- 13. Написать интеграл, выражающий площадь фигуры1.
- 14. Написать интеграл, выражающий площадь фигуры
- 15. Написать интеграл, выражающий площадь фигуры3.0
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Приложения определенного интеграла
Площади плоских фигур, заданных в параметрическом виде
и
в полярных координатах
Слайд 3Вычисление площадей
при параметрическом задании контура
1.
Пусть кривая AB: у
=f (x), где f (х) неотрицательна на отрезке [a; b],
задана в параметрической формегде функция х = φ(t) монотонна на отрезке [α; β], причем φ(α) = а, φ(β) = b,
и имеет на этом отрезке непрерывную производную.
Тогда по формуле замены переменной под знаком определенного интеграла получаем:
Слайд 4Вычисление площадей
при параметрическом задании контура
Кривая замкнутая,
обход против часовой
стрелки:
точка А - начало обхода (при t = α),
точка В
- конец обхода (при t = β)и возврат в точку А, то
2.
3.
В частности, если фигура ограничена замкнутой кривой, заданной в параметрической форме: x=x(t), y=y(t), 0 ≤t≤ T, то
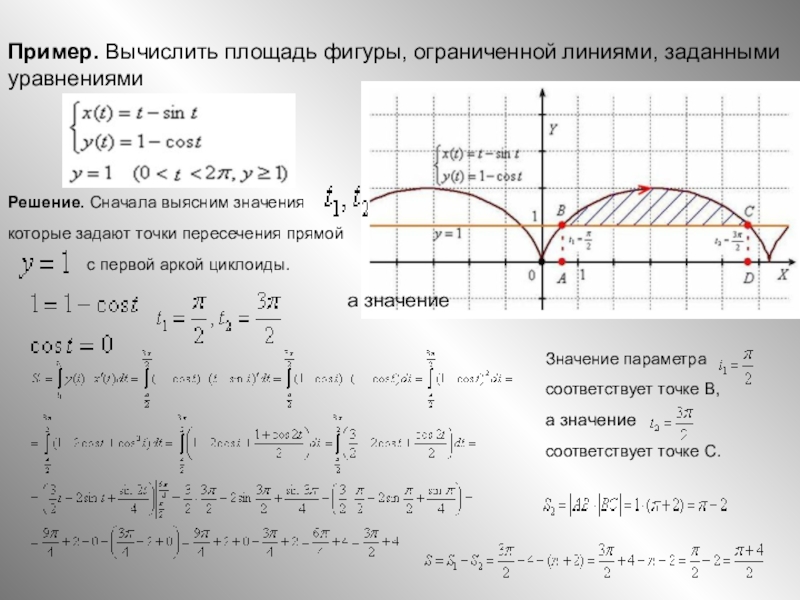
Слайд 7Пример. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями
Решение.
Сначала выясним значения
которые задают точки пересечения прямой
с первой аркой циклоиды.
Значение параметра
соответствует точке В,
а значение
соответствует точке С.
а значение
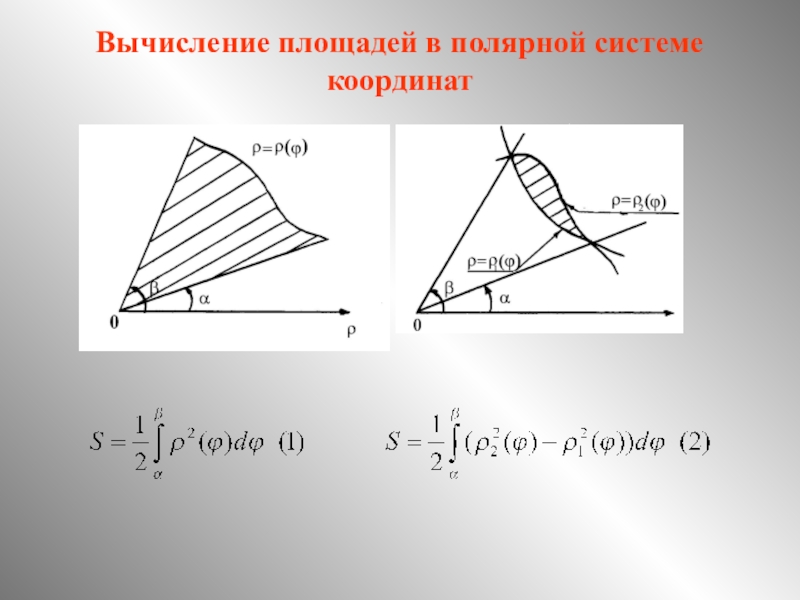
Слайд 82. Вычисление площадей в полярной системе координат
Пусть кривая АВ задана
в полярных координатах уравнением ρ=ρ(φ), α ≤ φ ≤
β. Причем функция ρ=ρ(φ ) непрерывна и неотрицательна на отрезке [а,b]. Плоскую фигуру, ограниченную кривой АВ и двумя полярными радиусами, составляющими с полярной осью углы α и β называют криволинейным сектором.Площадь S криволинейного сектора может быть вычислена по формуле