Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Олимпиадные задачи
Содержание
- 1. Олимпиадные задачи
- 2. Задача «Возрастающая подпоследовательность» № 613
- 3. Пример
- 4. Решение
- 5. Детали реализации
- 6. Сдать можно как задачу №613http://informatics.mccme.ru/mod/statements/view3.php?chapterid=613#1
- 7. Задача «Таблица» № 1150
- 8. Слайд 8
- 9. Первый способ
- 10. Второй способС диагоналями. Нужен, чтобы хранить не
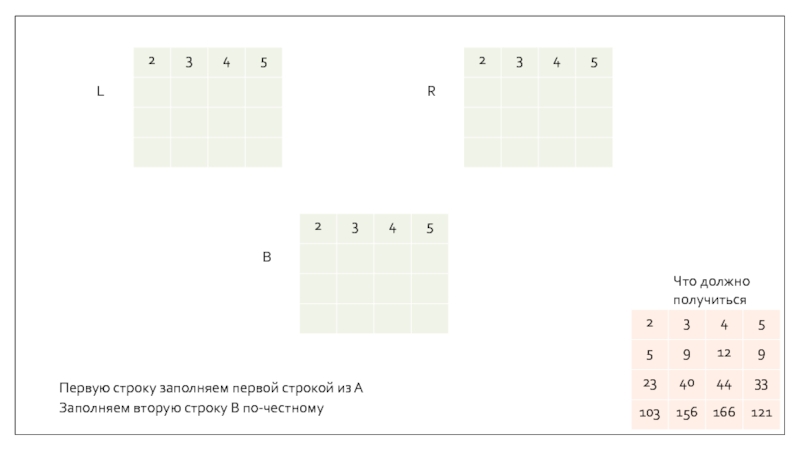
- 11. LRBЧто должно получитьсяПервую строку заполняем первой строкой из АЗаполняем вторую строку B по-честному
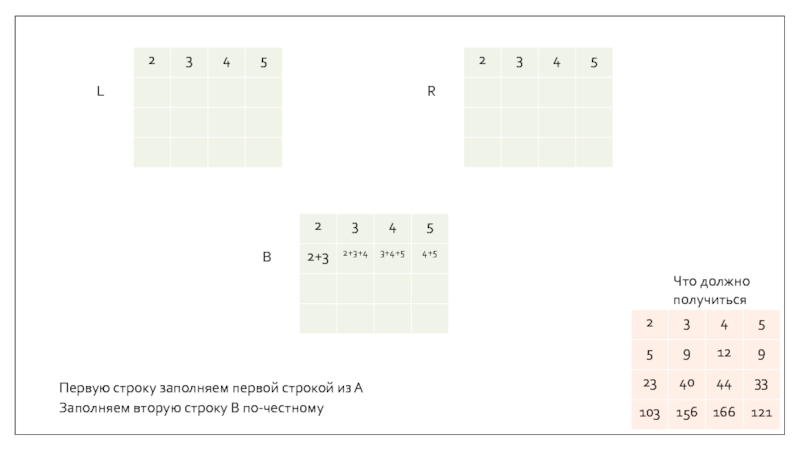
- 12. LRBЧто должно получитьсяПервую строку заполняем первой строкой из АЗаполняем вторую строку B по-честному
- 13. LRBЧто должно получитьсяТеперь можно и третью строку
- 14. LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] +
- 15. LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] +
- 16. LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] +
- 17. LRBЧто должно получитьсяТеперь можно и третью строку
- 18. LRBЧто должно получитьсяДалее заполняем по формулам третьи
- 19. LRBЧто должно получитьсяДалее заполняем по формулам третьи
- 20. LRBЧто должно получитьсяДалее заполняем по формулам третьи
- 21. Задача «Черепашка»
- 22. Решение задачи «Черепашка». П.П.Полный перебор вариантов –
- 23. Длительность вычислений
- 24. Решение задачи «Черепашка». Д.П.
- 25. Код (на паскале)
- 26. Вычисление пути
- 27. Вычисление пути
- 28. Сдать можно как задачу №2965Там даже не требуется вывести путьИ идет черепашка в другом направленииhttp://informatics.mccme.ru/mod/statements/view3.php?id=656&chapterid=2965#1
- 29. Задача №619 с восстановлением путиДля считывания на
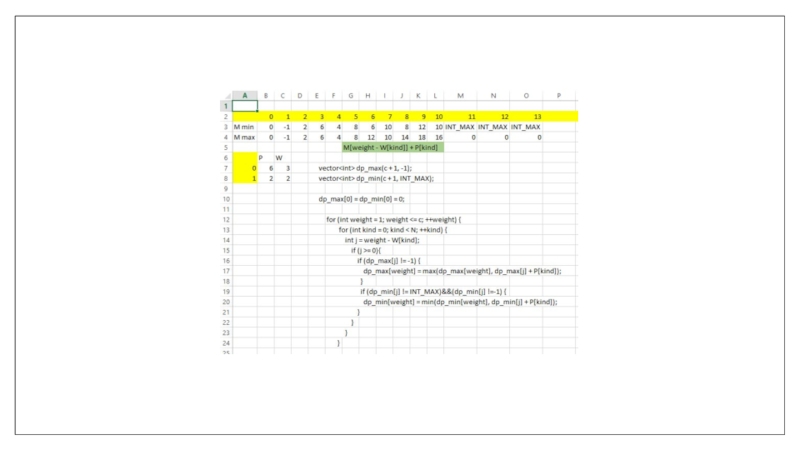
- 30. РюкзакРюкзак без стоимости (камни) № 1119Рюкзак с фиксированным набором вещей № 3089Рюкзак с выводом № 3090
- 31. Задача по ДП про штрафу при удалении
- 32. Её разбор тутhttps://youtu.be/pq4pA8PzP5w
- 33. Копилка (размен, банкомат) № 625Задан вес E
- 34. Слайд 34
- 35. Скачать презентанцию
Задача «Возрастающая подпоследовательность» № 613
Слайды и текст этой презентации
Слайд 6Сдать можно как задачу №613
http://informatics.mccme.ru/mod/statements/view3.php?chapterid=613#1
Слайд 11L
R
B
Что должно
получиться
Первую строку заполняем первой строкой из А
Заполняем вторую
строку B по-честному
Слайд 12L
R
B
Что должно
получиться
Первую строку заполняем первой строкой из А
Заполняем вторую
строку B по-честному
Слайд 13L
R
B
Что должно
получиться
Теперь можно и третью строку В заполнить
B[i, j]
= 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i, j] = L[i-1,j-1] +
B[i,j]R[i, j] = R[i-1,j+1] + B[i,j]
Заполняем вторую строку L и R по формулам
![LRBЧто должно получитьсяТеперь можно и третью строку В заполнитьB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j]](/img/thumbs/302b33ac22d6acf04357ceda8f50352d-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяТеперь можно и третью строку В заполнитьB[i, j] =")
Слайд 14L
R
B
Что должно
получиться
B[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i,
j] = L[i-1,j-1] + B[i,j]
R[i, j] = R[i-1,j+1] + B[i,j]
Теперь
можно и третью строку В заполнить![LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j] = L[i-1,j-1] + B[i,j]R[i, j] =](/img/thumbs/8be7e91e70b06ab930bf1a565e9282c6-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j]")
Слайд 15L
R
B
Что должно
получиться
B[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i,
j] = L[i-1,j-1] + B[i,j]
R[i, j] = R[i-1,j+1] + B[i,j]
Теперь
можно и третью строку В заполнить![LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j] = L[i-1,j-1] + B[i,j]R[i, j] =](/img/thumbs/4aeddcc31299c1e8a706dfc3d9c29682-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j]")
Слайд 16L
R
B
Что должно
получиться
B[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i,
j] = L[i-1,j-1] + B[i,j]
R[i, j] = R[i-1,j+1] + B[i,j]
Теперь
можно и третью строку В заполнить![LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j] = L[i-1,j-1] + B[i,j]R[i, j] =](/img/thumbs/c66d11800518a7db95d6c1bd097d467d-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j]")
Слайд 17L
R
B
Что должно
получиться
Теперь можно и третью строку В заполнить
B[i, j]
= 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i, j] = L[i-1,j-1] +
B[i,j]R[i, j] = R[i-1,j+1] + B[i,j]
![LRBЧто должно получитьсяТеперь можно и третью строку В заполнитьB[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]L[i, j]](/img/tmb/4/328729/31a374b4bc0aa75d908703be054ef3c4-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяТеперь можно и третью строку В заполнитьB[i, j] =")
Слайд 18L
R
B
Что должно
получиться
Далее заполняем по формулам третьи строки L и
R
B[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i, j] =
L[i-1,j-1] + B[i,j]R[i, j] = R[i-1,j+1] + B[i,j]
![LRBЧто должно получитьсяДалее заполняем по формулам третьи строки L и RB[i, j] = 2*B[i-1,j] + L[i-1,j-1] +](/img/thumbs/dfd98a81c046f907e42b75218c2da24b-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяДалее заполняем по формулам третьи строки L и RB[i,")
Слайд 19L
R
B
Что должно
получиться
Далее заполняем по формулам третьи строки L и
R и т.д.
B[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i,
j] = L[i-1,j-1] + B[i,j]R[i, j] = R[i-1,j+1] + B[i,j]
![LRBЧто должно получитьсяДалее заполняем по формулам третьи строки L и R и т.д.B[i, j] = 2*B[i-1,j] +](/img/thumbs/be2036281e0956b169841edc59a76c81-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяДалее заполняем по формулам третьи строки L и R")
Слайд 20L
R
B
Что должно
получиться
Далее заполняем по формулам третьи строки L и
R и т.д.
B[i, j] = 2*B[i-1,j] + L[i-1,j-1] + R[i-1,j+1]
L[i,
j] = L[i-1,j-1] + B[i,j]R[i, j] = R[i-1,j+1] + B[i,j]
![LRBЧто должно получитьсяДалее заполняем по формулам третьи строки L и R и т.д.B[i, j] = 2*B[i-1,j] +](/img/tmb/4/328729/db6a3d84c27e10449154335d2731dc68-800x.jpg "Олимпиадные задачи LRBЧто должно получитьсяДалее заполняем по формулам третьи строки L и R")
Слайд 22Решение задачи «Черепашка». П.П.
Полный перебор вариантов – универсальный способ решения.
Но рассмотрим его потенциальные возможности
Пусть дана таблица 4х4. Любой путь
состоит из трёх перемещений вверх и трех перемещений вправо, т.е. длина пути равна шести. Другими словами, дано 6 шагов, из них 3 выбираются для перемещений вверх, оставшиеся 3 – для перемещений вправо определяются однозначно. Т.о. количество способов выбора трех перемещений из шести При нахождении суммы (стоимости) пути потребуется 5 операци сложения, всего 100 операций. Оценим время решения задачи для компьютера с миллионным быстродействием (см. презентация предыдущих занятий о сложности алгоритмов и быстродействии на примере задачи о тупоугольном треугольнике)
Слайд 28Сдать можно как задачу №2965
Там даже не требуется вывести путь
И
идет черепашка в другом направлении
http://informatics.mccme.ru/mod/statements/view3.php?id=656&chapterid=2965#1
Слайд 29Задача №619 с восстановлением пути
Для считывания на С++ в ней
удобно хранить массив из char и получать цифру, вычитая код
символа ‘0’. Он равен 48, но можно написать прямо так:Как видим, не забыли привести к int полученый код.
Слайд 30Рюкзак
Рюкзак без стоимости (камни) № 1119
Рюкзак с фиксированным набором вещей
№ 3089
Рюкзак с выводом № 3090
Слайд 33Копилка (размен, банкомат) № 625
Задан вес E пустой копилки и
вес F копилки с монетами. В копилке могут находиться монеты
N видов, для каждого вида известна ценность Pi и вес Wi одной монеты. Найти минимальную и максимальную суммы денег, которые могут находиться в копилке.
